Kepler and Kircher on the Harmony of the Spheres

The Harmony of the Spheres, a transdisciplinary idea that unites cosmology, astronomy, mathematics, and music theory, has been a major vehicle of the Pythagorean current in the intellectual history of the West. This article focuses on two figures who contributed largely to it in the early phase of the Scientific Revolution. By learning and inclination, both had come under Neoplatonic and Hermetic influences; both were adherents of that stream of Christian esotericism that sought a deeper understanding of the created world. But as we shall see, their attitudes to celestial harmonies were in stark contrast to one another.

Every book on Johannes Kepler (1571–1630), and most books on the history of astronomy, make mention of the theory of celestial harmony that Kepler developed in Harmonices Mundi (1619).¹ They often reproduce, as a curiosity, his notation of the planetary “songs”:

Figure 1

The importance of this work for the history of science is undisputed. It completed what were later named the three Keplerian Laws of Planetary Motion: 1. Each planet moves in an ellipse with the sun at one focus. 2. The radius vector of each planet passes over equal areas in equal intervals of time. 3. The square of the period of revolution of a planet about the sun is proportional to the cube of the mean distance of the planet from the sun.² Kepler himself was unable to provide a physical explanation for these laws, but they formed the basis for Isaac Newton (1643–1727) to develop his theory of universal gravitation, which confirmed their validity and ensured their discoverer’s immortality.

It was the data of the new astronomy, as contained in the observations and tables of his master Tycho Brahe (1546-1601), that had forced these conclusions on Kepler after many years of intense research and meditation. They necessitated two radical novelties in the arrangement of the solar system: first, the acceptance of the Copernican or heliocentric system; and second, the elliptical orbits with their variable speeds of planetary motion, which abolished the epicycles and equants that cluttered the Ptolemaic or geocentric system. While there were a few precedents for heliocentrism in the ancient world, the second conclusion went against the entire astronomical tradition, and especially against the principle enunciated by Aristotle and accepted by Ptolemy: that everything in the heavens moves in perfect circles. Even Copernicus had not contravened it.

Kepler’s laws “saved the appearances” more successfully than any previous theory, but that was not enough for him, driven as he was by a lifelong passion to discover the divine rationale behind the appearances. Having already justified the Copernican arrangement of the planets around the sun by means of a geometric argument involving the five Platonic solids,³ he now addressed the irregularity of their orbits. Why should God have made these elliptical rather than circular, and so various in their degrees of ellipticality?

In seeking the answers to these questions, Kepler’s basic assumption was the Pythagorean one: that the key to the cosmos lies in number. A secondary idea, equally Pythagorean in origin, was that harmony endows number with meaning, quantity with quality. It privileges certain numbers over others, namely the ones that, translated into musical terms, produce the intervals that we perceive as consonant, pleasant, and musically useful. Harmonices Mundi is a triumph of ingenuity in reading these principles into the data of the new astronomy, and thereby justifying the latter.

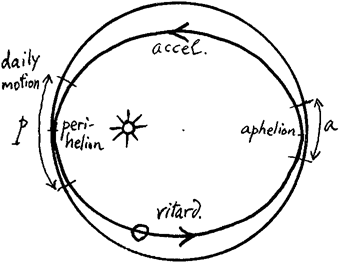
Historians of science are well aware of how Kepler’s argument works, and of the connection between the planetary songs and the First Law, but to some readers it may be helpful to explain it here. In this exaggerated diagram of a planet’s elliptical orbit, its motion is seen to accelerate as it approaches perihelion (nearest to the sun) and to decelerate as it moves away towards aphelion (furthest from the sun).

Figure 2

Following Kepler’s Second Law, its acceleration depends on the degree of ellipticality of its orbit. For example, Mercury’s orbit is much more elliptical than Venus’s, which is almost circular. Therefore the difference between Mercury’s extreme positions is much greater than that of Venus, and the musical interval expressing that difference much wider.

The natural philosophers of antiquity believed that the planets are not silent in their orbits. Setting aside the question of whether they move through air or through some finer medium like ether, it seemed logical that these great bodies should make a sound, just as moving bodies do on earth; and the many theories of the Harmony of the Spheres remain as attempts to specify what that sound could be, translated into the language of music.

There are two main schools of thought as to how this translation should be made. The first one assumes that the relative distances of the planets from the earth relate harmonically, as if they were different points on a string. This theory derives from Pythagoras’s school, in which the distance of the earth from the moon’s sphere was reckoned to be 126,000 stades. Taking this distance as equivalent to a whole-tone, the distances to the other planetary spheres were proportioned like the intervals of a diatonic scale.⁴ The second school holds that it is the motions of the planets that relate harmonically, their different rates of revolution corresponding to differences of pitch. These all presume a stationary and silent earth, though it was not certain whether the revolutions should be calculated relative to the earth, in which case Saturn, having furthest to travel, would move fastest, or relative to the zodiac, in which case Saturn would be the slowest planet, taking 30 years to make one circuit, and the moon, with its cycle of 28 days, the fastest.⁵

There are other schemes, especially those of the Arab astronomers and the various interpreters of the “scale” of Plato’s Timaeus, but they need not concern us here. What results from every scheme prior to Kepler is that the planetary tones are derived from some existing scale or interval-sequence that cannot possibly be valid in any scientific, quantitative way, because the known proportions of either distances or motions are vastly different from the proportions of the tones used to represent them. This is where Kepler’s approach differed from all his predecessors’: his work of 1619 was the first time that a theory of celestial harmony was derived directly from astronomical observation.

Hitherto, these theories had almost unanimously assigned a single, unvarying tone to each planet, as one would expect to result from a perfect circular orbit.⁶ However, with an inspired leap of the imagination Kepler saw that the planetary tones must now vary, their pitch rising and falling in proportion to their acceleration and retardation. He calculated the exact amount by comparing the daily motion of a planet at perihelion with its daily motion at aphelion, expressed as degrees of a circle. This gave a simple proportion, which like all proportions could be translated into musical intervals by regarding the two terms as different string-lengths.

For example, Saturn’s angular motion at aphelion, following Kepler’s data, is 106 minutes of arc. At perihelion, it is 135 minutes. The proportion of the two quantities, 106:135, is approximately 4:5. Two strings of relative lengths 4 and 5 sound pitches a major third apart. Therefore Saturn’s “song” is contained within the limit of a major third (see Figure 1).⁷

The corresponding figures for Jupiter are: motion at aphelion 270 minutes; motion at perihelion 330 minutes. The proportion 270:330 is approximately 5:6, thus its musical interval is a minor third.

In the case of Venus, which has an almost circular orbit, the pitch difference is 24:25, an interval smaller than a semitone which Kepler notates as a unison. In the case of Mercury’s orbit, its musical representation covers an octave plus a minor third (though it is erroneous to assume, as the notation suggests, that its upward and downward courses are different).

Kepler could now satisfy his need to find divine reason in the planetary motions: it was God’s desire that the cosmos should produce a variety of tones and harmonies. With somewhat forced arguments, he found in these both the major and the minor modes, but unfortunately the music of all the planets singing at once was horribly discordant by seventeenth-century standards. Since the six planets hardly ever coincide on the notes of a perfect triad, Kepler tabulated all the cases in which five or even only four of them do so, filling many pages in a desperate attempt to adapt the data to traditional harmony. In fact, his planetary music, when transposed within our range of auditory perception, sounds much more like twentieth-century electronic music, as one can hear from the recording made in 1979 by two professors at Yale University, John Rodgers and Willie Ruff.⁸

None of the believers in the Harmony of the Spheres contended that we can hear it on earth. Tycho Brahe himself, not contesting the existence of the heavenly music, had used our deafness to it as sure evidence that the heavens cannot be filled with air.⁹ Kepler could not leave it at that. Having taken such pains to establish the existence of an entirely new kind of planetary music, he had to integrate it with his search for meaning and purpose in the cosmic ordering: someone, besides God, had to benefit from it. In the final chapter of his book, he refers to Tycho’s surmise that the planets might be inhabited, and suggests that the intellect best able to appreciate the planetary harmonies might reside in the place from which they are measured, namely the Sun. “What use is this furnishing, if the globe is empty? Do not the very senses themselves cry out that fiery bodies inhabit it, which have the capacity for simple minds, and that in truth the Sun is, if not the king, at least the palace of the ‘intellectual fire’?”¹⁰

By modern criteria, Kepler seems to have had a split personality, half scientist, half mystic. His obsession with cosmic harmony puts him in the same category as Robert Fludd, author of Utriusque cosmi historia (1617) and other encyclopedic works of Christian Hermetism; yet in the Appendix to Harmonices Mundi, Kepler attacks Fludd’s system on the grounds that “what he endeavors to teach us as harmonies are mere symbolism...rather than philosophical or mathematical.”¹¹ The immense value of Kepler’s discoveries, to his own way of thinking, was anything but a split: it lay in the fact that his Neoplatonic intuitions were backed up by hard, scientific data.

To his sorrow, they were received in profound silence by the scientific world, in which the Harmony of the Spheres was as irrelevant as the quest for the unicorn. The heliocentrists, Copernicus and Galileo, had ignored the time-honored myth, and it played no part in the rapid triumph of their cosmology. It would take Newton to sift Harmonices Mundi and extract the scientific wheat from the speculative chaff. However, after Kepler’s death his work found one careful reader: Athanasius Kircher (1602-1680), whose combination of a scientific mentality with Christian piety and a Hermetic-Neoplatonic philosophy resembled Kepler’s own.

It is instructive to see these esoteric inclinations occurring across the sectarian divide that separated the heterodox Lutheran¹² Kepler from the Jesuit Kircher, and to compare the consequences of it for our subject. Take first the Copernican question. In his standard history of the Copernican Revolution, Thomas S. Kuhn writes that “Protestant leaders like Luther, Calvin and Melanchthon led in citing Scripture against Copernicus and urging the repression of Copernicans. [...] For sixty years after Copernicus’ death there was little Catholic counterpart for the Protestant opposition to Copernicanism.”¹³ His system was known in the Catholic universities, and his calculations aided in the preparation of the new Gregorian Calendar of 1582. For a while, the Church held no official position on the subject, and free debate prevailed among those able to comprehend the mathematical arguments pro and con. In 1584 Giordano Bruno published his cosmological ideas, including a defence of Copernicus, in his Cena de le Ceneri, and lived, for the time being, unmolested.

Meanwhile, the Lutheran astronomer Tycho had become increasingly dissatisfied with the Aristotelian model of the heavens. His observation of comets had persuaded him that the heavens did not consist of solid, crystalline spheres, but that comets, planets, and the earth all floated in a rarefied ether. This conclusion freed him from dependence on either the Aristotelian-Ptolemaic system or on the Copernican, while his aristocratic and independent nature induced him to invent his own solution. By 1587 he was writing to his correspondent Christoph Rothmann about “a certain theory concerning the arrangement of the heavenly revolutions other than the Ptolemaic or Copernican, far more agreeable than these, and recently ascertained by me, informed by experience itself.”¹⁴

While Tycho’s system was indeed based on his observations, and these of a precision hitherto unequalled, he too subscribed to Neoplatonic notions of a living and harmonious cosmos. He wrote: “As that divine philosophy of the Platonists seems to have appropriately realised, heaven is animated, and the heavenly bodies are themselves animated, endowed with the living spirit of a particular heaven.”¹⁵ He rejected Copernicus’ system, but mainly on aesthetic grounds because he found it ill-proportioned when compared with the ratios, symmetries, and harmonies found in the microcosm. Referring to the heliocentric hypothesis, he says that “That ungeometric, and asymmetric, and disordered way of philosophising would produce something very foreign to divine wisdom and providence.”¹⁶ His own solution, known as the Tychonian system, has the planets revolving around the sun, while the sun, together with the moon and the fixed stars, revolves around an unmoving earth.

It was this cosmology that was eventually adopted by the Society of Jesus, and thus of necessity by Kircher. Originally, the Jesuits had no official position on the matter, except that the Society’s rules required that “In matters of any importance professors of philosophy should not deviate from the views of Aristotle, unless his view happens to be contrary to a teaching that is accepted everywhere in the schools; or especially if his opinion is contrary to the orthodox faith.”¹⁷ Nonetheless, by the early years of the seventeenth century the Society had become one of the Copernican system’s main promoters, albeit unintentionally, because of the excellent astronomical teaching of their colleges in which all systems were studied from a mathematical point of view, even if only to refute them.¹⁸ Jesuit scientists shared in the excitement about the discoveries that Galileo was making through his telescope, such as the four satellites of Jupiter and the phases of Venus, and when in 1611 Cardinal Bellarmine (himself a Jesuit) asked them to evaluate the discoveries, they confirmed them, despite their deviation from Aristotelian orthodoxy.¹⁹

Kepler had long been convinced by Copernicus, and in his Astronomia Nova (1609) could shrug off the objections of his fellow Protestants in the following bold words:

In theology the influence of authority should be present, but in philosophy it is the influence of reason that should be present. St. Lactantius denied that the earth is round; St. Augustine conceded its roundness but denied the antipodes; today the Holy Office concedes the smallness of the earth but denies its motion. But for me the holy truth has been demonstrated by philosophy, with due respect to the Doctors of the Church, that the earth is round, that its antipodes are inhabited, that it is quite despicably small, and finally that it moves through the stars.²⁰

This was exactly the kind of attitude that led, under the Catholic hegemony, to the prohibition placed upon Galileo in 1616, not to “hold or teach” the Copernican system. As is generally acknowledged by scholars today, it was not because the geocentric system was official dogma, but because Galileo, as a layman, had presumed to interpret the Bible and the Church Fathers as suited his scientific program. Rivka Feldhay, in her useful summary of the “Trials” of Galileo, writes that from the point of view of the church authorities, “an attempt to prove the motion of the earth might result in an encroachment on the domain of scholastic philosophers and theologians, who, in fact, had been unchallenged by the traditional form of astronomy. It could also be perceived as a threat to the monopoly of priests in the interpretation of the Scriptures which the decrees of the Council of Trent for the first time had anchored in canon law.”²¹

The prohibition had the immediate effect of placing Copernicanism itself under a ban in Catholic lands. The General of the Jesuits, Claudio Aquaviva (1543–1615) had already been tightening the screws on the Order’s members to enforce Aristotelian and Thomist orthodoxy.²² After the prohibition of 1616, the Jesuit scientists had to find some non-Copernican system within which to work, and the Tychonian, which had room for recent discoveries but did not require a re-interpretation of the Scriptures, was the best they could find.

This was not a happy situation for the scientists, and its consequences are starkly summed up in the words of Robert Blackwell: “Jesuit science thus died on the vine, just as the first blossoms appeared.”²³ Blackwell writes of the typical predicament of Orazio Grassi (1583–1654), who held the Chair of Mathematics at the Collegio Romano (the Jesuit college in Rome), and who had had a long controversy with Galileo:

As an informed astronomer he knows that the Aristotelian-Ptolemaic hypothesis is beset with serious difficulties; as a Jesuit he knows that the Church’s condemnation of Copernicanism obliges him under religious obedience to accept the qualification that the Copernican hypothesis is erroneous. So just three years after the condemnation, Grassi turned to the Tychonic model as a compromise — a reaction which he shared with many other Jesuit astronomers at the time.²⁴

This, then, was the system that Athanasius Kircher was obliged to adopt in his published works, whatever he thought in private:²⁵ a constriction that would naturally affect any theory he might have on the Harmony of the Spheres. In his early work on optics, Ars Magna Lucis et Umbrae (1646), Kircher outlines philosophical principles hardly different from Kepler’s. Celestial bodies (he writes) are placed by the Creator to complement discord with concord, consonance with dissonance, and sometimes to give absolute harmony. (This is exactly what Kepler found in combining the planetary songs.) As we see, the sun encourages growth and procreation, then in the autumn when it retires, things decay. But God has put the moon there to perform twelve circuits to each one of the sun, and to supplement the want of sunlight. The combination of influences is responsible for all the generation in our world.²⁶ “For the same reason, the rest of the planets have various courses, aspects, and anomalous movements relative to the earth and the sun, so that by their approach and departure from the sun, moon, and earth, and by the various mixtures of light and qualities, they cause various effects here below.”²⁷

Towards the end of Ars Magna Lucis, Kircher draws up a chart, based on data from Tycho Brahe’s observations and conjectures about the distances of the planets from the sun and from the earth, and his estimates of the diameters of the planets and the sun.²⁸ This was bound to give different figures from Kepler’s elliptical orbits and heliocentric system, but the most notable thing about the chart is its emphasis on proportion. Kircher tabulates the proportions of the earth’s radius to the radii of the sun, moon, and planets; the proportions of the earth’s volume to the volumes of the same; and the proportions of the sun’s diameter to the radii²⁹ of the planets.

In the sciences of the classic Quadrivium (Arithmetic, Geometry, Music, and Astronomy), proportion is studied in the context of musical intervals, and consequently, proportional tables immediately put one in mind of intervallic studies. What leaps out of this chart is that the great majority of the proportions give non-harmonic intervals, not used in the musical system.³⁰ There is no possibility of deriving a theory of the Harmony of the Spheres from them, and Kircher perhaps intended to show the absurdity of any such attempt.

Kepler’s harmonies receive specific attention in Kircher’s encyclopedic work on music, Musica Universalis (1650), whose tenth and last book, “Decachordon Naturae,” promises to demonstrate “that the nature of things in all respects observes musical and harmonic proportions, and that even the nature of the universe is nothing other than the most perfect music.”³¹ Introducing the theme of the Harmony of the Spheres, Kircher writes that many have tried to specify the celestial harmonies, but that all their efforts are flawed.³² Yet according to Pythagoras, Seneca, Saint Augustine, Cicero, Plato, Philo, Boethius, and many others, the world must be harmonious; or (to draw on Kircher’s favored metaphor), if the universe is the Temple of God and the Church of the Blessed, then it cannot lack for singers and organs.³³

Modern astronomy, Kircher continues, has exploded the ancient belief that the celestial bodies make audible harmony, since the heavens have no solidity, nor is the order of the spheres the same as the ancients thought. Having thus dismissed the ancients, he turns to Kepler, who replaced Ptolemy’s theories with a new structure of the heavens, yet wrapped it in almost unintelligible, mystical terms. Kircher summarizes Kepler’s theory of the Platonic solids as dictating the planetary orbits, with a diagram, and concludes “I truly do not see how the intended harmony of the heavens can be proven from these [speculations] by Philosophers and Mathematicians, since one could rather say that the heavens are forced into his violently distorted five solid bodies, than that the bodies are applied to the heavens.”³⁴

It was the inaccuracies in Kepler’s scheme that displeased Kircher, as indeed it had displeased Kepler, who, finding that the orbits did not fit perfectly between the five solids, was set on the path that led to the solutions of Harmonices Mundi. Turning to the latter, Kircher reproduces Kepler’s astronomical data and the “songs” derived from them, but refuses to grant that the proportions between perihelion and aphelion motion deserve to be called harmonic. They are simply not accurate enough. Saturn’s proportion of 135:106 is not a major third, says Kircher; that would require the latter figure to be 108. For Jupiter’s interval to be a minor third, its proportion should be not 270:330 but 270:324. In short, there are no perfect consonances in Kepler’s data.

Kircher passes from Kepler’s theories to those of the Bohemian astronomer Anton Maria Schyrleus de Reita, which need not concern us here.³⁵ He then tells his readers what the heavenly harmony really consists of. (Because of Kircher’s verbose writing, I give a précis³⁶ rather than a complete translation.) The heavenly harmony (he says) cannot be shown in numbers of motions or the sensible collision of heavenly bodies, but only in their admirable disposition, and their ineffable proportion one to another, so that to take one away would cause the whole to perish. It is also in the exact quantity and magnitude of each body for achieving the desired effect. Thus the sun, moon, and earth have the requisite distances and magnitudes for perfect mutual influence, aid, and preservation. (Kircher gives no figures for any of these.) An example is the temperature on the earth, ideal for human life which would be impossible if the sun were closer or further away.

The distances between the sun, earth, and planets are such as to balance the sun’s heat with the moon’s coldness. For example, in summer the sun is strong, the moon weak, causing a variety and mixture of consonance and dissonance. The influence of the sun and moon is like a perfect octave. However, God has added Venus to give support with virtues such as vary the lunar influences; meanwhile, Mercury modifies that which is noxious in the sun. The changing distances from the earth bring about different effects.

Moreover, God has placed two dissonant bodies, Mars and Saturn, from whose pestiferous evaporations all the earth’s ills come. Yet between them is the benign star of Jupiter. The malefic planets act like caustic medicines which attract sick matter and liberate it, so that there is no ill in nature that does not turn to good.

In musical terms, Mars and Saturn are dissonances, tied in perfect syncopation to Jupiter, while Mercury sounds a dissonance between the concords of Venus and the moon. The seven planets together give a perfect “tetraphony” or four-part harmony that Kircher now illustrates with a short musical example:

Figure 3

This trivial phrase may compare poorly with Kepler’s spectacle of ever-changing harmonies, but perhaps it was deliberately poor, just as the tables of proportions in Ars Magna Lucis were conspicuously un-harmonic: they showed, as Kircher undoubtedly believed, that the heavenly harmonies could not possibly be reproduced in earthly music.

The solar system of Kircher’s day had become much more complex than the seven traditional planets. Although Uranus, Neptune, and Pluto still lay undiscovered, the primitive telescope had revealed four moons around Jupiter, and twin bulges or adjacent satellites (actually, the rings) of Saturn. Wanting to find a rationale for these phenomena, Kircher hit on the idea that the heavenly bodies were grouped in “choirs.” The outermost one was the Choir of Saturn, in which the planet was given two “moons” to supplement the light of the distant sun. Next came the Choir of Jupiter, the only instance in which Kircher offers a harmony based on astronomically determined numbers. According to Reita’s figures, Jupiter’s moons were distant by 3, 4, 6, and 10 diameters of their planet. “Whatever is requisite for music certainly lies concealed in these numbers: for the distances of each body correspond precisely to a harmonic quantity: 3:4:6:10.”³⁷ But the real purpose of the “Jovian Choir” was to cast an ever-changing variety of light and shade and thus to moderate the influences that Jupiter sends down to our world. Then there is the “The Solar or Apolline Choir,” which “contains in itself Venus, Mercury, the moon, the earth, and is parallel, as it were, to the Jovian Choir; of which enough has been said at the beginning, so we will not repeat it here.”³⁸ The one planet left out of any choir is Mars, whose eccentric orbit carries it now close to Jupiter, now to the sun, bringing to each its “syncopations” and baleful influences.

To deter those who might suspect other purposes in such a complicated arrangement, Kircher draws a “corollary” that seems directly aimed at Kepler’s bold speculations about other inhabited spheres:

Some say that in places where men are unable to dwell because of the excessive intensity of the light, or because of temperatures incompatible with human nautre, there are creatures endowed with a different nature. Since nothing of the kind is known to us, nor can be known, it seems to be fundamentally dangerous to the Faith. Who could regard it otherwise than as a blind and baseless imagination, a novelty and fiction of sectaries?³⁹

Kircher’s vision of a harmonious cosmos was second to none in its elaboration and imaginative power, of which I have given only a slight sampling here; but whereas Kepler had presented his planetary songs as factual, Kircher’s choirs were mere figures of speech, his “Decachord of Nature” a metaphor for the Hermetic principle of correspondences that he believed to underlie all of creation.

In conclusion, I will mention some of the later developments of Kepler’s and Kircher’s ideas. Kepler’s faith in an astronomical rationale for the Harmony of the Spheres lay latent for nearly three centuries, until with the dawn of the twentieth century a few isolated researchers began reconsidering it. The first of these was Emile Abel Chizat (1855–after 1917), a French composer and impresario.⁴⁰ His approach consisted in a revision of the first type of planetary music, as described above, which compares the planetary distances to intervals on a hypothetical string. Unlike the Greek and medieval theorists, whose musical system was limited to two or three octaves, Chizat found that it took over seven octaves to notate the intervals of the planets from Mercury to Neptune, including the asteroids Hungaria, Vesta, Ceres, Psyche, and Ismene, and to discover that they fell into place in a gigantic major chord.

I will only mention briefly the theories of some other twentieth-century researchers: W. Kaiser, who found harmonies not in the distances between the planets, as Chizat did,⁴¹ but in their mean distances from the sun; Alexandre Dénéréaz, who constructed a scale based on taking the Golden Section of the planetary distances;⁴² Rodney Collin, who used as his data the conjunctions of the planets;⁴³ Thomas Michael Schmidt, who derived significant (musical) harmonies by comparing the time-periods of the planets’ rotation around the sun.⁴⁴ More relevant to this study are those who addressed themselves specifically to Kepler’s harmonies.

In 1909 Ludwig Günther revisited Harmonices Mundi, corrected Kepler’s values according to modern astronomy, and applied their principle to Uranus and the asteroids Ceres, Vesta, Pallas, and Juno.⁴⁵ This exercise was completed by Francis Warrain in his book on Kepler, published in 1942, which included the perihelion and aphelion values for Neptune (discovered 1843) and Pluto (1930).⁴⁶ Finally, Warrain’s data were analyzed by Rudolf Haase following the methods of Hans Kayser, the re-founder of the science of Harmonics in modern times.⁴⁷ Haase took the aphelion value of Saturn as the fundamental of a theoretical harmonic series, and related all the other values to it in terms of the tones to which they corresponded, irrespective of octave displacements. He found that the great majority of them fell on the tones C, D, E, and G, thus validating the belief that the planetary orbits accord with the laws we know as harmonic. Haase’s approach to the data, and the conclusions he draws from it, are quite different from Kepler’s, expressed as they are in secular and scientific terms and free from the anachronistic influences of musical practice, but they show the continuing vigor of Kepler’s example.

These scattered instances pale in comparison with the recent publishing campaign of John Martineau (born 1967). His books, illustrated with finely-drawn geometrical diagrams, present a mass of evidence that the solar system is in fact designed in accordance with the principles sensed by Pythagoras, the Platonists, and especially Kepler.⁴⁸ For instance, in The Harmony of the Spheres Martineau shows that Kepler was right in principle, both in his interpretation of the planetary orbits as governed by simple geometrical figures and in his conviction that simple musical proportions control their orbits; only these principles need to be tested against contemporary astronomical data, whereupon they prove far more fruitful and accurate than they ever were in the past. A Book of Coincidence collects an astounding number of instances of the geometrical and harmonic placement and interrelation of the planets, any one of which might be dismissed as coincidence, but which, taken as a whole, confirm that, in Plato’s words, “God always geometrizes.”⁴⁹

Kircher would have been delighted by these discoveries. While renouncing the attempt to transcribe the heavenly music in earthly terms, he readily embraced it as a metaphor for the intelligent design of creation. Whereas Kepler’s God had taken delight in assembling a cosmos out of geometric solids and making music out of its motions, Kircher’s God was more a scientist than an artist or musician, calibrating the planetary motions and distances in exactly the right proportions to facilitate life on earth. Concord and discord were merely the musical equivalent of benefic and malefic planetary influences; harmony, of the indescribable complexity and ultimate benevolence of God’s design. These principles, as Kircher believed, could survive any revision of the figures, and even stand aloof from the debate over the Copernican system, of which he himself was a dutiful opponent.

Such an attitude to the Harmony of the Spheres, even if excluded from scientific discourse, served as a fruitful metaphor for three centuries of poets.⁵⁰ And this was not the end of it. In the 1990s, Kircher’s notion of the finely-calibrated earth resurfaced among a few influential biologists, already leaning towards the “Anthropic Principle” (that the only universe we can know is one that happens to contain humans), and to “Gaia Theory” (that the earth is best studied as if it were itself a living organism).⁵¹ They observed that the presence and variety of the biosphere depends on a delicate equilibrium of earth’s characteristics, such as its distance from the sun, gravity, atmosphere, oxygen, water, ocean salinity, axial inclination, presence of the moon, etc. If any of these were even slightly different, life could not have evolved as it has done: a situation playfully christened “The Goldilocks Effect.”⁵² For Kircher, this could only be the work of a concerned, personal God, and its sole purpose was to serve man, whose purpose in turn was to serve and love God. Today’s scientists prefer non-theistic explanations, but the phenomenon of earth’s fine-tuning remains as a challenge to cosmologists, who may find themselves unwittingly continuing where Kepler and Kircher left off.