Quantum Reality

BEYOND THE NEW PHYSICS

Nick Herbert

ANCHOR PRESS/DOUBLEDAY

Garden City, New York

Preface

One of the curious features of modern physics is that in spite of its over-
whelming practical success in explaining a vast range of physical phenom-
ena from quark to quasar, it fails to give us a single metaphor for how the
universe actually works. The old mechanical metaphor "The world is a
giant clock" condensed in one image the principal features of Newtonian
physics—namely, atomicity, objectivity, and determinism. However, phys-
icists today do not possess a single metaphor that unites in one image the
principal features of quantum theory. The main purpose of Quantum
Reality is to examine several tentative images of the world proposed by
quantum physicists.

The search for a picture of "the way the world really is" is an enterprise
that transcends the narrow interests of theoretical physicists. For better or
for worse, humans have tended to pattern their domestic, social, and
political arrangements according to the dominant vision of physical real-
ity. Inevitably the cosmic view trickles down to the most mundane details
of everyday life.

In the Middle Ages, when virtually everyone believed the world to be
the personal creation of a divine being, society mirrored the hierarchy that
supposedly existed in the heavens. Dante's picture of this world as a series
of concentric spheres—heaven the largest; next, the planets' crystalline
spheres; down through our Earth's concentric "elements," the whole sup-
ported by the seven circles of hell—gave everything and everyone his
proper place in the medieval scheme of things, from the divine right of
kings down to the abject obedience of the lowliest serf. Most people
accepted this hierarchical structure without question because it repre-
sented the way the world really is.

The Newtonian revolution toppled the reign of the crystal spheres and
replaced it with a physics of ordinary matter governed by mathematical
laws rather than divine command. Coincident with the rise of Newtonian
physics was the ascent of the modern democracy which stresses a "rule of

laws rather than men" and which posits a theoretical equality between the
parts of the social machinery. The Declaration of Independence, for ex-
ample, "We hold these truths to be self-evident" reads more like a mathe-
matical theorem than a political document. As above, so below. The egali-
tarian mechanism that Newton discovered in the heavens has insinuated
itself into every aspect of ordinary life. For better or for worse, we live
today in a largely mechanistic world.

Just as Newton shattered the medieval crystal spheres, modern quan-
tum theory has irreparably smashed Newton's clockwork. We are now
certain that the world is not a deterministic mechanism. But what the
world is we cannot truly say. The search for quantum reality is a search for
a single image that does justice to our new knowledge of how the world
actually works.

Many aspects of quantum theory are public knowledge, such as the
notion that all elementary events occur at random, governed only by sta-
tistical laws; that there is a "least thing that can happen"—Max Planck's
irreducible constant of action; and that Heisenberg's famous uncertainty
principle forbids an accurate knowledge of a quantum particle's position
and momentum. A successful quantum reality would incorporate this
knowledge, and much more, into a single comprehensive metaphor for the
way the world really is.

I first encountered the quantum reality question in graduate school
when I learned to describe the behavior of atoms, molecules, and elemen-
tary particles in the mathematical language of quantum theory. Quantum
theory is peculiar in that it describes a measured atom in a very different
manner than an unmeasured atom.

The measured atom always has definite values for its attributes (such as
position and momentum), but the unmeasured atom never does. Every
atom in the world that's not actually being measured possesses (in the
mathematical description at least) not one but all possible attribute values,
somewhat like a broken TV set that displays all its channels at the same
time.

Of course I wondered what sort of reality this strange symbolization of
the unmeasured world actually stood for. Were the attributes of unmea-
sured atoms multivalued, fuzzy, nonexistent, or simply unknown?

However, when I asked my teachers what quantum theory actually
meant—that is, what was the reality behind the mathematics—they told
me that it was pointless for a physicist to ask questions about reality. Best
to stick with the math and the experimental facts, they cautioned, and

stop worrying about what was going on behind the scenes. No one has
expressed physicists' reluctance to deal with quantum reality better than
Richard Feynman, a Nobel laureate now at Cal Tech, who said, "I think it
is safe to say that no one understands quantum mechanics. Do not keep
saying to yourself, if you can possibly avoid it, 'but how can it be like that?'
because you will go 'down the drain' into a blind alley from which nobody
has yet escaped. Nobody knows how it can be like that."

For the sake of having something in mind while I did my quantum
calculations, I imagined that an atom always possessed definite values for
all its attributes (just like an ordinary object) whether that atom was
measured or not. However, the process of measurement disturbs the atom
so profoundly that its measured attributes bear only a statistical relation to
its unmeasured attributes. I felt sure that such a "disturbance model" of
measurement was capable of accounting for quantum randomness, the
Heisenberg uncertainty relations, and other quantum mysteries as well. In
this "disturbance" picture, an atom's actual position and momentum are
always definite but usually unknown; its measured position and momen-
tum cannot be accurately predicted because the measuring device neces-
sarily changes what it measures.

My belief in this disturbance model of reality was strengthened when I
read that young Werner Heisenberg once held a similar view of the quan-
tum world. It did not occur to me to wonder why Heisenberg quickly
abandoned such an obvious explanation to take up the more obscure and
mystical Copenhagen interpretation, which most physicists endorse today.

In brief, the Copenhagen interpretation holds that in a certain sense
the unmeasured atom is not real: its attributes are created or realized in
the act of measurement.

I regarded the Copenhagen interpretation as sheer mystification com-
pared to the clarity and common sense of my disturbance model. Blissfully
ignorant concerning the real issues surrounding the quantum reality ques-
tion, I got my degree and continued my career as an industrial and aca-
demic physicist.

In the summer of 1970 my friend Heinz Pagels, a physicist at Rockefel-
ler University, showed me a paper published in an obscure new journal.
"Here's something strange that should interest you, Nick," he said. This
strange new thing was Bell's theorem, a mathematical proof which puts
strict conditions on any conceivable model of reality, quantum or other-
wise.

Bell's theorem is easy to understand but hard to believe. This theorem

says that reality must be non-local. "Non-local" means, in terms of my
disturbance model, that the atom's measured attributes are determined
not just by events happening at the actual measurement site but by events
arbitrarily distant, including events outside the light cone—that is, events
so far away that to reach the measurement site their influence must travel
faster than light. In other words, when I probe an atom's momentum with
a momentum meter, its true momentum is disturbed, according to Bell's
theorem, not just by the momentum meter itself but by a vast array of
distant events—events that are happening right now in other cities, in
other countries, and possibly in other galaxies. According to John Bell, the
act of measurement is not a private act, but a public event in whose details
large portions of the universe instantly participate.

Bell's theorem is a mathematical proof, not a conjecture or supposition.
That is, once you accept a few simple premises his conclusion certainly
follows. Thus Bell does not merely permit or suggest that reality is non-
local; he actually proves it.

Bell's theorem has immensely clarified the quantum reality question.
For instance we now know for certain that no local model (such as my
naive disturbance model) can explain the quantum facts. Bell's theorem
has important consequences for all models of quantum reality including
the Copenhagen interpretation, and its effects continue to reverberate in
physics circles. This book explores various quantum realities (models of
the world consistent with quantum theory) in the light of Bell's important
discovery.

Many people have helped me in my search for quantum reality, either
through their books and articles or through personal contact. I can men-
tion only a few but I'm grateful to all.

I would like to honor the memory of Randy Hamm, friend and talented
animator whose collaboration on Benjamin Bunny Faces Reality, an unfin-
ished animated film which explores some of the same concepts contained
in this book, inspired me to think in new directions.

I would like to thank Mike and Dulce Murphy for opening Esalen
Institute, Big Sur, to physics conferences on quantum reality. Thanks also
to the many participants in the Esalen conferences, especially Henry
Stapp, Saul-Paul Sirag, John Clauser, David Finkelstein, John Cramer,
Larry Bartell, H. Dieter Zeh and Bernard d'Espagnat, from whom I re-
ceived much enlightenment concerning the quantum mysteries.

Thanks to Charles Brandon and The Reality Foundation for encourage-
ment and a timely graphics grant, to Lynn Miller for her skillful illustra-

tions, to Shirlee and David Byrd for editorial assistance, and to
Doubleday's Phil Pochoda, Dave Barbor, and Chauey Bennetts for their
patience and good advice.

Thanks to my wife Betsy and son Khola for keeping me awake and
aware of other extraordinary realities.

1 - The Quest for Reality

"The essential point in science is not a complicated mathematical
formalism or a ritualized experimentation. Rather the heart of sci-
ence is a kind of shrewd honesty that springs from really wanting
to know what the hell is going on!"

---Saul-Paul Sirag

When I was six my parents gave me a set of children's books—fourteen
orange, black, and gold bound volumes of stories, games, and songs. Sci-
ence was Volume 12, the only book without text, containing instead doz-
ens of black-and-white photographs of big machines and unusual natural
phenomena. One picture in particular fascinated me; recalling it today
still makes me shiver. This picture showed a nest of eggs. But hatching out
of these eggs were baby snakes.

This disturbing photo brought together in one image my vague fears
that beneath the surface of commonplace things lurks an utterly strange
i probably sinister) reality.

Many years later I experienced that same feeling—a lightning realiza-

tion that this world is not what it seems—precipitated not by a picture in
a children's book but by a mathematical argument in a physics journal.
Bell's theorem is a simple but powerful proof concerning the structure of
physical reality, and had the same effect on my imagination as that snake's
nest. Bell's theorem is one of the clearest windows that physicists possess
into the nature of deep reality. I invite you in Chapter 12 to look through
this window too.

Physicists are interested in how the world is put together—out of what
sorts of basic objects, interacting via what sorts of basic forces. Physics
began in antiquity as a kind of natural history, a folk museum of unex-
plained marvels and peculiar facts laid out in haphazard fashion: the world
as lore, direct observation scrambled up with fantastic travelogue, with
medieval bestiaries and alchemical recipes.

In the seventeenth century Galileo, Newton and other natural philoso-
phers discovered that an enormous body of physical facts could be encom-
passed in a few mathematical formulas. For instance with only three math-
ematical laws Newton could explain all motion in heaven and on Earth.
Why should mathematics, developed primarily to keep track of human
business transactions, have anything at all to do with the way the non-
human world operates? Nobel laureate Eugene Wigner refers to this magi-
cal match between human mathematics and non-human facts as "the
unreasonable effectiveness of mathematics in the natural sciences." "This
unreasonable effectiveness," writes Wigner, "is a wonderful gift which we
neither understand nor deserve."

Although mathematics originates in the human mind, its remarkable
effectiveness in explaining the world does not extend to the mind itself.
Psychology has proved unusually resistant to the mathematization that
works so well in physics.

The German philosopher Immanuel Kant was deeply impressed by
Newton's mathematical method and sought to explain its success as well
as to understand its limitations. Kant began his analysis by dividing knowl-
edge into three parts: appearance, reality, and theory. Appearance is the
content of our direct sensory experience of natural phenomena. Reality
(Kant called it the "thing-in-itself") is what lies behind all phenomena.
Theory consists of human concepts that attempt to mirror both appear-
ance and reality.

Kant believed that the world's appearances were deeply conditioned by
human sensory and intellectual apparatus. Other beings no doubt experi-
ence the same world in radically different ways. Scientific facts—the ap-

pearances themselves—are as much a product of the observer's human
nature as they are of an underlying reality. We see the world through
particularly human goggles. Kant felt that the participation of human
nature in the creation of appearances explained both the remarkable abil-
ity of human concepts to fit the facts and the natural limits of such
abilities.

Our concepts appear to match the facts, according to Kant, because
both facts and concepts have a common origin—the human condition.
Insofar as human nature is entwined with the appearances, human con-
cepts will be successful in explaining those appearances. Because we can
only explain those aspects of the world which we ourselves bring to it, the
nature of deep reality must remain forever inaccessible. Man is fated to
know, either directly or through conceptualization, merely the world's
appearances and of these appearances only that part which is of human
origin■

Kant's position is an example of the pessimistic pole of reality research,

which might be expressed this way: human senses and intellectual equip-
ment evolved in a biological context concerned mainly with survival and
reproduction of humankind. The powers that such clever animals may
possess are wholly inadequate to picture reality itself, which belongs to an
order that utterly transcends our domestic concerns.

On the other hand, reality researchers of an optimistic bent argue that
since humans are part of nature, deeply natural to the core, nothing pre-
vents us from experiencing or conceptualizing reality itself. Indeed some
of our experiences and/or some of our ideas may already be making con-
tact with rock-bottom reality.

Besides the optimism/pessimism split, another difference separates re-
searchers into the nature of reality: the pragmatist/realist division. A prag-
matist believes only in facts and mathematics and refuses in principle to
speculate concerning deep reality, such questions being meaningless from
his point of view. Sir James Jeans, the distinguished physicist and astrono-
mer, sums up this pragmatic orientation: "The final truth about a phe-
nomenon resides in the mathematical description of it; so long as there is
no imperfection in this, our knowledge of the phenomenon is complete.
We go beyond the mathematical formula at our own risk; we may find a
model or picture which helps us understand it, but we have no right to
expect this, and our failure to find such a model or picture need not
indicate that either our reasoning or our knowledge is at fault. The making
of models or pictures to explain mathematical formulas and the phenom-
ena they describe is not a step towards, but a step away from, reality; it is
like making graven images of a spirit."

A realist, on the other hand, believes that a good theory explains the
facts because it makes contact with a reality behind those facts. The major
purpose of science, according to the realists, is to go beyond both fact and
theory to the reality underneath. As Einstein, the most famous realist of
them all, put it, "Reality is the real business of physics."

The pragmatist treats his theory like a cookbook full of recipes which
are useful for ordering and manipulating the facts. The realist sees theory
as a guidebook which lays out for the traveler the highlights of the invisi-
ble landscape that lies just beneath the facts.

Most physicists are complex mixtures of pragmatist and realist, at once
both optimistic and pessimistic about their chances for making solid con-
tact with deep reality. Like many other human enterprises, the practice of
science requires a constantly shifting balance between extremes, a sensitiv-
ity to the middle way, as French experimentalist Jean Perrin put it, "be-

tween the instincts of prudence and audacity necessary to the slow prog-
ress of human science."

I do not wish to get specific about what might be meant by "reality
itself" lest we hamper our search with needless preconceptions. Like the
solution to a puzzle or cryptogram, contact with deep reality will no doubt
carry its own validation: we'll know it when we see it. However, as an
illustration of the kinds of realities we might be looking for in physics, I
review here two case histories: the stories of a reality that failed and a
reality that succeeded.

The Luminiferous Ether

In 1864 Scottish physicist James Clerk Maxwell discovered the basic equa-
tions that govern electricity and magnetism. To everyone's surprise these
phenomena turned out to be two aspects of a single entity—the electro-
magnetic field. Today physicists are seeking for a way to unify all of na-
ture's fields. Maxwell was the first physicist to show that the task of field
unification is not futile.

A theoretical bonus which Maxwell reaped from his fusion of two fields
into one was the discovery that waves in his electromagnetic field traveled
at the same speed as the measured velocity of light. On the basis of this
numerical coincidence, Maxwell conjectured that light, in reality, was an
electromagnetic vibration at a particular frequency. The experimental pro-
duction by Heinrich Hertz of low-frequency electromagnetic radiation
(radio waves) which were identical in all respects save frequency to light
confirmed Maxwell's bold conjecture.

All known waves vibrate in some medium (such as air or water). The
medium in which light presumably travels was dubbed the "luminiferous
ether." Late nineteenth-century physicists gave top priority to research
into the ether's mechanical properties. Maxwell described the subject of
this research in these words: "Whatever difficulties we may have in form-
ing a consistent idea of the constitution of the ether, there can be no
doubt that the interplanetary and interstellar spaces are not empty but are
occupied by a material substance or body, which is certainly the largest,
and probably the most uniform body of which we have any knowledge."

From light's well-known attributes one could infer many of this hypo-
thetical ether's properties. For instance, since light travels so fast the
elasticity of the ether must be enormous, millions of times more resilient

than the hardest spring steel. Since light is a transverse wave—vibrating
sidewise rather than back and forth—the ether must be a solid. Gases and
liquids can support only back-and-forth vibrations (sound is an example),
while solids transmit both kinds of vibration (earthquake waves, for exam-
ple, vibrate in all directions). The fact that light vibrates only sidewise (no
back-and-forth light has ever been observed) had to be explained by com-
plex structures in the ether which suppressed altogether this otherwise
natural back-and-forth vibration but which permitted sidewise vibrations
to propagate with extreme rapidity.

Although the universe was filled with a transparent "glass" much harder
than steel, this glass offered not the slightest resistance to the passage of
material bodies. The Earth's motion was seemingly unaffected by the
presence of the luminiferous ether. Some physicists proposed that the
ether might act like a solid for rapid motions such as light, but like a fluid
for slow motions, such as planets, in the manner of certain waxlike solids
with deformation-rate dependent viscosities. In modern terms, such a hy-
pothesis amounts to assuming that the universe is filled brim to brim with
a kind of Silly Putty.

In 1887 two American physicists performed a simple experiment whose
purpose was to determine the velocity of the Earth through this ever-
present vibrating solid. Albert Abraham Michelson and Edward Williams
Morley set up a kind of optical racetrack that pitted a light beam moving
north and south between parallel mirrors against an east/west beam. De-
pending on the direction of the "ether wind," one or the other of these
beams had the track advantage and was sure to win. The result of the
Michelson-Morley experiment was always a photo finish. Despite the
enormous velocity of the Earth through space, a velocity that constantly
changes its direction during the year, the two experimenters could detect
no movement whatsoever of the luminiferous ether past the Earth.

Michelson and Morley's failure to detect the "ether wind" led physi-
cists to propose that massive bodies such as the Earth trap the ether and
carry it along with them. However, attempts to detect this "ether drag"
near massive rotating bodies in the laboratory were unsuccessful. Ether
drag should also distort the apparent positions of distant stars, an effect
which was also noticeably absent.

To explain the failure of Michelson and Morley to detect an "ether
wind," even more preposterous effects were invoked. Dutch physicist
Hendrik Antoon Lorentz and Irish physicist George Francis FitzGerald
independently proposed that motion through the ether resulted in a tiny

contraction of all physical bodies in the direction of motion. The Lorentz-
FitzGerald contraction—a kind of "ether squeeze"—could not be directly
observed, because measuring rods also supposedly shrank when oriented in
the ether wind's direction. The sole function of the Lorentz-FitzGerald
contraction was to even the odds in the Michelson-Morley optical race-
track: the light beam that would have lost the race, by virtue of the L-F
contraction would now travel a shorter path, and consequently both beams
would reach the finish line at precisely the same time. This hypothetical
"ether squeeze" was a desperate attempt to save appearances by loading
the already peculiar ether with yet one more unusual attribute.

Although its properties grew more preposterous with each new investi-
gation, the existence of the ether itself was never called into question. One
of England's leading physicists, the eminent William Thomson, Lord
Kelvin, expressed physicists' general attitude a few years after the Michel-
son-Morley experiment when he said, "One thing we are sure of, and that
is the reality and substantiality of the luminiferous ether."

Despite physicists' strong faith in the existence of the luminiferous
ether, a few years after Lord Kelvin's profession of belief the ether was
swept away into the junkyard of obsolete physical concepts in company
with phlogiston, caloric, and the fabled philosopher's stone.

Albert Einstein, an unknown clerk in the Zurich patent office, pub-
lished in 1905 a new theory of space and time which came to be called the
special theory of relativity. The cornerstone of Einstein's theory was that
only relative motions were of any consequence for the basic laws of phys-
ics. According to Einstein, there is no physical means by which one can
observe a body's absolute motion through space.

Einstein's innocent assumption had far-reaching experimental conse-
quences. For instance, two observers in relative motion measuring the
positions and times of the same events would get different results. For
Einstein, time and space are relative concepts, different for every observer.
Another important consequence of relativity is the famous E = mc2 rela-
tion, which predicts that an object's mass is equivalent to a certain
amount of energy, with an enormous conversion factor—the square of the
speed of light.

Although space, time, and motion are relative concepts in Einstein's
theory, certain other physical quantities are absolute—the same for every-
one. Einstein's major insight, the key to relativity theory, is that all valid
physical laws must be built from these absolute quantities alone. Only in
this way can these laws be made the same for all observers.

One of Einstein's absolutes is the speed of light: it is the same for an
observer on Mars as an observer on Earth. Another Einsteinian absolute is
the so-called space-time interval. Although space and time by themselves
are different for each observer, a certain mathematical combination of
space and time, chosen so that changes in space cancel the changes in
time, is the same for everyone. Relativity's intimate linkage of space and
time in the invariant space-time interval gives rise to the notion that in
reality the world is four-dimensional—consisting of three spatial dimen-
sions and one time dimension. The space-time interval is a kind of "dis-
tance" in that four-dimensional space.

According to Einstein, only such absolute quantities can be used as the
ingredients of a valid physical law. Laws built to Einstein's specifications
are called "covariant." Today we know for sure that if a physical theory
does not have a covariant formulation it cannot represent the facts. By
looking at where it's not covariant—wherever it uses a relative concept
rather than an absolute one—we can even predict exactly how it must fail.

The luminiferous ether—a body that's "standing still in space"—is a
manifestly non-covariant concept because it is standing still for only one
observer. According to Einstein, the physics governing the interaction of
bodies A and B can depend only on their relative motion, not on their
velocity measured with respect to some special reference frame. If Ein-
stein's theory is correct—and it has been abundantly verified—the con-
cept of the ether can never enter into any correct physical law. The ether
is quite literally a useless concept: there is no use for it in physics. However
a light wave travels through space—light's manner of propagation is still a
bit of a mystery—it cannot go via a medium made of invisible Silly Putty
which fills up the universe.

Despite its central role in Victorian science, the luminiferous ether
plays no part whatsoever in modern physics. The ether is a reality that
failed. We consider next a reality that succeeded—the notion that matter
is made out of atoms.

The Atomicity of Matter

The idea that the world consists of standard little parts originated in
antiquity. It would be hard to find a more eloquent statement of the
atomic hypothesis than that of Democritus of Abdera, who wrote (about

500 B.C.): "By convention sour, by convention sweet, by convention
colored; in reality, nothing but Atoms and the Void."

The atomic hypothesis existed side by side with the belief that the
world consisted of transformations of a single continuous substance which
some called "Fire," others "Air" or "Water". The commonplace observa-
tion that water could take solid, liquid, or gaseous forms depending on
temperature was taken as an example of how one seamless substance
might be able to simulate the world's enormous variety. However, until
the nineteenth century the arguments for the continuum and the atomic
hypotheses were mainly rhetorical; little evidence existed for either of
these views.

In 1808 the British chemist John Dalton discovered that chemical sub-
stances combine according to fixed ratios—one part oxygen, for example,
combines with two parts hydrogen to make water, provided each of these
parts is assigned a standard weight. The standard weight of oxygen is
sixteen times the standard weight of hydrogen. Dalton proposed that
these constant combining ratios represented the combination of actual
atoms whose atomic weights were proportional to the standard weights.
According to Dalton, bulk hydrogen combines with bulk oxygen in a two-
to-one ratio because water, in reality, is composed of two hydrogen atoms
plus an oxygen atom. Dalton took these constant chemical ratios as tokens
of an invisible atomic reality.

Most scientists were convinced by Dalton's arguments and accepted
the real existence of atoms as an explanation of chemical reactions. How-
ever, a small but prestigious minority opposed the atomic hypothesis on
the grounds that it went beyond the facts.

In 1826 Dalton received the Royal Society of London's medal of honor
from famous British chemist Humphry Davy. While celebrating the im-
portance of Dalton's work, Davy cautioned that the word "atom" could
only realistically have the meaning "chemical equivalent"—that the atom
was a unit of chemical reaction rather than a material entity. Davy praised
Dalton for his discovery of the law of chemical proportions and predicted
that his fame would rest on this practical discovery rather than on his
speculations concerning invisible entities behind the phenomena.

Chemists of diverse nationalities united to oppose the atomic hypothe-
sis. For instance, the distinguished French chemist Jean Baptiste Dumas
proclaimed: "If I were master of the situation, I would efface the word
atom from Science, persuaded that it goes further than experience, and
that in chemistry, we should never go further than experience." The Ger-

man chemist Kekule, famous for his discovery of the benzene ring (which
he presumably interpreted purely symbolically) had this to say about at-
oms: "The question whether atoms exist or not has little significance from
a chemical point of view; its discussion belongs rather to metaphysics. In
chemistry we have only to decide whether the assumption of atoms is a
hypothesis adapted to the explanation of chemical phenomena."

"And who has ever seen a gas molecule or an atom?" chided Marcelin
Berthelot, expressing the disdain that many of his fellow chemists felt for
invisible entities inaccessible to experiment. Even its defenders saw little
hope of ever directly verifying the atomic hypothesis: the size of these
elementary entities—if they were really there at all—was estimated to be
thousands of times smaller than a wavelength of light, hence technically
forever invisible.

Wilhelm Ostwald, a German chemist who later received the Nobel
Prize, turned to the field of chemical thermodynamics for an alternative to
the atomic hypothesis. The two laws of thermodynamics—which require
conservation of energy and an entropy-based limit on this energy's utiliza-
tion—had been extended by Maxwell and Gibbs to describe successfully
the intimate details of physical and chemical reactions without recourse to
the atomic hypothesis. The success of the thermodynamic approach con-
vinced Ostwald and his followers that molecules and atoms were imagina-
tive fictions and that the real underlying component of the universe was
energy, in its various forms.

Because of their faith in energy rather than atoms as an explanatory
principle, Ostwald and his colleagues were called "energeticists." Debates
in the journals and at scientific conferences between the supporters of the
atomic hypothesis and the energeticists were sharp and emotional. The
bitter opposition of the anti-atomists to his work on the kinetic theory of
gases may have been partly responsible for the suicide of Ludwig Boltz-
mann, a brilliant but troubled theoretical physicist, in 1906.

In 1905, the same year he conceived the theory of relativity which
demolished the luminiferous ether, Einstein published a paper on Brown-
ian motion that pointed the way to conclusive experiments bearing on the
real existence of atoms.

Whenever micron-sized particles are suspended in a liquid they undergo
a perpetual quivering dance whose origin had been a mystery since its
discovery in 1828 by Scottish botanist Robert Brown. Early experiments
on Brownian motion were performed with pollen grains and the activity
was believed to be of biological origin. I remember my first glimpse of

what I took to be "cells" under a powerful microscope, and was fascinated
by their ceaseless pulsations like tiny heartbeats until my teacher told me
that I was looking at the Brownian motion of dirt particles. (Actually,
when I finally spotted the real cells they didn't seem so interesting as the
dancing dirt.) When it was discovered that any sort of finely divided
matter would show such agitation (even stone from the Sphinx was pulver-
ized and made to dance under the microscope), the biological hypothesis
was discarded and various physical mechanisms proposed: temperature
gradients, surface tension, obscure electrochemical effects. None of these
quite worked. Brownian motion remained a minor mystery tucked away in
an obscure corner of physics.

Einstein explained Brownian motion as the action of numerous atoms
in motion colliding with the Brownian particle. This explanation had been
previously rejected because the atoms were millions of times less massive
than the Brownian particle, and their collective pressure could lead to no
net motion because equal amounts of atoms were pushing in every direc-
tion.

Einstein showed that although the number of atoms striking the
Brownian particle from each direction is equal on the average, the fluctua-
tions away from this average lead to unbalanced forces in random direc-
tions. In any random process, the relative fluctuations from an average
value is inversely proportional to the square root of the number of samples
—the smaller the sample, the bigger the fluctuations. For a large particle,
the bulk pressure of the surrounding atoms is indeed evenly balanced, but
for a small particle, the fluctuations in the number of impinging atoms is
sufficient to propel it in an unpredictable direction with a predictable
force. Einstein showed how this random force would vary with tempera-
r::e and particle size. If atoms existed, Einstein's model of Brownian
motion would allow you actually to count the number of atoms striking a
Brownian particle by measuring how far it drifts in response to these
fluctuation forces.

In a series of ingenious experiments the French physicist Jean Baptiste
Perrin verified Einstein's model and succeeded for the first time in actu-
ally counting the number of atoms in a drop of water. Perrin published his
direct verification of the atomic hypothesis in 1913, in a book called
simply Les Atomes.

In 1895 Ostwald railed against the atomic hypothesis in a speech enti-
tled "On Overcoming Scientific Materialism": "We must renounce the
hope of representing the physical world by referring natural phenomena to

a mechanics of atoms. 'But'—I hear you say—'but what will we have left
to give us a picture of reality if we abandon atoms?' To this I reply: "Thou
shalt not take unto thee any graven image, or any likeness of anything.'
Our task is not to see the world through a dark and distorted mirror, but
directly, so far as the nature of our minds permits. The task of science is to
discern relations among realities, i.e., demonstrable and measurable quan-
tities ... It is not a search for forces we cannot measure, acting between
atoms we cannot observe."

But in response to the work of Einstein and Perrin, the leader of the
energeticists bowed to the experimental evidence and finally accepted the
real existence of atoms: "I am now convinced," said Ostwald, "that we
have recently become possessed of experimental evidence of the discrete
or grained nature of matter, which the atomic hypothesis sought in vain
for hundreds and thousands of years. [Experiments such as Perrin's] justify
the most cautious scientist in now speaking of the experimental proof of
the atomic nature of matter. The atomic hypothesis is thus raised to the
position of a scientifically well-founded theory."

More recently (1957) philosopher of science Hans Reichenbach
summed up the modern opinion concerning the atomic hypothesis: "The
atomic character of matter belongs to the most certain facts of our present
knowledge ... we can speak of the existence of atoms with the same
certainty as the existence of stars." The actuality of atoms is a reality that
succeeded. Nobody today doubts that atoms really exist.

According to the pragmatists, science is like a cookbook—mere recipes
for ordering phenomena. Once you have a recipe that works, what more
could you ask for? Realists want more. They believe that a good theory
should act as a guidebook to what's really out there in the world. In the
words of Michael Polanyi, a distinguished scientific realist: "A theory
which we acclaim as rational in itself is accredited with prophetic powers.
We accept it in the hope of making contact with reality; so that being
really true, our theory may yet show forth its truth through future centu-
ries in ways undreamed of by its authors."

Quantum theory has been universally successful in describing phenom-
ena at all levels accessible to experiment. It's a perfect cookbook, for
whatever we choose to cook up. However, this comprehensive practical
success has been accompanied by an unprecedented disagreement as to
what quantum theory actually means, and a corresponding confusion as to

what sort of reality supports the phenomenal world. In the next chapter I
examine some of the contradictory quantum realities which different phys-
icists claim to be the "real reality" that lies behind the external appear-
ances of this world we live in.

2 - Physicists
Losing Their Grip

"No development of modern science has had a more profound im-
pact on human thinking than the advent of quantum theory.
Wrenched out of centuries-old thought patterns, physicists of a
generation ago found themselves compelled to embrace a new
metaphysics. The distress which this reorientation caused contin-
ues to the present day. Basically physicists have suffered a severe
loss: their hold on reality."

---Bryce DeWitt
---Neill Graham

One of the best-kept secrets of science is that physicists have lost their
grip on reality.

News of the reality crisis hardly exists outside the physics community.
What shuts out the public is partly a language barrier—the mathematical
formalism that facilitates communication between scientists is incompre-
hensible to outsiders—and partly the human tendency of physicists to
publicize their successes while soft-pedalling their confusions and uncer-

tainties. Even among themselves, physicists prefer to pass over the uncom-
fortable reality issue in favor of questions "more concrete". Recent popu-
larizations such as Heinz Pagels' Cosmic Code have begun to inform the
public about the reality crisis in physics. In Quantum Reality I intend to
examine how physicists deal with reality—or fail to deal with it—in clear
and unprecedented detail.

Nothing exposes the perplexity at the heart of physics more starkly than
certain preposterous-sounding claims a few outspoken physicists are mak-
ing concerning how the world really works. If we take these claims at face
value, the stories physicists tell resemble the tales of mystics and madmen.
Physicists are quick to reject such unsavory associations and insist that
they speak sober fact. We do not make these claims out of ignorance, they
say, like ancient mapmakers filling in terra incognitas with plausible geog-
raphy. Not ignorance, but the emergence of unexpected knowledge forces
on us all new visions of the way things really are.

The new physics vision is still clouded, as evidenced by the multiplicity
of its claims, but whatever the outcome it is sure to be far from ordinary.
To give you a taste of quantum reality, I summarize here the views of its
foremost creators in the form of eight realities which represent eight ma-
jor guesses as to what's really going on behind the scenes. Later we will
look at each of these realities in more detail and see how different physi-
cists use the same data to justify so many different pictures of the world.

Quantum Reality #1: The Copenhagen interpretation, Part I (There
is no deep reality.) No one has influenced more our notions of what the
quantum world is really about than Danish physicist Niels Bohr, and it is
Bohr who puts forth one of quantum physics' most outrageous claims: that
there is no deep reality. Bohr does not deny the evidence of his senses.
The world we see around us is real enough, he affirms, but it floats on a
world that is not as real. Everyday phenomena are themselves built not out
of phenomena but out of an utterly different kind of being.

Far from being a crank or minority position, "There is no deep reality"
represents the prevailing doctrine of establishment physics. Because this
quantum reality was developed at Niels Bohr's Copenhagen institute, it is
called the "Copenhagen interpretation." Undaunted by occasional chal-
lenges by mavericks of realist persuasion, the majority of physicists swear
at least nominal allegiance to Bohr's anti-realist creed. What more glaring
indication of the depth of the reality crisis than the official rejection of
reality itself by the bulk of the physics community?

Einstein and other prominent physicists felt that Bohr went too far in
his call for ruthless renunciation of deep reality. Surely all Bohr meant to
say was that we must all be good pragmatists and not extend our specula-
tions beyond the range of our experiments. From the results of experi-
ments carried out in the twenties, how could Bohr conclude that no future
technology would ever reveal a deeper truth? Certainly Bohr never in-
tended actually to deny deep reality but merely counseled a cautious skep-
ticism toward speculative hidden realities.

Bohr refused to accept such a watered-down version of the Copenhagen
doctrine. In words that must chill every realist's heart, Bohr insisted:
"There is no quantum world. There is only an abstract quantum descrip-
tion."

Werner Heisenberg, the Christopher Columbus of quantum theory,
first to set foot on the new mathematical world, took an equally tough
stand against reality-nostalgic physicists such as Einstein when he wrote:
"The hope that new experiments will lead us back to objective events in
time and space is about as well founded as the hope of discovering the end
of the world in the unexplored regions of the Antarctic."

The writings of Bohr and Heisenberg have been criticized as obscure
and open to many interpretations. Recently Cornell physicist N. David
Mermin neatly summed up Bohr's anti-realist position in words that leave
little room for misunderstanding: "We now know that the moon is de-
monstrably not there when nobody looks." (We will take a look at
Mermin's "demonstration" in Chapter 13.)

Quantum Reality #2: The Copenhagen interpretation, Part II (Real-
ity is created by observation.) Although the numerous physicists of the
Copenhagen school do not believe in deep reality, they do assert the
existence of phenomenal reality. What we see is undoubtedly real, they
say, but these phenomena are not really there in the absence of an obser-
vation. The Copenhagen interpretation properly consists of two distinct
parts: 1. There is no reality in the absence of observation; 2. Observation
creates reality. "You create your own reality," is the theme of Fred Wolf's
Taking the Quantum Leap.

Which of the world's myriad processes qualify as observations? What
special feature of an observation endows it with the power to create real-
ity? Questions like these split the observer-created reality school into sev-
eral camps, but all generally subscribe to quantum theorist John Wheeler's
memorable maxim for separating what is real in the world from what is

not. "No elementary phenomenon is a real phenomenon until it is an
observed phenomenon," Wheeler proclaims. Without a doubt, Mermin's
description of the inconstant moon qualifies him for membership in the
observer-created reality school.

The belief that reality is observer-created is commonplace in philoso-
phy, where it serves as the theme for various forms of idealism. Bertrand
Russell recalls his fascination with idealism during his student days at
Trinity College: "In this philosophy I found comfort for a time . . .
There was a curious pleasure in making oneself believe that time and
space are unreal, that matter is an illusion and that the world really con-
sists of nothing but mind."

Since pondering matter is their bread and butter, not many physicists
would share Russell's enjoyment of matter as mere mirage. However, like
it or not, through their conscientious practice of quantum theory more
than a few physicists have strayed within hailing distance of the idealist's
dreamworld.

Quantum Reality #3 (Reality is an undivided wholeness.) The views
of Walter Heitler, author of a standard textbook on the light/matter inter-
action, exemplify a third unusual claim of quantum physicists: that in spite
of its obvious partitions and boundaries, the world in actuality is a seamless
and inseparable whole—a conclusion which Fritjof Capra develops in Tao
of Physics and connects with the teachings of certain oriental mystics.
Heitler accepts an observer-created reality but adds that the act of obser-
vation also dissolves the boundary between observer and observed: "The
observer appears, as a necessary part of the whole structure, and in his full
capacity as a conscious being. The separation of the world into an 'objec-
tive outside reality' and 'us,' the self-conscious onlookers, can no longer be
maintained. Object and subject have become inseparable from each
other."

Physicist David Bohm of London's Birkbeck College has especially
stressed the necessary wholeness of the quantum world: "One is led to a
new notion of unbroken wholeness which denies the classical analyzability
of the world into separately and independently existing parts . . . The
inseparable quantum interconnectedness of the whole universe is the fun-
damental reality."

Quantum wholeness is no mere replay of the old saw that everything is
connected to everything else, no twentieth-century echo, for instance, of
Newton's insight that gravity links each particle to every other. All ordi-

nary connections—gravity, for one—inevitably fall off with distance, thus
conferring overwhelming importance on nearby connections while distant
connections become irrelevant. Undoubtedly we are all connected in un-
remarkable ways, but close connections carry the most weight. Quantum
wholeness, on the other hand, is a fundamentally new kind of together-
ness, undiminished by spatial and temporal separation. No casual hookup,
this new quantum thing, but a true mingling of distant beings that reaches
across the galaxy as forcefully as it reaches across the garden.

Quantum Reality #4: The many-worlds interpretation (Reality con-
sists of a steadily increasing number of parallel universes.) Of all claims of
the New Physics none is more outrageous than the contention that myri-
ads of universes are created upon the occasion of each measurement act.
For any situation in which several different outcomes are possible (flipping
a coin, for instance), some physicists believe that all outcomes actually
occur. In order to accommodate different outcomes without contradiction,
entire new universes spring into being, identical in every detail except for
the single outcome that gave them birth. In the case of a flipped coin, one
universe contains a coin that came up heads; another, a coin showing tails.
Paul Davies champions this claim, known as the many-worlds interpreta-
tion, in his book Other Worlds. Science fiction writers commonly invent
parallel universes for the sake of a story. Now quantum theory gives us
good reason to take such stories seriously.

Writing in Physics Today, a major magazine of the American physics
community, Bryce DeWitt describes his initial contact with the many-
worlds interpretation of quantum theory:

"I still recall vividly the shock I experienced on first encountering this
multiworld concept. The idea of 10100+[to the power of 100+] slightly imperfect copies of one-
self all constantly splitting into further copies, which ultimately become
unrecognizable, is not easy to reconcile with common sense . . ."

Invented in 1957 by Hugh Everett, a Princeton graduate student, the
many-worlds interpretation is a latecomer to the New Physics scene. De-
spite its bizarre conclusion, that innumerable parallel universes each as
real as our own actually exist, Everett's many-worlds picture has gained
considerable support among quantum theorists. Everett's proposal is par-
ticularly attractive to theorists because it resolves, as we shall see, the
major unsolved puzzle in quantum theory—the notorious quantum mea-
surement problem.

These four quantum realities should give you some feeling for the diversity
of claims regarding the world's ultimate nature. While followers of Ever-
ett bear witness to uncountable numbers of quantum worlds, plus more on
the way, students of Bohr and Heisenberg insist that there is not even one
quantum world. In their struggle to gain firm footing amidst the slippery
bricks of quantum fact, physicists have invented more realities than four.
Keep your wits about you as we press on.

Quantum Reality #5: Quantum logic (The world obeys a non-human
kind of reasoning.). Quantum logicians argue that the quantum revolution
goes so deep that replacing new concepts with old will not suffice. To cope
with the quantum facts we must scrap our very mode of reasoning, in
favor of a new quantum logic.

Logic is the skeleton of our body of knowledge. Logic spells out how we
use some of the shortest words in the language, words such as and, or, and
not. The behavior of these little linguistic connectors governs the way we
talk about things, and structures, in turn, the way we think about them.

For two thousand years, talk about logic (in the West) was cast in the
syllogistic mold devised by Aristotle. In the mid-nineteenth century,
George Boole, an Irish schoolteacher, reduced logical statements to simple
arithmetic by inventing an artificial symbolic language which laid bare the
logical bones of ordinary language.

Boole's clear codification of the rules of reason jolted logic out of the
Middle Ages and launched the now-flourishing science of mathematical
logic. Outside the mathematical mainstream, a few creative logicians
amused themselves by constructing "crazy logics" using rules other than
Boole's. These deviant designs for and/or/not, although mathematically
consistent, were considered mere curiosities since they seemed to fit no
human pattern of discourse.

However, according to some New Physicists, one of these crazy logics
may be just what we need to make sense out of quantum events. Listen to
quantum theorist David Finkelstein calling for mutiny against the rules of
Boole:

"Einstein threw out the classical concept of time; Bohr throws out the
classical concept of truth . . . Our classical ideas of logic are simply
wrong in a basic practical way. The next step is to learn to think in the
right way, to learn to think quantum-logically."

As an example of the usefulness of changing your mind rather than chang-
ing your physics, quantum logicians point to Einstein's general theory of
relativity, which achieved in the realm of geometry what they propose to
do with logic.

Geometry is the science of points and lines. For two thousand years
only one geometry existed, its rules compiled by the Greek mathematician
Euclid in his bestselling book The Elements, which once rivaled the Bible
in popularity. The latest revival of Euclid's Elements is your high school
geometry book.

Coincident with Boole's pioneer work in logic, a few adventurous math-
ematicians thought up "crazy geometries," games points and lines could
play outside of Euclid's rules. Chief architect of the New Geometry was
the Russian Nicolai Lobachevski along with German mathematicians Karl
Gauss and Georg Riemann. Their cockeyed geometries were regarded, like
non-Boolean logics, as high mathematical play, clever business but out of
touch with reality. Euclidean geometry, as everyone knows, was the geom-
etry, being after all, nothing but common sense applied to triangles and
other geometric figures.

However, in 1916 Einstein proposed a radical new theory of gravity that
demolished the Euclidean monopoly. Einstein, in opposition to Newton
and everybody else, declared that gravity is not a force but a curvature in
space-time. Objects in free fall are truly free and move in lines as straight
as can be—that is, lines straight by the standards of a gravity-warped
geometry. Einstein's theory has testable consequences: for instance the
deflection of starlight grazing the sun (confirmed by Eddington in 1919)
and the existence of black holes (according to astrophysicists, in the con-
stellation Cygnus, black hole Cygnus X-l resides). On Earth, where our
common sense was formed, gravity is weak and space almost Euclidean;
out near X-l, high school geometry flunks.

Einstein's lesson is plain to see, say the quantum logicians. The question
of the world's true geometry is not settled by common sense but by experi-
ment. Likewise with logic. For the rules of right reason, look not inside
your own head but get thee to a laboratory.

Quantum Reality #6: Neorealism (The world is made of ordinary
objects.) An ordinary object is an entity which possesses attributes of its
own whether observed or not. With certain exceptions (mirages, illusions,
hallucinations), the world outside seems populated with objectlike entities.
The clarity and ubiquity of ordinary reality has seduced a few physicists—I
call them neorealists—into imagining that this familiar kind of reality can
be extended into the atomic realm and beyond. However, the unremark-
able and common-sense view that ordinary objects are themselves made of
objects is actually the blackest heresy of establishment physics.

"Atoms are not things," says Heisenberg, one of the high priests of the
orthodox quantum faith, who likened neorealists to believers in a flat
earth. "There is no quantum world," warned Bohr, the pope in Copenha-
gen; "there is only an abstract quantum description."

Neorealists, on the other hand, accuse the orthodox majority of wal-
lowing in empty formalism and obscuring the world's simplicity with
needless mystification. Instead they preach return to a pure and more
primitive faith. Chief among neorealist rebels was Einstein, whose passion
for realism pitted him squarely against the quantum orthodoxy: "The
Heisenberg-Bohr tranquilizing philosophy—or religion?—is so delicately
contrived that, for the time being, it provides a gentle pillow for the true
believer from which he cannot very easily be aroused. So let him lie
there."

Despite their Neanderthal notions, no one could accuse neorealists of

ignorance concerning the principles of quantum theory. Many of them
were its founding fathers. Besides Einstein, prominent neorealists include
Max Planck, whose discovery of the constant of action sparked the quan-
tum revolution; Erwin Schrodinger, who devised the wave equation every
quantum system must obey; and Prince Louis de Broglie, who took quan-
tum theory seriously enough to predict the wave nature of matter.

De Broglie, a French aristocrat whose wartime involvement in radio
swerved his research from church history into physics, fought for ordinary
realism until 1928 when he converted to the statistical interpretation (an-
other name for Copenhagenism). Twenty years later, however, influenced
by David Bohm's neorealist revival, de Broglie recanted and returned to
the faith of his youth:

"Those interested in the psychology of scientists may be curious about
the reasons for my unexpected return to discarded ideas ... I am think-
ing not so much of my constant difficulties in developing a statistical
interpretation of wave mechanics, or even of my secret hankering after
Cartesian clarity in the midst of the fog which seemed to envelop quan-
tum physics [but the fact that, as I examined the statistical picture] I
could not help being struck by the force of the objections to it and by a
certain obscurity in the arguments in its defense ... too abstract . . .
too schematic ... I realized that I had been seduced by the current
fashion, and began to understand why I had been so uneasy whenever I
tried to give a lucid account of the probability interpretation."

One of the physics community's few traditions is the custom of celebrat-
ing the birthdays of its great men with a Festschrift—a festival of papers.
In 1982, Louis de Broglie, ninety years old and gloriously unrepentant, was
honored in this scholarly manner by his scientific colleagues. Virtually
every neorealist in the world attended de Broglie's birthday party: there

no need to send out for extra chairs.

Einstein, despite his numerous contributions to its success, never ac-
cepted quantum theory into his heart and stubbornly held to the old-
fashioned belief that a realistic vision of the world was compatible with
the quantum facts. During the thirties Einstein and Bohr engaged in an
extended debate on the quantum reality question. Bohr argued that as far
as reality was concerned, quantum theory was a closed book. By 1928
perceptive physicists had already grasped the theory's essence. Quantum
theory would develop in detail but its principles would not change. Bohr's

confidence has been upheld so far; fifty years later, physicists still follow
the old rules.

Quantum theory is complete as it stands, said Bohr. It has no need of
ordinary objects. Furthermore such objects cannot be added without spoil-
ing its predictive success. Ordinary objects are not merely unnecessary
luxuries in quantum theory, they are strictly impossible.

Einstein's strategy was to confront Bohr with a series of thought experi-
ments which aimed to show that quantum theory had left something out.
He did not attempt to show that the theory was wrong, but by demon-
strating that it was incomplete Einstein hoped to open the door for what
he called "elements of reality."

As the winners tell the story, Bohr closed each of Einstein's loopholes,
but in the minds of each the debate was never settled. Long after their
arguments had ended, on the day Bohr died, his blackboard contained a
drawing of one of Einstein's thought experiments. Bohr struggled with
Einstein to the end.

Einstein too never gave up. In his autobiography he expresses his final
thoughts on the quantum reality question: "I still believe in the possibility
of a model of reality—that is, of a theory which represents things them-
selves and not merely the probability of their occurrence."

Quantum Reality #7 (Consciousness creates reality.) Among observer-
created realists, a small faction asserts that only an apparatus endowed
with consciousness (even as you and I) is privileged to create reality. The
one observer that counts is a conscious observer. Denis Postle examines
reality-creating consciousness in Fabric of the Universe. I include this
quantum reality not only because it is so outlandish but because its sup-
porters are so illustrious. Consciousness-created reality adherents include
light/matter physicist Walter Heitler, already cited in connection with
undivided wholeness, Fritz London, famous for his work on quantum liq-
uids, Berkeley S-matrix theorist Henry Pierce Stapp, Nobel laureate Eu-
gene Wigner, and world-class mathematician John von Neumann.

Hungarian-born von Neumann was the mathematical midwife for some
of the twentieth century's most exciting developments. Wherever things
were hottest, the brilliant von Neumann seemed to be there lending a
hand. In the late forties he invented the concept of the stored-program
computer; today's computer scientists refer to all computers from pocket
calculators to giant IBMs as "von Neumann machines." In collaboration
with Oskar Morgenstern, von Neumann laid the mathematical foundation

for strategic game theory, on which much government and corporate pol-
icy in both the East and the West is based. He also worked on early robots
and helped develop the atom bomb. In 1936 with Harvard mathematician
Garrett Birkhoff he came up with the idea of quantum logic, but von
Neumann's biggest contribution to quantum reality research was his book
on quantum theory.

By the late twenties physicists had constructed a quantum theory that
met their daily needs: they possessed a rough mathematical structure
which organized the quantum facts. At that point von Neumann entered
the picture, putting physicists' crude theory into rigorous form, settling
quantum theory into an elegant mathematical home called "Hilbert
space" where it resides to this day, and awarding the mathematician's seal
of approval to physicists' fledgling theory.

In 1932 von Neumann set down his definitive vision of quantum theory
in a formidable tome entitled Die Mathematische Grundlagen der
Quantenmechanik. Our most general picture of quantum theory is essen-
tially the same as that outlined by von Neumann in Die Grundlagen (The
Foundations). Von Neumann's book is our quantum bible. Like many
other sacred texts, it is read by few, venerated by many. Despite its impor-
tance it was not translated into English until 1955.

Many of the issues I discuss in Quantum Reality were first made public
in von Neumann's book. For instance, there is von Neumann '$ proof that
if quantum theory is correct, the world cannot be made of ordinary objects
—i.e., the neorealist interpretation is logically impossible. Von Neumann
posed, but did not solve to everyone's satisfaction, the famous quantum
measurement problem which is the central issue of the quantum reality
question. In addition, von Neumann was the first to show how quantum
theory suggests an active role for the observer's consciousness. Physical
objects would have no attributes, von Neumann said, if a conscious ob-
server were not watching them.

Von Neumann himself merely hinted at consciousness-created reality in
dark parables. His followers boldly took his arguments to their logical
conclusion: if we accept von Neumann's version of quantum theory, they
say. a consciousness-created reality is the inevitable outcome.

At the logical core of our most materialistic science we meet not dead
matter but our own lively selves. Eugene Wigner, von Neumann's Prince-
ton colleague and fellow Hungarian (they went to the same high school in
Budapest), comments on this ironic turn of events: "It is not possible to
formulate the laws of quantum mechanics in a fully consistent way with-

out reference to the consciousness ... It will remain remarkable in
whatever way our future concepts may develop, that the very study of the
external world led to the conclusion that the content of the consciousness
is an ultimate reality."

Quantum Reality #8: The duplex world of Werner Heisenberg (The
world is twofold, consisting of potentials and actualities.) Most physicists
believe in the Copenhagen interpretation, which states that there is no
deep reality (QR #1) and observation creates reality (QR #2). What
these two realities have in common is the assertion that only phenomena
are real; the world beneath phenomena is not.

One question which this position immediately brings to mind is this:
"If observation creates reality, what does it create this reality out of? Are
phenomena created out of sheer nothingness or out of some more substan-
tial stuff?" Since the nature of unmeasured reality is unobservable by
definition, many physicists dismiss such questions as meaningless on prag-
matic grounds.

However, since it describes measured reality with perfect exactness,
quantum theory must contain some clues concerning the raw material out
of which phenomena spring. Perhaps using the power of imagination we
can peer beneath this theory and make some shrewd guess about the
background world against which our familiar world of solid observations
stands.

Werner Heisenberg was fully aware of the difficulties of attempting to
describe the subphenomenal world: "The problems of language here are
really serious," he said. "We wish to speak in some way about the structure
of the atoms and not only about the 'facts'—for instance, the water drop-
lets in a cloud chamber. But we cannot speak about the atoms in ordinary
language." Although he realized the difficulty in doing so, Heisenberg was
one of the few physicists to try to express what he saw when he looked
into quantum reality.

According to Heisenberg, there is no deep reality—nothing down there
that's real in the same sense as the phenomenal facts are real. The unmea-
sured world is merely semireal, and achieves full reality status during the
act of observation: "In the experiments about atomic events we have to do
with things and facts, with phenomena that are just as real as any phe-
nomena in daily life. But the atoms and the elementary particles them-
selves are not as real; they form a world of potentialities or possibilities
rather than one of things or facts . . .

"The probability wave . . . means a tendency for something. It's a
quantitative version of the old concept of potentia in Aristotle's philoso-
phy. It introduces something standing in the middle between the idea of
an event and the actual event, a strange kind of physical reality just in the
middle between possibility and reality."

Heisenberg's world of potentia is both less real and more real than our
own. It is less real because its inhabitants enjoy a ghostly quantum lifestyle
consisting of mere tendencies, not actualities. On the other hand, the
unmeasured world is more real because it contains a wealth of coexistent
possibilities, most of which are contradictory. In Heisenberg's world a
flipped coin can show heads and tails at the same time, an eventuality
impossible in the actual world.

One of the inevitable facts of life is that all of our choices are real
choices. Taking one path means forsaking all others. Ordinary human
experience does not encompass simultaneous contradictory events or mul-
tiple histories. For us, the world possesses a singularity and concreteness
apparently absent in the atomic realm. Only one event at a time happens
here; but that event really happens.

The quantum world, on the other hand, is not a world of actual events
like our own but a world full of numerous unrealized tendencies for action.
These tendencies are continually on the move, growing, merging, and
dying according to exact laws of motion discovered by Schrodinger and his
colleagues. But despite all this activity nothing ever actually happens there.
Everything remains strictly in the realm of possibility.

Heisenberg's two worlds are bridged by a special interaction which
physicists call a "measurement." During the magic measurement act, one
quantum possibility is singled out, abandons its shadowy sisters, and sur-
faces in our ordinary world as an actual event. Everything that happens in
our world arises out of possibilities prepared for in that other—the world
of quantum potentia. In turn, our world sets limits on how far crowds of
potentia can roam. Because certain facts are actual, not everything is
possible in the quantum world. There is no deep reality, no deep reality-as-
we-know-it. Instead the unobserved universe consists of possibilities, ten-
dencies, urges. The foundation of our everyday world, according to Hei-
senberg, is no more substantial than a promise.

Physicists do not put forth these quantum realities as science fiction
peculations concerning worlds that might have been, but as serious pic-
es of the one world we actually live in: the universe outside your door.

Since these quantum realities differ so radically, one might expect them to
have radically different experimental consequences. An astonishing feature
of these eight quantum realities, however, is that they are experimentally
indistinguishable. For all presently conceivable experiments, each of these
realities predicts exactly the same observable phenomena.

The ancient philosophers faced a similar reality crisis. For instance
three ancient realities—1. The world rests on a turtle's back; 2. The world
is bottomlessly solid; 3. The world floats in an infinite ocean—led to
identical consequences as far as anyone could tell at that time.

Likewise modern physicists do not know how to determine experimen-
tally what kind of world they actually live in. However, since "reality has
consequences" we might hope that future experiments, not bound by our
current concepts of measurability, will conclusively establish one or more
of these bizarre pictures as top-dog reality. At present, however, each of
these quantum realities must be regarded as a viable candidate for "the
way the world really is." They may, however, all be wrong.

Physicists' reality crisis is twofold: 1. There are too many of these quan-
tum realities; 2. All of them without exception are preposterous. Some of
these quantum realities are compatible with one another. For instance QR
# 1 (There is no deep reality) and QR # 2 (Reality is observer-created) are
in fact two halves of a single consistent picture of the world called the
Copenhagen interpretation. But other quantum realities are contradictory:
in the many-worlds interpretation (QR #4), for instance, the world's
deep reality consists of quadrillions of simultaneous universes, each one as
real as our own, which maximally mocks Bohr's no-deep-reality claim. Not
only can physicists not agree on a single picture of what's really going on
in the quantum world, they are not even sure that the correct picture is on
this list.

None of the conflicting options which physicists have proposed as possible
pictures of our home universe can be considered ordinary. Even that quan-
tum reality closest to old-fashioned notions of how a world should behave
—the neorealist contention (QR # 6) that the world is made out of ordi-
nary objects—contains, as we shall see, the requirement that some of these
objects move faster than light, a feature that entails unusual consequences:
time travel and reversed causality, for example.

This book is a snapshot of the reality crisis in physics taken at a moment
when that crisis is not yet resolved. Nobody knows how the world will
seem one hundred years from now. It will probably appear very different
from what we now imagine. Here's what John Wheeler, a physicist ac-

tively concerned with the nature of quantum reality, imagines when he
looks into the future:

"There may be no such thing as the 'glittering central mechanism of
the universe' to be seen behind a glass wall at the end of the trail. Not
machinery but magic may be the better description of the treasure that is
waiting."

3 - Quantum Theory
Takes Charge

"Some physicists would prefer to come back to the idea of an objec-
tive real world whose smallest parts exist objectively in the same
sense as stones or trees exist independently of whether we observe
them. This however is impossible."

---Werner Heisenberg

At the end of the nineteenth century, physicists possessed a comprehen-
sive picture of the way the world worked. A few great men had solved the
big problems. The task of their successors was to fill in the details, to
measure the next decimal place. No glory there. By explaining everything,
classical physics seemed to have put itself out of business. "Physics is
finished, young man. It's a dead-end street," said Max Planck's teacher.
He advised Planck to be a concert pianist instead.

The triumph of classical physics was short-lived: the paradoxes of quan-
tum theory soon swept away its Victorian certainties. But while it lasted,
nineteenth-century physics stood as a high-water mark of applied common

sense. Not only did it appear to explain all the facts, but it did so in ways
that were clear and picturable.

Matter and Field—The Stuff of Classical Physics

Classical physicists were able to account for all the world's variety by
means of only two physical entities—matter and fields. In those innocent
days it went without saying that these entities were really there. Physicists'
reality crisis was yet to come.

Real matter. Real fields. Drop an apple from a bridge. The apple is
made of matter. It moves because the Earth's gravitational field pulls it.
Everything in the world works the same way: matter produces force fields,
which move other matter.

Classical physics recognized just two fields—electromagnetic and gravi-
tational—leaving open the possibility that more might be discovered.
Modern physics added only two fields to the classical duo—the strong
field, which holds the atomic nucleus together, and the weak field, which
breaks the nucleus apart in certain kinds of radioactive decay. Present
wisdom holds that these are all the fields nature needs to produce our kind
of universe, and that they are all likely one, united like electricity and
magnetism.

A classical field is a distribution of forces in space. The range of a field is
how far its force extends. The three classical forces fall off as the distance
squared, but they never go to zero: the range of these classical forces is
infinite. No matter how far from Earth you travel, its gravity still pulls on
you a little. On the other hand, the force of the two modern fields is
confined to the atomic nucleus. Because of their short ranges, the weak
and strong force fields were discovered last.

To describe how the classical world works we need two kind of laws:
laws of motion and field laws. Laws of motion tell matter how to move in a
particular force field. Field laws describe how each field depends on its
material source and how it spreads itself through space.

In the seventeenth century Isaac Newton discovered matter's laws of
motion. Force fields push matter along paths exactly prescribed by New-
ton's laws. These laws are deterministic: a given situation always leads to a
unique outcome. Locked to its tracks, the world cannot help but follow a
single path. Second by second the universe, like a giant clockwork, ticks
out Newton's inexorable laws, its future as fixed and immutable as its past.

In addition to his laws of motion, Newton discovered physics' first field
law—the inverse square behavior of the gravity field. To complete the
classical picture, only the field laws of electricity and of magnetism were
lacking. During the U.S. Civil War, Scottish physicist James Clerk Max-
well closed this gap, laying down the laws that govern electric and mag-
netic fields. Maxwell's laws were full of surprises. For instance, electricity
and magnetism turned out to be not two separate fields but different
aspects of a single electromagnetic field. Maxwell's field laws also unex-
pectedly solved one of physics' long-standing mysteries: the intrinsic na-
ture of light.

Fields whose range extends to the distant stars are attached to each
piece of matter. Shake that matter and you shake its field. Motion in a
field, like motion in a water bed, doesn't stand still but wiggles away as fast
as it can. Shaking a field makes waves—waves that travel at a certain
velocity.

Maxwell's laws tell us how to calculate the speed of waves in the electro-
magnetic field. How fast these waves move depends entirely on two elec-
tromagnetic facts: the force between two magnets and the force between
two electric charges. From the measured magnitudes of magnetic and
electric attraction, Maxwell figured how fast a wave of electromagnetism
must travel. His calculated speed was identical to the measured speed of
light. Maxwell conjectured that light was actually an electromagnetic wave
of extremely high frequency. Prior to Maxwell, who would have guessed
that this tenuous radiance that fills our eyes is akin to stolid storage batter-
ies and industrial magnets?

Furthermore, Maxwell surmised that there must exist invisible electro-
magnetic waves both lower and higher than light in the electromagnetic
spectrum. Heinrich Hertz's subsequent production of radio waves ("low-
frequency light") and the discovery of X rays ("high-frequency light") by
Roentgen verified Maxwell's bold conjecture: Light is a wave motion in
the electromagnetic field. Maxwell's discovery that the colors which de-
light the eye, the needle that guides the sailor, the lodestone, lightning,
the electric twitch in muscle and brain, are all manifestations of a single
physical field was classical physics' finest hour.

Ripples presumably exist in the gravity field, but gravity waves are too
weak to influence even the most delicate gravity meter. One of modern
physics' frontiers is the development of instruments sensitive enough to
respond to waves of gravity.

Classical physics in a nutshell: The universe consists of nothing but

matter and fields—and we know the laws of both. What more could a
physicist wish for? Well, it seems the picture was not quite perfect. If you
pressed them, classical physicists would confess a few tiny blemishes which
they were sure could be erased with a little extra effort. There was, for
instance, the black-body radiation puzzle.

Why Do Hot Objects Glow Red?

Colored objects have an intrinsic color; black objects don't. Heat up a
black object, however, and it begins to glow. Steelmakers for generations
gauged furnace temperatures by this black-body glow. They know, for
instance, that iron turns cherry-red around thirteen hundred degrees. For
physicists the black-body puzzle is how to calculate the color of that glow
at different temperatures.

A black object is made of little pieces of matter. Whenever these pieces
move, they shake waves into their attached electromagnetic fields—waves
our eyes interpret as colored light. The faster the particles move, the
higher the frequency of the light that is shaken off. As an object gets
hotter, its parts move faster. That's the sort of thinking that goes on in a
classical physicist's head as he sets out to calculate the color of black-body
glow.

Classical physicists had little idea of the nature of the light-emitting
particles in a block of hot iron but they assumed that, like everything else
in the world, they obeyed Newton's laws. Today we know that light is
caused by moving electrons. However, not only do electrons not follow
classical laws, they do not even follow a classical kind of law—that is, a law
that governs the motion of real objects.

For a quarter century after Maxwell announced the light-matter con-
nection, physicists attacked the black-body puzzle and kept coming up
with the same answer: black bodies should glow bright blue at all tempera-
tures.

In 1900, as the new century began, Max Planck, who against his teach-
er's advice had earned a degree in physics, not music, took up this black-
body puzzle. As a simplifying assumption he decided not to let the matter
particles vibrate any way they pleased; instead he artificially constrained
them to frequencies that follow this simple rule:

E = nhf

where E is the particle's energy, n is any integer, f is the frequency of the
particle's vibration, and h is a constant to be chosen by Planck. Planck's
rule restricts the particles to energies that are certain multiples of their
vibration frequency, as though energy only came in "coins" of denomina-
tion hf. Planck's constant h would later be called the "quantum of action"
because it has the dimensions of energy times time, a quantity known as
"action" in classical physics.

Planck's assumption was not justified by any physical reasoning but was
merely a trick to make the math easier to handle. Later in his calculations
Planck planned to remove this restriction by letting the constant h go to
zero. This would make the value of the "energy coin" so small that the
particle could once again have effectively any energy it pleased.

Planck discovered that he got the same blue glow as everybody else
when h went to zero. However, much to his surprise, if he set h to one
particular value, his calculation matched the experiment exactly (and vin-
dicated the experience of ironworkers everywhere). Hot iron glows red,
Planck showed, only if those particles exist whose energy is built from
"coins" of a particular denomination. Physicists politely ignored Planck's
work because although it gave the right answer, it did not play fair. This
funny restriction on energy was totally alien to classical physics. Newton's
laws permitted particles to have any energy they pleased.

Einstein's Three Papers

In the year 1905 Albert Einstein, a German Jew working in Switzerland as
an obscure patent clerk, published three papers in the German journal
Annalen der Physik that exploded onto the physics scene. Each of these
papers was a bombshell that shook the foundations of physics. Each by
itself would have sufficed to establish Einstein as a physicist of highest
rank. Three at once suggests divine inspiration.

Einstein's first paper explained the photoelectric effect—light's ability
to knock electrons out of metal—using Max Planck's new quantum of
action. Einstein's analysis demonstrated the non-classical nature of light so
unmistakably that physicists could no longer ignore the mysterious quan-
tum. Planck kicked off this new quantum ball game; Einstein made the
first touchdown.

Einstein's second paper explained the Brownian motion of microscopic
particles in liquids and showed how the centuries-old question of the

reality of atoms could be decided experimentally. French physicist Jean
Perrin carried out these experiments and established for the first time
conclusive evidence for the existence of atoms.

His first paper swept physicists headlong into the Quantum Era; his
second decisively settled one of the nineteenth century's biggest contro-
versies. But Einstein was just warming up.

Einstein's third paper profoundly changed our ordinary ideas of time
and space, notions that seemed so deeply embedded in human experience
as to be unquestionable. In Einstein's new vision, measurements of length
and time are not absolute but depend on the observer's velocity. For
example, two people watching the same clock see it running at different
rates if they are moving relative to each other. Other absolutes take the
place of space and time, notably the speed of light, which Einstein de-
clared to be the same for all observers. The speed of light is also elevated
to a universal speed limit which no signal can exceed. Einstein's special
theory of relativity (as he called it) had profound consequences for physics
and philosophy, for it showed that some of our most cherished notions
about the world are simply wrong and must be replaced with entirely new
ways of thinking.

Because it overturned common-sense ideas, Einstein's relativity is often
considered part of the New Physics but strictly speaking relativity belongs
to the nineteenth century. Despite its bizarre notions of space and time,
Einstein's theory does not challenge classical physics but completes it.

Classical physics is based on two sets of laws: Maxwell's field laws and
Newton's motion laws. These two sets of laws could not both be recon-
ciled with the newly observed fact that despite the Earth's motion the
velocity of light was constant in all directions. Something in classical phys-
ics had to give. Einstein kept Maxwell's laws intact but replaced Newton's
laws with his own relativistic laws of motion. These new laws make light's
speed a constant for all observers. One consequence of Einstein's revision
of Newton is his famous E = mc2 relation. Maxwell's field laws plus the
relativistic laws of motion now completely and consistently describe all
classical motion even at high velocity.

Because relativity is really part of classical physics, most physicists, once
they recovered from their initial shock, learned to accept it as a natural
extension of common sense. Despite his radical revision of space and time,
Einstein's attitude toward reality is no different from Newton's. These are
real fields here; real matter we are dealing with. Special relativity caused
no reality crisis in physics.

It is ironic that in the same year Einstein perfected the classical picture
of the world, he also began a line of thought (Einstein's first paper) which
would utterly destroy it. By his explanation of the photoelectric effect in
terms of light quanta, Einstein attacked classical physics not at some
obscure point on its fringes but squarely on center. Einstein challenged
physicists' understanding of light, a question believed to have been settled
by Maxwell before Einstein was born.

The Photoelectric Effect:
How Does Light Interact with Electrons in a Metal?

Consider a beam of light shining on a piece of metal. Classical physicists
imagined electrons in a metal as suspended in the atom's electromagnetic
field like swimmers floating in quiet waters. Light is a wave in this electro-
magnetic ocean and can knock electrons out of metal as ocean waves can
wash swimmers onto beaches. The bigger the wave, the harder the elec-
tron/swimmer is thrown out of the water.

However, photoelectric experiments don't respect this simple analogy.
For light of a given frequency, the ejected electron's energy is always the
same for the weakest light as well as for the strongest beam. When the
beam is intense, more electrons come out but they all have the same
energy. This behavior would appear very strange if it happened at the
beach: a ripple and a tidal wave (of the same frequency) would throw you
onto the sand with the same force. The tidal wave would just throw more
people out.

If you want light to give more of its energy to the ejected electron,
increasing the light's intensity is not the way to do it. Instead you must
increase its frequency. Light's energy evidently depends on its color, not
its intensity. Blue light (high-frequency) kicks electrons harder than red
light (low-frequency). Experiments say: the higher the frequency, the
greater the impact. At the beach this means that fast little ripples near the
water's edge are more dangerous—can give you a bigger jolt—than giant
low-frequency tidal waves.

Einstein explained these strange facts about light "waves" by a single
assumption. Light behaves like a shower of particles, he said, each with
energy E given by Planck's expression:

E = hf

where f is the light's frequency and h is Planck's constant of action—the
particular value Planck had to insert to calculate black-body glow cor-
rectly.

More than a century of experiments had shown light to be a wave.
Maxwell's successful theoretical description even identified what it was—
the electromagnetic field—that was making the waves. Einstein nonethe-
less demonstrated that when light interacts with metals it resembles a
shower of particles divided into "coins of energy." Taken together these
experiments indicate that, in some manner not easy to visualize, light acts
in certain situations as a wave, in others as particles.

Three wave attributes are especially discordant with the particle notion:
1. A wave can spread out over an enormous area, while a particle is con-
fined to a tiny region. 2. A wave is easily split in an infinite variety of ways,
some parts going in one direction, some another, while a particle's travel is
confined to a single direction. 3. Two waves can interpenetrate like ghosts
and emerge unchanged where particles would crash together. Particle and
wave seem irreconcilably different, but the nature of light is such that it is
able to combine these contradictory attributes in a harmonious way.

The Compton Effect:
How Does Light Interact with Electrons in a Gas?

Einstein's particles of light (dubbed "photons") showed up again in an
experiment performed by American physicist Arthur Holly Compton. In
the photoelectric effect, one photon goes in, but none come out: the
quantum of light gives all its energy to the electron. Instead of studying
light absorption, Compton studied light scattering. By shining an X-ray
beam (high-frequency light) into a gas whose electrons were loosely
bound, Compton was able to detect both the ejected electron and the
recoil photon. His experiment showed that light behaves precisely like a
little particle bouncing off the electron, provided that you assign this light
particle a momentum p according to the quantum rule:

where k is the light's spatial frequency—the number of wavelengths that
fit into one centimeter—and h is Planck's constant of action. In
Compton's experiment light acts for all the world like a tiny billiard ball,

with momentum and energy given by the magic quantum rules. You can
put in a certain frequency of light, do a billiard-ball-style calculation, and
predict where to place counters that will catch both the scattered electron
and the recoil photon. Photon in the side pocket!

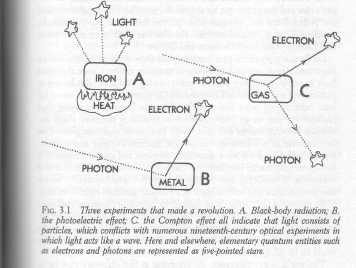
De Brogue Predicts Wave Nature of Matter

While physicists were puzzling over light's seemingly contradictory
properties, another storm was brewing in Paris. French aristocrat Louis de
Broglie had submitted a strange Ph.D. thesis to his physics professors at
the Sorbonne. By arguments that seemed dubious to his examiners, de
Broglie contended that each particle of matter was associated with a wave
whose temporal and spatial frequencies f and k were given by the Planck-
Einstein recipe E = hf and the Compton relation p = hk where E and p
are the particle's energy and momentum. De Broglie argued that just as

Einstein showed waves of light to have particle properties, so particles of
matter might also have wave properties.

Here was a delicate situation. Prince de Broglie was serious about his
proposal but his conclusion was patently absurd. His thesis professor de-
cided to send a copy to Einstein. Einstein enthusiastically backed de Bro-
glie's idea and the prince got his degree. Six years later de Broglie received
the Nobel Prize for his crazy idea. In the meantime the "de Broglie
wavelength" of a piece of matter—the electron—had been measured at
Bell Labs by Americans Davisson and Germer.

De Broglie's prophecy that matter would show wave properties was an
important step in our understanding of quantum reality. Classical physics
built its world out of two kinds of entity: matter and field (also known as
particle and wave). Planck, Einstein, and Compton showed that waves (at
least light waves) were also particles. Now de Broglie was saying that
particles are also waves. New quantum facts destroy the once sharp dis-
tinction between matter and field. With two magic quantum phrases we
can translate at will between the particle quantities energy and momen-
tum (E and p) and the wave quantities temporal and spatial frequency (f
and k), turning matter into field and vice versa. It's beginning to look as if
everything is made of one substance—call it "quantumstuff"—which
combines particle and wave at once in a peculiar quantum style all its own.

By dissolving the matter/field distinction, quantum physicists realized a
dream of the ancient Greeks who speculated that beneath its varied ap-
pearances the world was ultimately composed of a single substance. Some
philosophers said it was All Fire; some All Water. We now believe the
world to be All Quantumstuff.

The world is one substance. As satisfying as this discovery may be to
philosophers, it is profoundly distressing to physicists as long as they do
not understand the nature of that substance. For if quantumstuff is all
there is and you don't understand quantumstuff, your ignorance is com-
plete.

French physicist Oliver Costa de Beauregard calls the quarter century
from Planck's discovery of the quantum of action (1900) to Heisenberg's
formulation of matrix mechanics (1925) the Era Paleoquantique or Quan-
tum Stone Age. To explain the quantum facts during these confusing
times, physicists pieced together fragments of classical physics with cer-
tain quantum notions (notably the two magic phrases connecting wave
and particle attributes) in clever but essentially haphazard ways.

The high-water mark of Stone Age techniques was Bohr's model of the

hydrogen atom, which explained major details of hydrogen's spectrum—a
problem that classical physics could not even touch. Bohr, however, was
aware that his success was largely a matter of inspired guesswork. During
this transition period physicists lacked a reliable and consistent method—
quantum laws comparable to the classical laws of Newton and Maxwell—
of dealing with the quantum facts.

Physicists yearned for a quantum theory to lead them out of Stone Age
ignorance. The need so intense, the time so ripe, that in a single year not
one, not two, but three separate quantum theories arose where before
there had been none.

The Birth of Quantum Theory

Werner Heisenberg was first. In the summer of 1925 Heisenberg was
recovering from a hay-fever attack on the North Sea island of Heligoland.
Inspired by conversations with Bohr on the quantum mysteries, Heisen-
berg in his island retreat suddenly put it all together and came up with
matrix mechanics—the world's first quantum theory.

Quantum theory is a method of representing quantumstuff mathemati-
cally: a model of the world executed in symbols. Whatever the math does
on paper, the quantumstuff does in the outside world. Quantum theory
must contain at least: 1. some mathematical quantity that stands for quan-
tumstuff; 2. a law that describes how this quantity goes through its
changes; 3. a rule of correspondence that tells how to translate the theory's
bols into activities in the world.

Quantum Theory #1: Heisenberg represents a quantum system by a
set of matrices, hence the name matrix mechanics. A matrix is a square
array of numbers like a mileage table on a road map which lists the
distances between various cities. Each Heisenberg matrix represents a dif-
ferent attribute, such as energy or momentum, with the mileage chart's
cities replaced by particular values of that attribute. The matrix's diagonal
entries represent the probability that the system has that particular attri-
bute value, and the off-diagonal elements represent the strength of non-
classical connections between possible values of that attribute. Thus mo-
mentum p of an electron is not represented by a number as in classical
physics, but by one of these square arrays. Likewise with position x, energy
E and any other system attribute: they are all represented by matrices.

The evolution of these matrices follows a particular law of motion which
resembles Newton's law in form but contains peculiar differences. One big
difference is that unlike numbers, matrices don't commute. This means
that the order of matrix multiplication makes a difference. In particular,
when p and x are square arrays, p times x is not equal to x times p.

In the winter of 1925, Austrian physicist Erwin Schrodinger and En-
glishman Paul Dirac independently came up with two more quantum
theories.

Quantum Theory #2: Schrodinger represented quantumstuff as a
wave form and wrote the quantum laws of motion (Schrodinger's equa-
tion) such a wave form must obey. At first Schrodinger believed his waves
to be classical waves as real as Maxwell's electromagnetic vibrations, but,
as we shall see, the reality status of Schrodinger waves is extremely dubi-
ous. Because he represents quantumstuff with wave imagery, Schroding-
er's theory is called wave mechanics.

Quantum Theory #3: Dirac symbolized quantumstuff as an arrow (or
vector) pointing in a certain direction in an abstract space of many dimen-
sions. Motion of quantumstuff corresponds to rotation of that arrow. To
describe how the arrow turns, you must set up some sort of coordinates
over the arrow's space (analogous to longitude and latitude lines across the
Earth's surface) but, as on Earth, there is a great deal of freedom on how
to lay down these imaginary lines. Depending on your choice of coordi-
nates you get, for the same arrow, quantum descriptions that superficially
look very different. A big part of Dirac's theory concerns how to change
from one coordinate system to another, how to transform between seem-
ingly different descriptions of the same rotating arrow. Because of its
emphasis on switching descriptions, Dirac called his scheme "transforma-
tion theory."

Quantum physics emerged from the Stone Age with an embarrassment
of riches—three quantum theories, each claiming to explain the world. As
it turned out, all three were right. Dirac was able to show that both
Heisenberg's and Schrodinger's theories were special cases of his own
rotating-arrow version of quantum theory. Dirac's arrow looks like a clus-
ter of matrices or a wave, depending on what coordinate system you select.
Thus despite their different pictures of quantumstuff, all three theories

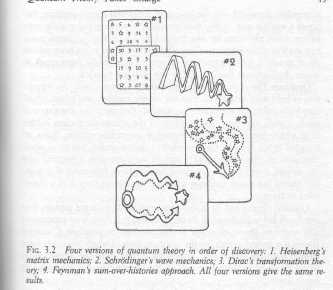
have identical content. Traveling dissimilar paths, Heisenberg, Schro-
dinger, and Dirac converged on the same explanation from three different
directions.

Why stop with three? The freedom to choose coordinates means that
quantum theory can describe the same physical situation in a variety of
mathematical languages. Physicists exploit this theory's multilingual facil-
ity by choosing, for each new problem, whatever language works best.
Physicists educated in the prequantum era favored the Schrodinger wave
picture because of its kinship with classical physics. However, young physi-
cists weaned on transformation theory soon developed a taste for abstract
languages remote from the classical tradition.

When physicists received the triple revelation from Heisenberg, Schro-
dinger, and Dirac, they began in earnest to test the new theory against
events in the outside world. At this point the story of the quantum takes
two paths: the tale of those who use quantum theory as a symbolic tool to

manipulate the world, and the history of those who regard quantum the-
ory as a window into reality, through which to perceive the world's inner
nature. Most physicists became toolmakers; few in the fast-paced quan-
tum era found the leisure to chase after "reality." Much has been written
about quantum theory's practical success in every realm from quark to
quasar. In Quantum Reality I follow the path less traveled.

Quantum Theory was invented to deal with one problem: the interac-
tion of light with atoms. But once the atomic problem was solved, physi-
cists hastened to test the new theory against other mysteries: the nature of
solids, liquids, and gases, the structure of the minuscule nucleus hidden
deep within the atom, and the nature of subnuclear entities. Some at-
tempted to see beneath the symbols to a deeper reality, but most physi-
cists used quantum theory like a pack of teenagers with a powerful new
car, driving it recklessly at top speed till something falls apart. But quan-
tum theory is a tough machine; wherever we want to steer it, this theory
takes us there.

Classical physics had its defects, experiments it could not explain, that
eventually led to its downfall. As far as we can tell, there is no experiment
that quantum theory does not explain, at least in principle. Quantum
theory is a perfect match for the quantum facts. Though physicists have
steered quantum theory into regions far distant from the atomic realm
where it was born, there is no sign on the horizon that it is ever going to
break down.

With quantum theory's unprecedented practical success and the power-
ful control over nature this success delivered, physics became big business,
an arm of the state. Reality research was soon eclipsed by an orgy of
application.

Physicists were not always so wary of reality. During the first decade of
the Quantum Era (1925-35), controversy flourished concerning the quan-
tum theory/reality connection. For instance this period witnessed the fa-
mous Bohr-Einstein debates. Gradually the view instigated by Heisenberg,
Bohr, and Gottingen-based Max Born prevailed and hardened into the
official doctrine known as the Copenhagen interpretation. Copenhagenists
claim there is no deep reality (QR # 1).

Some physicists identify Copenhagenism with pragmatism—with what
I've called the cookbook approach toward phenomena. Quantum theory is
a recipe to be compared with appearances, pragmatists say, and nothing
more. Theory tells us nothing about reality, nor should we expect it to do
so. Physics is a matter of matching mathematics to measurement; all else

is baseless speculation. Pragmatists quote Bohr approvingly: "It is wrong
to think that the task of physics is to find out how nature is. Physics
concerns what we can say about nature."

Every theory from horse-race handicap to model of the U.S. economy
possesses a minimal pragmatic core: does math fit facts? All theories are
pragmatic, at least. Some people are pragmatists because they imagine
they can avoid "philosophy" by sticking to the supposed certainties of
mathematics and experiments.

In my opinion Bohr was more than a pragmatist. He made definite
statements about the absence of a reality beneath quantum theory based
not on a distaste for philosophy but using arguments drawn from the
particular structure of quantum theory itself. All theories are pragmatic;
some theories have a reality underneath. However, quantum theory is not
a theory of this type, Bohr contends. As long as it keeps the form discov-
ered by Heisenberg, Schrodinger, and Dirac, quantum theory will never
be susceptible of reinterpretation in terms of a deeper reality.

The establishment of the Copenhagen doctrine was an important
landmark in reality research because it both represents the majority view-
point and acted to close off debate on the reality question. As CalTech
physicist Murray Gell-Mann puts it: "Niels Bohr brainwashed a whole
generation of physicists into thinking that the job was done fifty years
ago."

Two other landmarks connected with the Copenhagen interpretation
are Heisenberg's uncertainty principle and Bohr's principle of comple-
mentarity. Together they express basic restrictions which nature seems to
impose on any measurement act. We will see how Bohr uses these funda-
mental observational limits to argue that neither measurement nor theory
can put us in contact with deep reality.

Despite the extreme language of some quantum realists, no physicist
actually denies that electrons exist. You see their effect whenever you
switch on the TV. If electrons don't exist, what makes the picture on the
screen?

What's at stake in the quantum reality question is not the actual exis-
tence of electrons but the manner in which electrons possess their major
attributes. Classical physicists imagined that every particle possessed at
each moment a definite position and momentum; each field likewise pos-
sessed a particular field strength at every location. If we agree to call any
entity—particle, field, apple, or galaxy—which possesses its attributes in-
nately an "ordinary object" then the fundamental message of classical

physics was this: the entire physical world consists of nothing but ordinary
objects.

Quantum theory suggests, on the other hand, that the world is not
made of ordinary objects. An electron, and every other quantum entity,
does not possess all its attributes innately. An electron does possess certain
innate attributes—mass, charge, and spin, for instance—which serve to
distinguish it from other kinds of quantum entities. The value of these
attributes is the same for every electron under all measurement conditions.
With respect to these particular attributes, even the electron behaves like
an ordinary object.

However, all other attributes, most notably position and momentum,
which, it was thought, classical particles possessed innately, can no longer
be attached to the electron without qualification. These attributes—called
"dynamic" to distinguish them from the "static" attributes mass, charge,
and spin—do not belong to the electron in itself, but seem to be created
in part by the electron's measurement context. The manner in which an
electron acquires and possesses its dynamic attributes is the subject of the
quantum reality question. The fact of the matter is that nobody really
knows these days how an electron, or any other quantum entity, actually
possesses its dynamic attributes.

According to the Copenhagen interpretation, the electron's dynamic
attributes are contextual: what attributes it seems to have depends on how
you measure it. An electron's so-called attributes belong jointly to the
electron and the measuring device. When a Copenhagenist says, "There
is no deep reality," she means that there is no hidden value of position
that the electron "really has" when it is not being measured. Since posi-
tion is an attribute that belongs jointly to the electron and its measuring
device, when you take away the measuring device you take away the elec-
tron's position too.

An example of a contextual attribute is the color of an ordinary object.
Color is not an innate attribute but depends on the quality of illumination
and other aspects of the viewing situation. Grocers exploit the contextual
nature of the color attribute by displaying meat and vegetables under
tinted lights which render their colors more appealing than the white light
of ordinary reality. Although the color of beefsteak is not an innate attri-
bute, it is based on an attribute that is intrinsic to beefsteak—namely, this
meat's absorption spectrum. The conjunction of absorption spectrum (in-
nate to beefsteak), emission spectrum (innate to meat-counter light), and
spectral response (innate to human eye) determines the color attribute of

the steak. Change one element in this triad of innate attributes and you
change the beef's perceived color.

Is it possible that the position of an electron is like the color of a
beefsteak—that is, a contextual attribute based on deeper attributes which
are not contextual? When a Copenhagenist says, "There is no deep real-
ity," she means that the electron is not like a beefsteak: no deep innate
attributes exist which explain the electron's measurement-dependent posi-
tion and momentum. When you take away the measuring device the
electron undoubtedly still exists, but it possesses no dynamic attributes at
all; in particular it has no definite place or motion. We cannot picture
such a state of being, but nature seems to have no trouble producing such
entities. Indeed, such entities are all this world is made of.

A beefsteak's color may be contextual, but in most environments it
looks red. As long as we keep the limits of such a statement in mind we
are entitled to say that beefsteak is red. In other words color is almost an
innate attribute. But in reality it's not. Likewise, as long as we do not push
its limits an electron appears to have a definite position and momentum at
all times. The electrons in your TV tube, for instance, when they're not
forced to go through tiny holes seem to behave like classical objects. In
other words, an electron's dynamic attributes are almost innate. The enor-
mous success of classical physics depended on this fact: the entities that
make up the world are almost ordinary objects. But in reality they're not.

Von Neumann's Quantum Bible

In 1932 the eminent mathematician John von Neumann published his
definitive analysis of quantum theory. Von Neumann's Die Grundlagen
The Foundations) is our quantum bible. In this influential book von
Neumann gives quantum theory a firm mathematical basis and tackles
many reality-related issues in a highly logical manner. Von Neumann
poses the famous quantum measurement problem which, as we shall see,
lies at the heart of the quantum reality question. It is fair to say that if we
could say what actually goes on in a measurement, we would know what
physical reality was all about. Because of his peculiar views on measure-
ment, von Neumann is sometimes regarded as the godfather of the con-
sciousness-created reality school (QR #7).

In Die Grundlagen von Neumann considers the claim of the neorealists
that an ordinary reality underlies the quantum facts, and in a short formal

argument (known to reality researchers as "von Neumann's proof") con-
cludes that the existence of such a reality is mathematically incompatible
with quantum theory. Von Neumann's proof was widely regarded as con-
firming Bohr's Copenhagen party line: there is no deep reality and it is
futile to search for one.

What von Neumann showed was that if you assume that electrons are
ordinary objects or are constructed of ordinary objects—entities with in-
nate dynamic attributes—then the behavior of these objects must contra-
dict the predictions of quantum theory. Furthermore if you assume that
electrons possess contextual attributes that stem from ordinary objects
inaccessible to measurement but whose innate attributes combine "in a
reasonable way" to simulate the electron's measurement-dependent be-
havior, then these entities likewise must violate quantum theory's predic-
tions. Thus, according to the quantum bible, electrons cannot be ordinary
objects, nor can they be constructed of (presently unobservable) ordinary
objects. From its mathematical form alone, von Neumann proved that
quantum theory is incompatible with the real existence of entities that
possess attributes of their own.

For more than a quarter of a century the authority of von Neumann's
proof dampened enthusiasm for reality research. Why search for an ordi-
nary reality beneath quantum theory, when the world's top mathematician
tells you such a thing is impossible?

However, in 1952, despite von Neumann's proof, David Bohm did the
impossible by constructing a model of the electron with innate attributes
whose behavior matches the predictions of quantum theory.

Bohm's Ordinary-object Model of the Electron

Bohm was born in Pennsylvania and studied physics at Berkeley under }.
Robert Oppenheimer, who had learned quantum theory in Copenhagen
from Bohr himself. When Bohm finished his studies, he became a Prince-
ton professor and decided to clarify his thinking by writing a textbook on
quantum theory.

Bohm's textbook Quantum Theory is valued by students as a simple
introduction in plain English to the mechanics of quantum calculations as
well as for its unusually detailed discussions of the reality question. Like
his teacher and the majority of physicists, Bohm was a loyal Copenhagen-
ist. His treatment of the reality question follows Bohr's party line. In place

of von Neumann's highly mathematical injunction against ordinary real-
ity, Bohm comes to the same conclusion using informal arguments. In
Quantum Theory Bohm argues, in agreement with Heisenberg, Bohr, and
von Neumann, that electrons are not things.

In 1951 David Bohm tangled with American political reality when he
refused to testify against Oppenheimer before Senator Joseph McCarthy's
Committee on Un-American Activities. He lost his job at Princeton and
never again taught in the United States, moving first to Brazil and finally
settling in London.

At about this time, conversations with Einstein convinced Bohm that
no matter what he said in his textbook, no matter what von Neumann had
proved, an ordinary reality interpretation of quantum theory was possible.
In 1952 Bohm constructed such a model for the electron. In Bohm's
model the electron is a particle, having at all times a definite position and
momentum. In addition, each electron is connected to a new field—the
so-called "pilot wave"—which guides its movement according to a new
law of motion. Both wave and particle are real—no fictitious proxy waves
here—but the pilot wave is invisible, observable only indirectly via its
effects on its electron. In Bohm's model, quantumstuff is not a single
substance combining both wave and particle aspects but two separate
entities: a real wave plus a real particle.

The pilot wave, acting as a sort of probe of the environment, changes its
shape instantly whenever a change occurs anywhere in the world. In turn,
pilot wave communicates news of this change to electron, which alters its
position and momentum. When you make one kind of measurement, the
pilot wave has one form; when you make another kind of measurement,
this wave takes another form. For different kinds of measurement the
electron takes on different attributes, because its pilot wave is different.
Thus Bohm's model simulates the electron's contextual behavior using
entities (pilot wave plus particle) whose attributes are not contextual. The
electron's attributes are innate, but seem to be contextual because the
omnipresent pilot wave renders these attributes delicately and immedi-
ately responsive to every detail of its environment, including the type of
measurement you are preparing to make upon it.

The notion that quantum theory could be explained in terms of an
ordinary wave guiding an ordinary particle originated with Prince de Bro-
glie in the late twenties. Encountering severe mathematical difficulties, de
Broglie abandoned his model in favor of the reigning Copenhagen doc-
trine until David Bohm, a quarter century later, showed how the wave-

plus-particle concept could be made to work to produce a consistent pic-
ture of the quantum facts,

Bohm's pilot wave model revived neorealist hopes that quantum theory
might be explained in terms of ordinary objects. However, Bohm's model
is plagued with a peculiar affliction. In order for it to work, whenever
something changes anywhere the pilot wave has to inform the electron
instantly of this change, which necessitates faster-than-light signaling. The
fact that superluminal signals are forbidden by Einstein's special theory of
relativity counts heavily against Bohm's model, but he was never able to
rid it of this distressing feature. Because of its somewhat contrived nature
and the presence of superluminal influences, Bohm regarded his model as
a mere beginning, as a concrete demonstration that an ordinary reality
model of quantum reality was indeed possible. Encouraged by this initial
success, Bohm continued to look for a better picture of the reality he was
convinced lay behind the quantum facts.

Bell's Interconnectedness Theorem

In 1964 Irish physicist John Stewart Bell, working at CERN, the Euro-
pean accelerator center in Geneva, Switzerland, took sabbatical leave from
the fast-paced world of high-energy physics to explore the byways of quan-
tum reality. The first question Bell asked was: how was Bohm able to
construct an ordinary reality model of the electron when von Neumann
had proved that nobody could ever do such a thing? Bohm's model actu-
ally did what it claimed: it duplicated the results of quantum theory using
a reality made of nothing but ordinary objects. So the fault must lie not in
Bohm's model but in von Neumann's proof.

Bell carefully studied this proof in its original version and several varia-
tions which other theorists had worked out since the publication of the
quantum bible. He was able to find the loophole which permits Bohm's
ordinary reality model to exist.

Von Neumann and his colleagues had shown that any scheme in which
ordinary objects combined "in reasonable ways" could not reproduce the
results of quantum theory. Bell showed that von Neumann's notion of
reasonable ways was unnecessarily restrictive. In particular, von Neumann
would not have considered "reasonable" electrons which could adjust their
attributes via an invisible field that can sense the configuration of the
measuring device. Bohm's model, which is based on such context-adapt-

able electrons, is not "reasonable," hence it evades von Neumann's proof.
The fact that thirty years passed before this loophole was discovered is a
measure both of the authority of von Neumann and the leisurely pace of
quantum reality research.

As he examined von Neumann's proof, Bell wondered whether a truly
ironclad argument could be constructed which would set firm limits on
the sorts of realities that could underlie the quantum facts. While visiting
SLAC—Stanford Linear Accelerator Center—Bell discovered such a
proof, which has since become known as Bell's theorem. The unusual
demands Bell's theorem makes on reality gives us our clearest picture to
date of the irreducible strangeness of the quantum world.

Arguing from quantum theory plus a bit of arithmetic, Bell was able to
show that any model of reality whatsoever—whether ordinary or contex-
tual—must be non-local. Bell's theorem has since been proved entirely in
terms of quantum facts; no reference to quantum theory is necessary. In
its most up-to-date version Bell's theorem reads: The quantum facts plus a
bit of arithmetic require that reality be non-local. In a local reality, influ-
ences cannot travel faster than light. Bell's theorem says that in any reality
of this sort, information does not get around fast enough to explain the
quantum facts: reality must be non-local.

Suppose reality consists of ordinary objects which possess their attri-
butes innately. Bell's theorem requires for such a world that its objects be
connected by non-local influences. Bohm's model is an example of such a
world. In this model an invisible field informs the electron of environmen-
tal changes with a superluminal response time. Bell's theorem shows that
the faster-than-light character of Bohm's pilot wave is no accident. With-
out faster-than-light connections, an ordinary object model of reality sim-
ply cannot explain the facts.

Suppose reality consists of contextual entities which do not possess attri-
butes of their own but acquire them in the act of measurement, a style of
reality favored by Bohr and Heisenberg. Bell's theorem requires for such
entities that the context which determines their attributes must include
regions beyond light-speed range of the actual measurement site. In other
words, only contextual realities which are non-local can explain the facts.

Bell's theorem proves that any model of reality, whether ordinary or
contextual, must be connected by influences which do not respect the
optical speed limit. If Bell's theorem is valid, we live in a superluminal
reality. Bell's discovery of the necessary non-locality of deep reality is the

most important achievement in reality research since the invention of
quantum theory.

Though motivated by quantum theory, Bell's theorem has deeper roots.
Von Neumann's proof, for instance, depends on the truth of quantum
theory; Bell's theorem does not. As we shall see, to prove Bell's theorem all
you need are the facts plus a little arithmetic. The relevant facts are not in
question; John Clauser measured them at Berkeley in 1972. Though
today's quantum theory shows no sign of weakness, someday it may col-
lapse. Bell's theorem will survive its demise and impose non-locality on
quantum theory's successor. Because Bell's theorem makes contact with a
general feature of reality itself, it foretells the shape of all future physical
theories.

Feynman's Version of Quantum Theory

In the late forties, while Bohm was writing his popular textbook on the
Copenhagen interpretation, Richard Feynman, then a professor at Cor-
nell, discovered a fourth version of quantum theory called the "sum-over-
histories" approach. Although it makes the same predictions as the other
three quantum theories, the Feynman variation is more than just another
language and cannot be reached by a Dirac transformation. It is a funda-
mentally new way of looking at quantum theory.

Quantum Theory #4: Heisenberg represented it as a matrix, Schro-
dinger as a wave; Feynman represents quantumstuff as a sum of possibili-
ties. Everything that might have happened influences what actually does
happen. Feynman's quantum possibilities are different from classical prob-
abilities. Classically the more ways an event can happen, the more proba-
ble its occurrence. In quantum theory, possibilities have a wavelike nature
that allows them to cancel, so increasing the number of quantum possibili-
ties does not always make an event more probable.

To calculate an electron's fate, Feynman adds up all its possible histo-
ries. In the peculiar quantum manner, many histories will cancel. What-
ever is left represents what will actually happen—expressed as a pattern of
probabilities.

Feynman's sum-over-histories approach is particularly useful for carrying
out complex quantum calculations. To predict what will happen in a par-
ticular situation, a theorist ranks classes of possible histories in terms of

their relative importance and adds the biggest ones first. To keep track of
which histories have already been summed, Feynman invented the cele-
brated Feynman diagrams. Each diagram is shorthand for an entire class
of possible histories. So pervasive are the Feynman hieroglyphs that in-
stead of talking about "summing over histories," physicists usually speak
of "summing over diagrams."

My exposition of quantum theory in Chapter 6 is inspired largely by
Feynman's picturesque sum-over-histories approach. Feynman's way of do-
ing things is original and daring. At a recent conference, Feynman's col-
league Freeman Dyson recalled his first impressions of this unusual ap-
proach to quantum theory: "Thirty-one years ago, Dick Feynman told me
about his 'sum over histories' version of quantum mechanics. The elec-
tron does anything it likes,' he said. It just goes in any direction, at any
speed, forward or backward in time, however it likes, and then you add up
the amplitudes and it gives you the wave function.' I said to him 'You're
crazy.' But he isn't."

This account of the highlights of quantum reality research is necessarily
brief and incomplete. For the reader in search of more detail, I recom-
mend Max Jammer's excellent book The Philosophy of Quantum Mechan-
ics.

Physicists did not willingly give up ordinary reality to wallow in dozens
of bizarre and contradictory pictures of the world: experiments pushed
them into the quantum soup. We turn now to those persuasive experi-
ments, physicists' court of last resort, the troublesome quantum facts.

4 - Facing the Quantum Facts

"I remember discussions with Bohr which went through many
hours till very late at night and ended almost in despair, and when
at the end of the discussion I went alone for a walk in the neigh-
boring park I repeated to myself again and again the question:
"Can nature possibly be as absurd as it seemed to us in these
atomic experiments?"

---Werner Heisenberg

Physicists, for all their odd notions, are basically a conservative lot. They
would have been content, most of them, to dwell in the solid classical
world created by the great scientists of the Victorian Era and leave wild
speculations concerning the nature of things to the science fiction chroni-
cles of Jules Verne. However, new quantum facts forced physicists to
admit that the world almost certainly rests on some bizarre deep reality. If
scientists routinely contact facts which reveal such outlandish realities, life
in a modern physics lab must be pretty unusual.
One imagines Max, the famous quantum physicist, deciding on Mon-

day morning to face the quantum facts. Donning quantum-resistant body
armor, he climbs inside his bubble chamber, waves goodbye to the worka-
day world, and prepares to enter the mysterious realm of the quantum.
Alone in the dark, Max checks his life-support system and the crucial
flyback circuit that returns him to ordinary reality. Then, taking a deep
breath, he pulls the switch.

Max suddenly drops through the world's phenomenal surface into deep
quantum reality. Holy Heisenberg! Centuries of Newtonian certainties
vanish in an instant. Solid objects melt into the undivided wholeness as he
enters the Place Without Separation. Max mixes with the mystery when
his subject/object membrane dissolves. In tune with totality, Max creates
a new universe faster than light wherever he turns his omnipotent gaze.

What's it like down there? Max's sister Maxine says it feels just like
Schrodinger's equation, only more so. You've got to see it to believe it.
Behind the high-security fences of Max's quantum lab, consciousness cre-
ates reality, quantum logic is spoken exclusively, and for the trip home you
have your choice of a billion different universes.

Cinderella Effect: The Ordinariness of Quantum Facts

Sad to say, physics labs are not so exciting. Despite the outlandish realities
invented to explain them, quantum facts consist of quite ordinary events;
these quantum experiments are remarkably commonplace, especially when
compared with the extravagant claims of the quantum realists. Even our
clearest factual window into deep reality—the celebrated EPR experiment
which validates Bell's interconnectedness theorem—is, as we shall see,
absolutely ordinary.

All quantum experiments consist of commonplace events, a fact I call
the Cinderella effect. The world may really be as strange as some physi-
cists say, but it does not flaunt this strangeness, evidently preferring to
hide its magic—like Cinderella—in humble guise. The Cinderella effect
itself is a subtle example of quantum weirdness: why does nature employ
such extraordinary realities to keep up merely ordinary appearances?

Niels Bohr in his Copenhagen interpretation of quantum theory gave
prominent place to the Cinderella effect when he insisted that all quan-
tum experiments be described in ordinary—Bohr called it "classical"—
language:

"However far the phenomena transcend the scope of classical physical
explanation, the account of all evidence must be expressed in classical
terms . . . The account of the experimental arrangement and of the re-
sults of observation must be expressed in unambiguous language with
suitable application of the terminology of classical physics."

In other words, although the explanation of quantum facts is far from
ordinary, the facts themselves are made from the same kinds of events as
prequantum facts—unit acts as unremarkable as those of everyday life.
Bohr was one of the few quantum theorists to emphasize the ordinariness
of quantum fact. Bohr believed that ordinariness is built into human
modes of perception so that all future quantum facts would likewise be
ordinary. Humans are fated to experience the quantum world secondhand:
we will never, like Max, enjoy direct experience of quantum reality.

Sixty years of experiments agree with Bohr. Today's state of the quan-
tum art is such that we cannot directly experience quantum reality. All
human experiences—or at least all physics experiments—are ordinary, not
quantum, in appearance. Whether our reliance on classical modes of per-
ception is a permanent feature of the human condition remains to be
seen. We humans are ingenious animals, perhaps too ingenious for our
own good. Since "reality has consequences," we might anticipate that if
one of these quantum realities is "really real," we will eventually figure out
how to experience it directly: Max's bizarre quantum lab may not be so
farfetched in the future. Now, we see quantum reality through a glass
darkly, but then, face to face. However, since all of today's quantum facts
are admittedly ordinary, what basis do physicists have for their outrageous
claims regarding deep reality?

Quantum facts are indeed ordinary. But quantum theory—the only
complete explanation we possess of these facts—is decidedly non-ordinary.
Since quantum theory fits the facts exactly, many physicists are sure that it
bears some relationship to reality itself: such a perfect match between
theory and fact is no accident. Physicists come up with different pictures
of quantum reality depending on what aspects of quantum theory they
decide to take seriously and which parts they discard as mere mathemati-
cal figures of speech.

Quantum reality doesn't show up directly in the quantum facts: it
comes indirectly out of the quantum theory, which perfectly mirrors these
facts. Before examining this theory which supports so many odd realities,
let's take a look at some of the facts it so successfully explains.

The simplest conceivable quantum experiment consists of a source of
quantumstuff, a quantumstuff detector, plus something to put in between
that alters quantumstuff in a systematic way.

Testing a Quantum Entity

As a typical quantum entity I choose the electron, the first "elementary
particle" to be discovered—by Englishman Joseph J. Thomson in 1897.
Despite modern attempts to split it into finer bits, using energies a hun-
dred billion times greater than those that hold the atom together, the
electron remains steadfastly elementary. An electron, so it seems, simply
doesn't have any parts.

Inside a TV set, astronomical numbers of electrons detect, decode, and
display information carried into your home via electromagnetic waves vi-
brating ten million times slower than waves of visible light. The heart of a
TV set is its picture tube.

Inside the picture tube, a beam of electrons paints a new TV image on
the phosphor screen sixty times a second. For our quantumstuff source and
detector, we will borrow from a picture tube its electron gun and phosphor
screen.

The electron gun contains a metal filament heated to boil off electrons,
and some charged metal cylinders which accelerate them to high veloci-
ties. A TV electron gun—about six inches long—is a miniature linear
accelerator. Inside a color TV, electrons strike the screen with an energy
of about 25 thousand volts. Electrons in Stanford's two-mile-long linear
accelerator attain energies a million times greater.

Knobs behind your TV set control the action of the electron gun.
When we remove the electron gun for our quantum experiment, we will
also take two of these knobs: the brightness control, which varies the
intensity—electrons per second—of the beam; and the high voltage con-
trol, which varies the electron's momentum—how fast it's moving when it
strikes the phosphor screen.

The active ingredient of the phosphor screen is a solid substance—the
phosphor—ground to the consistency of face powder, mixed with glue,
and spread thin against the back of the glass faceplate. As its name im-
plies, a phosphor is a molecule that gives off light. A phosphor molecule
usually resides in its "ground state"—its state of lowest energy, symbolized
by P. When a phosphor gains energy—by being hit by a fast electron, for

instance—it transforms into an "excited state," symbolized by P* (pro-
nounced "P star"):

P + Energy -->P*

The phosphor doesn't stay in this excited state for long. It wants to get rid
of its excess energy and return to its ground state. For a phosphor, the
easiest way to lose energy is to emit a photon of light:

P* -->P + light

Now the phosphor is back in its ground state, ready to be excited again,
and some of the electron's energy has been converted to light. The overall
action of a phosphor looks like this:

P + Energy --> P + light

Just as a chemical catalyst facilitates chemical reactions without being
itself changed or used up, so a phosphor is a kind of energy catalyst
remaining unchanged as it turns some of an electron's kinetic energy into
light.

Phosphors are particularly useful as quantum detectors because they are
sensitive enough to respond to a single quantum (in this case an electron)
and are not particular about where their excitation energy comes from. A
phosphor glows when struck by electron, but proton, pion, or any other
charged particle will do as well. A phosphor can even be excited by light—
that is, by a photon. Turning light into light may not seem very practical,
but makes sense if the input light is invisible—infrared or X rays, for
instance. Phosphors that turn invisible radiation into visible light make
good X-ray viewing screens.

A phosphor can be excited by as little as one volt of energy. A quantum
particle carrying several thousand volts can excite many phosphor mole-
cules, which appear as a bright flash easily visible to the naked eye.
Phosphors are sensitive, fully reusable quantum detectors which signal the
presence of a quantum particle with a flash of light. So that we can discuss
the quantum measurement process in an orderly fashion, all my detectors
use phosphor molecules as their primary sensors.

The Electron's Particle Nature

For our first quantum experiment, we aim the electron gun at the phos-
phor screen and observe a small dot of light where the beam strikes the
screen. The intensity of this dot goes up as we increase the number of
electrons by turning up the brightness or as we increase the electron
energy by turning up high voltage. As we manipulate these controls, the
spot size remains the same.

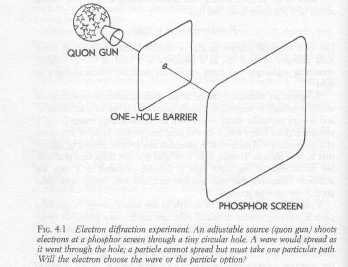
Turning down brightness decreases the spot's intensity. At low-beam in-
tensity, we can see the effect of the individual electrons which make up
the beam: the spot does not shine constantly now but sparkles as each new
electron excites a clump of phosphors. At very low brightness we can
watch the arrival of single electrons as they strike the TV screen. This

experiment gives tangible evidence for the electron's particle nature: elec-
trons are particles because you can count them.

How small are these little particles of electricity? Physicists have at-
tempted to determine the electron's size by using another electron as a
probe. Two electron beams are accelerated, then bent with magnets so
they meet head on. Electrons don't actually have to touch in order to
interact, because each one is surrounded by its own electric field. At large
separations electrons scatter via these fields. Physicists hope to measure
their intrinsic size by pushing them closer and closer together (by increas-
ing the accelerator energy) until deviations from pure-field scattering oc-
cur, indicating that the electrons themselves are beginning to touch.

Present-day accelerators can probe distances as small as 10[to the16 power of] cm—a
thousand times smaller than a proton's diameter. At these tiny separa-
tions, electrons still show nothing but pure-field scattering. If the electron
has any size at all, it is smaller than we can measure. Some physicists
conjecture that the electron is a point particle whose intrinsic size is zero!
All truly elementary particles, they imagine, are likewise mathematical
points. Only composite entities such as atoms, built up of elementary
particles, will show a structure or have a definite size. None of the current
candidates for elementarity—i.e., quarks, leptons, or gluons—shows any
detectable structure, which agrees so far with this point-particle conjec-
ture.

Electron is an example of quantumstuff which possesses both wave and
particle properties. The diameter of the electron-as-particle is very small: it
may be zero. We can actually "see" these electron "particles" arriving one
at a time on the TV screen; evidence for the electron's particle nature is
clear and indisputable. Next we look at the evidence for its wave nature.

The Electron's Wave Nature

As our "wave probe" we insert a small circular iris between the electron
gun and the luminescent screen, positioning it so that the electron beam
goes through the hole. We make the hole smaller, squeezing down on the
electron beam. At first the electron beam gets smaller as the hole shrinks,
as shown by the smaller spot on the screen. However, beyond a certain
point the spot refuses to shrink and actually begins to get larger. As we
continue to decrease the iris size, the image on the phosphor screen ex-

pands until it is no longer a spot but a series of bright and dark rings
resembling an archery target.

When we contract the hole further, this target figure enlarges, its bulls-eye
expanding to fill the entire screen, till finally—when the iris is very small

—the screen is covered with a uniform glow. As the hole continues to
contract, the phosphor screen remains uniformly illuminated but the light
intensity decreases. Finally, when the hole closes completely, the screen
goes dark.

We open the iris again, adjusting it so the electrons reform the target-

Notice that this formula describes an inverse relation between hole size d
and the angular size of the bull's-eye 6 agreeing with the experimental
observation that the pattern gets bigger as the hole shrinks. We also see
that when the hole is the same size as the wavelength, Airy's disc subtends
an angle of 70 degrees, a fact which allows us to calculate the wavelength
of the electron from the size of the Airy pattern.

Airy didn't have electrons in mind when he did his calculation—they
were yet to be discovered. He was trying to explain the pattern that light
makes when it goes through a small hole. You can see the optical Airy
pattern for yourself by punching a tiny hole (0.1 mm) in a piece of alumi-
num foil, holding it up to your eye and viewing a point source of light (the
sun's too big) such as a distant streetlamp.

In the nineteenth century, Airy's explanation of this pattern as a signa-
ture of wave action provided a key piece of evidence for the wave nature
of light. One hundred years later, physicists regard the electron's Airy
pattern as twentieth-century evidence for the wave nature of matter.

An electron seems to possess contradictory attributes. As a particle, it
must be localized in space, cannot be split apart, and retains its identity in

collisions with other particles. As a wave, it spreads over vast regions of
space, is divisible in an infinity of ways, and merges completely with other
waves it happens to meet.

A purely particle theory cannot explain the Airy pattern; a purely wave
theory cannot explain the flashes on the screen. The electron is in reality
neither particle nor wave, but an entity entirely new to human experience
which exhibits the properties of both. The electron is pure quantumstuff.

We've carried out this experiment with electrons, but every other quan-
tum entity behaves the same way. Photons, quarks and other elementary
particles will likewise show an Airy pattern built of little flashes if you put
them through a tiny hole. To see their quantum nature, merely replace the
electron gun with one that shoots photons or quarks.

Most physicists believe that ordinary objects—baseballs, tomatoes,
Mack trucks—would in principle exhibit quantum wave properties under
the right conditions, but their extremely short de Broglie wavelengths
make such effects impossible to observe in practice.

Everything in the world is pure quantumstuff, a physical union of parti-
cle and wave. The particle aspect of light waves is called "photon"; the
particle aspect of gravity is called "graviton"; the particle aspect of the
strong nuclear force is called "gluon." No term exists for a generic quan-
tum object. I propose the word "quon." A quon is any entity, no matter
how immense, that exhibits both wave and particle aspects in the peculiar
quantum manner.

What's an experiment without knobs to wiggle? Let's see what happens
to the Airy pattern as we change the electron gun's high voltage and
brightness controls.

First the high voltage control. As we turn up the voltage, the Airy
pattern gets smaller, eventually shrinking back down to a tiny spot. Turn-
ing down the voltage makes the pattern expand. Evidently the high volt-
age control affects the electron's wavelength: the higher the voltage, the
shorter the wavelength. In a TV tube, high voltage corresponds to high
electron momentum. We can use the observed variation in Airy pattern
size with voltage to discover the relationship between the electron's mo-
mentum and its wavelength. For each high voltage setting, we calculate
the electron's wavelength L from Airy's formula and the observed size of
the Airy disc. The electron's momentum p is related to its voltage by a
well-known classical formula. The experimental relation obtained in this
TV-based diffraction experiment between an electron's momentum and
its wavelength is particularly simple:

p = h/L

where h is a constant which appears in almost every quantum relation—
Max Planck's ubiquitous constant of action.

Expressed in terms of spatial frequency k rather than wavelength L, this
relationship becomes:

p = hk

Whether to express the electron's wave aspect in terms of wavelength or
spatial frequency is a matter of convenience. What's important is that
these electron diffraction experiments demonstrate an extremely simple
connection (involving Planck's constant) between the particle property
momentum and a property (wavelength or spatial frequency) heretofore
associated only with waves.

This notion that the electron, then considered a mere particle, also
possessed wave aspects was first proposed by French physicist Louis de
Broglie in 1924. De Broglie predicted the above momentum/wavelength
relation, which was subsequently verified by Americans Davisson and
Germer in electron diffraction experiments similar in principle to our one-
hole TV display.

Are Electron Waves "Crowd Waves"?

The fact that the electron shows both wave and particle properties is not
in itself peculiar. What's strange is how these properties coexist. We don't
find it remarkable that water waves consist of particles—molecules of
water—that collectively behave like a wave. Sound is another example of a
wave riding on a collection of particles. I call such waves made of particles
"crowd waves." To make a crowd wave, many molecules must be packed
together. A bell ringing in a sealed jar makes no noise when there's not
enough air inside to support sound waves.

The crucial test for crowd waves is dilution. We can make a crowd wave
disappear by decreasing the number of molecules in the crowd. Pumping
the air out of the jar silences the bell.

We dilute our electron beam by turning down the brightness. First
adjust all controls for a big clear Airy pattern. Then reduce the brightness.
Will the Airy pattern go away once the number of electrons gets small,
revealing the electron wave to be a mere "crowd wave"? Don't bet on it.

As we turn down the brightness, the number of electrons striking the
screen decreases. Glow turns to sparkle, breaking up gradually into individ-
ual flashes. Finally only about one electron per minute hits the TV screen.
At this low brightness, most of the time the TV tube is empty. Certainly
this drastic electron deficit has eliminated any possibility of crowd waves.
But it's also eliminated the Airy pattern. All we see on the screen is a
single flash every minute or so.

To record possible long-term patterns in these isolated flashes, we press
a piece of photographic film against the glass. A few weeks later we return
and develop the film. The first physicist to perform this kind of quon-
dilution experiment, Englishman G. I. Taylor, went sailing on the Thames
while his flashes accumulated. Returning to the lab, we develop the film.
We see thousands of dots, each a token of a single electron. But rather
than being scattered at random, they form exactly the same Airy pattern
as the high-intensity beam. Electrons evidently behave like waves no mat-
ter how much you dilute them. Electrons are definitely not crowd waves
like sound and surf.

This quon dilution experiment shows that, although it appears on the
screen as a particle, each electron by itself travels from gun to screen as
though it were a wave. The electron manages its contradictory aspects by
assuming them one at a time. Whenever it's being observed, an electron
always looks like a particle—and a mighty small one at that. In between
observations, the same electron spreads out like a wave over large regions
of space. This alternation of identities is typical of all quantum entities
and is the major cause of the reality crisis in physics.

Wave/Particle Coexistence

The world is made entirely of quons that behave like this electron. How
shall we explain such an entity? It acts like a particle whenever we look. In
between looks it acts like a wave. Because measured electron is radically
different from unmeasured electron, it appears that we cannot describe
this quon (or any other) as it is without referring to the act of observation.
If we ignore observations for the moment, we might be tempted to say
that an electron is all wave, since this is how it behaves when it's not
looked at. However this description ignores the massive fact that every
observation shows nothing but little particles—only their patterns are
wavelike. If we say, on the other hand, that between measurements the

electron is really a particle, we can't explain the quantum facts. How does
each electron on its own know how to find its place in the (wavelike) Airy
pattern? What does a single electron "interfere with" to produce Airy's
dark rings?

The essential difficulty in describing quantum reality is that unmea-
sured quons seem to behave in a totally different manner from measured
quons, and that neither behavior by itself is enough to explain how the
world itself behaves. Quantum realists would like to be able to give a single
description of the world as it is, independent of how it seems when we
look at it. Of course such a description should explain how the world
appears when measured, but the measurement act should be a subordinate
part of any model of reality, not an essential feature.

However, the quantum facts give us not one description but two—each
one separately inadequate, and both together contradictory. Moreover the
knot that connects these two descriptions is the act of observation; leave
out observation and neither description makes sense.

Physicists customarily appeal to experiment to settle matters of princi-
ple. Using a TV tube, we looked at some of the electron's peculiar quan-
tum properties. Certainly there must be other experiments we could do
that would tell us more than we could learn from this single setup. Per-
haps by making other kinds of measurements we could learn what the
electron's actually doing in the TV tube when it's "unobserved."

The Uncertainty Principle Protects Wave/Particle
Coexistence

Whenever we perform other experiments we indeed get new information,
but it's never enough to solve this problem. All experiments show the
same kind of unmeasured wave, measured particle duality. An instrumen-
tal barrier seems to exist which prevents probing the quantum world deep
enough to resolve the wave/particle question in favor of one or the other
modes of being. Too close scrutiny of a quon's behavior is blocked by the
distinctively quantum feature of conjugate attributes.

In classical physics, all of an entity's attributes are in principle accessible
to measurement, with a precision limited only by the experimenter's inge-
nuity. A quon's measurement situation is quite different. You can measure
a single quantum attribute as accurately as you please, but such a measure-
ment inevitably produces imprecision in some other quantum attribute.

For the Airy experiment, the mutual spreads in precision of these two
conjugate attributes is equal to Planck's constant. The Airy experiment is
an example of a perfect quantum measurement. It represents the most
anyone can find out about both the sidewise position and the sidewise
momentum of an electron beam.

The flavor of the strange quantum world permeates these simple experi-
ments. It's a world that's wavelike when unobserved, particlelike upon
observation: a world whose attributes come in pairs which jointly resist
close examination. Quantum theory accounts for these facts and many
more. However, rather than resolving the quantum reality question, quan-
tum theory merely deepens it.

Quantum theory, because it precisely mirrors the quantum facts, pos-
sesses the same qualities that prevent us from building a consistent ob-
server-free picture of reality from the quantum facts. In addition quantum
theory brings puzzling features of its own (wave function collapse and
phase entanglement, for instance) whose relation to what really goes on in
the world is highly dubious.

Running parallel to the quantum facts, quantum theory represents un-
measured quons as waves and measured quons as particles. Furthermore it
regards these unmeasured waves not as real waves but merely as waves of
probability. On account of its indirect method of representation, this the-

ory, highly successful in practice, seems farther removed from reality than
the experiments it so accurately predicts. However, barring a sudden
breakthrough into Max's direct way of contracting quantum reality, quan-
tum theory is the best clue we possess concerning the real nature of the
world we live in.

So we can better appreciate the probability waves with which quantum
theory characterizes the world in its unmeasured state, I review in the next
chapter some familiar properties of ordinary wave motion.

5 - Wave Motion:
The Sound of Music

"The clocks on the tower of the Ferry building said that it was 5:15
—they were running a little fast. But it was to be months before
those hands moved any farther, for at that instant the earthquake
struck . . . Jesse Cook, who was later to become police commis-
sioner, remembered hearing a deep rumbling in the distance, "deep
and terrible" in his words. And then looking up Washington
Street, he actually saw the earthquake coming. "The whole street
was undulating. It was as if the waves of the ocean were coming
toward me, and billowing as they came."

---William Bronson, reporting on the
San Francisco earthquake

Using ordinary waves in unusual ways is the secret of quantum theory.

All waves, no matter how exotic, are built on a common plan and take
their orders from the same rulebook. Although physicists connect quan-
tum waves with facts in an innovative way, the quantum waves themselves
follow the same old-fashioned rules as waves in your bathtub. In this

chapter I look at fundamental behavior common to all waves. Later we'll
examine this same behavior in waves of quantumstuff.

Waves take their character from what's doing the waving: water and air
are waving in the case of surf and sound. According to James Clerk Max-
well, light is a vibration of electric and magnetic fields. Quantum waves, as
we shall see, are oscillations of possibility.

Since a wave vibrates both in time and space, to follow it we must keep
track of two kinds of motion. One way to do this is to make two separate
pictures—one in which we stand still in space watching the wave change
in time; the other in which time stands still and we look at how the wave
changes in space. We freeze time to get a wave's spatial picture; we freeze
space to get its temporal picture.

A wave's fundamental scale is its amplitude, which measures the devia-
tion of its physical variable from the rest state. Another important wave
measure is intensity, which is proportional to amplitude squared. For all
waves except quantum waves, intensity measures the amount of energy a
wave carries at every point. Quantum waves carry no energy at all; for this
reason they are sometimes called "empty waves." A quantum wave's in-
tensity (amplitude squared) is a measure of probability.

A wave takes any form it pleases: some waveforms are one of a kind,
others are oscillatory—a parade of identical shapes like a modern produc-
tion line. Oscillatory waves go through cycles in time and space; their
essence is repetition. The time an oscillatory wave takes to go through one
cycle is called its "period." Cycle time can also be expressed in terms of
frequency: the number of cycles completed in a certain time. Period P and
frequency f are equivalent names for the rapidity of a wave's pulsations in
the temporal picture.

The space an oscillatory wave spans as it carries out one cycle is called
its wavelength. Cycle length can also be expressed in terms of spatial
frequency: the number of cycles filling up a certain distance. Wavelength
L and spatial frequency k are equivalent names for the repetition rate of a
wave's undulations in the spatial picture.

Phase is another important measure of an oscillatory wave. Each point
on a wave possess a definite phase which tells how far that point has
progressed through the wave's basic cycle. The term "phases of the moon"
expresses this same meaning of "phase" as part of a cycle. The phase of a
wave governs what happens when two waves meet. Wherever waves of the
same frequency (spatial or temporal) come together with identical phases,

they are said to be "in phase"; waves whose phases differ by half a cycle
are "out of phase."

Superposition Principle

The meeting of two waves to make a new wave may look complex but
what actually goes on is remarkably simple: the new wave's amplitude at
every point is just the sum of the amplitudes of each separate wave. When
waves meet, their amplitudes add. The fact that waves everywhere form
such uncomplicated unions is called the "superposition principle." This
principle works not just for oscillatory waves but for all waveforms whatso-
ever.

Ordinary waves obey the superposition principle for small amplitudes,
but not when amplitudes get big. Failure of the superposition principle is
called non-linearity, and shows up as distortion in hi-fi systems and as
turbulence in water waves. A remarkable feature of quantum waves is that
they seem to obey the superposition principle without restriction: no mat-
ter how complex the circumstances, the amplitudes of quantum waves
add, and nothing more. When you get down to the quantum level, wave
behavior is simpler than waves in your bathtub.

The superposition principle guarantees that when waves come together,
nothing is added or taken away. In particular, when a wave exits such a
relationship it takes with it precisely the amplitude it had when it went in.
Two waves can cross paths, form a momentary superposition, then con-
tinue on their ways entirely unchanged by their encounter—an option not
generally available to other forms of being.

Consider a sunny window. Light from many different directions crosses
as it goes through the glass. If the passage of light waves through one
another changed them in any way, the information they carry would be
distorted. Yet, because light waves interact in a "reasonable" way, the
scene outside never blurs no matter how bright the light. The superposi-
tion principle applied to light waves keeps your windows clear.

Because quantum theory in a certain sense regards the world as made
out of waves rather than out of things, quantum entities and their attri-
butes combine according to the rules of wave addition rather than the
rules of ordinary arithmetic. The superposition principle, which governs
how waves add, is as important for the quantum world as arithmetic is for
everyday life.

When two waves with equal amplitude come together, the amplitude of
the combined wave can be anywhere between zero and twice the ampli-
tude of a single wave. The critical factor which decides the outcome of
this peculiar wave arithmetic is the waves' relative phase.

Phase is a matter of timing: how soon will the next wave peak get here?
These simple examples show the importance of the phase variable for
wave addition. If two waves arrive on time, the surf is two feet high; if one
wave is half a cycle late, the ocean is mysteriously calm.

This ability of two waves to augment or diminish each other depending
on their phase difference is called interference: a particularly unfortunate
choice of words since the superposition principle assures us that the one
thing waves do not do is "interfere." Like customers making bank depos-

its, waves add or subtract their amplitudes with complete indifference to
another wave's presence. A word which does not suggest hindrance, such
as "concurrence," might have been a better choice but several hundred
years of tradition have sanctified "interference" as the official name for
the phase-sensitive union of oscillatory waves.

The extreme case of waves meeting precisely in phase to achieve maxi-
mum enhancement is called "constructive interference." Out-of-phase su-
perposition is called "destructive interference."

Destructive interference finds practical use in anti-reflective coatings of
camera lenses. Some of the light striking a lens always reflects back. Re-
flections at every glass-air interface in today's multielement lenses would
result in serious light loss and many extraneous images. These reflections
are reduced by coating each glass surface with a transparent film just a
quarter wavelength thick. Now light reflects at two interfaces—where the
coating meets the air and where it meets the glass.

It may seem that doubling the number of reflective surfaces will only
make matters worse, but destructive interference comes to the rescue.
Each new surface, because of its critical spacing, produces a wave which is
out of phase with the original reflection. In practice, complete destructive
interference can be achieved for only one color. The other colors, dimin-
ished but not destroyed, give coated lenses their distinctive purple sheen.

Wave Energy

The largest recorded tidal wave—more than 200 feet high—appeared at
Valdez, Alaska, in 1964. Four-foot breakers are not uncommon at the
beach. Was the great wave of Valdez only fifty times more powerful than
everyday surf?

A wave's amplitude measures how big it is, but grossly underestimates
the wave's destructive power. A wave's external effect depends on the
energy it carries, which is proportional to the wave's intensity (amplitude
squared). Wave energy goes as amplitude squared. When you double a
wave's amplitude, you quadruple its energy content.

Although a quantum wave possesses no energy, its intensity (amplitude
squared) does not lack a physical interpretation. For any quantum wave,
amplitude squared means probability. All that we learn here about the
energy carried by an ordinary wave is directly applicable to the probability
carried by a quantum wave. A common feature of energy and probability

Random Phase Wave Addition

In addition to adding waves in and out of phase, we could imagine adding
them with no regard to phase. A random phase results when a wave's
timing fluctuates during the course of the measurement. Since random
phase addition involves a disorderly mixture of all possible phases, we

Two unit amplitude waves added together with random phases give a
combined wave whose amplitude is the square root of two (about 1.4).

As before, let's investigate how the energy behaves during wave super-
position. Each unit wave brings in one unit of energy—a total of two units
for both. The energy output is just the combined amplitude squared,
which is also two energy units. Two units in; two units out. For random
superposition of waves, energy is exactly conserved.

When two waves meet they form a zebra-striped interference pattern
consisting of alternating regions of constructive and destructive interfer-
ence. In regions of c-interference, more energy appears than each wave
brings in; in regions of d-interference, less energy appears than each wave
brings in. In an interference pattern, local energy is not conserved: there's
too much energy in the c regions and too little in the d regions. However,
if we check the accounts carefully we find that no energy is gained or lost
overall: energy missing from the d regions exactly matches the energy
excesses in the c regions. Although it redistributes wave energy in an
inequitable way, wave interference, like every other physical process, obeys
the law of (total) energy conservation.

The Airy experiment shows a typical interference pattern: the Airy
pattern's central peak and bright circles are regions of excess energy; its
dark rings are regions of energy deficit. More energy flows from the hole
into the dark rings than ever reaches the screen: wave energy heading in
that direction cancels out by destructive interference. Fig. 5.1 shows the
Airy pattern as an alteration of in-phase and out-of-phase wave addition.
To see local energy conservation in action, we arrange to randomize the
phases of the electrons in the Airy experiment. Instead of the zebra-stripe
alternations of energy surpluses and deficits, energy is everywhere con-
served. The peaks of the Airy pattern are laid low; its valleys are exalted.
The interference pattern changes into a featureless blur. Note, however,
that although interference is destroyed by phase randomization, diffrac-
tion is not: the pattern spreads out to the same extent as before. The
ability of a wave to bend around corners does not depend on its phase.

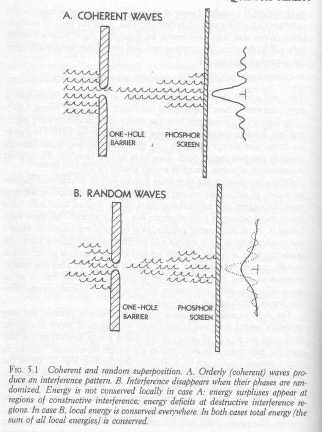
When ordinary waves superpose with definite phases, energies do not
add everywhere. When these same waves superpose with random phases,
energies add everywhere.

When quantum waves superpose with definite phases, probabilities do
not add everywhere. When quantum waves add with random phases,
probabilities add everywhere. In Chapter 8 we will see that some physi-
cists believe that the qualitative difference between random and coherent
wave addition has important consequences for where one should draw the
boundary line between quantum and ordinary reality.

Fourier's Theorem

In 1798 Joseph Fourier, a talented French mathematician, accompanied
Napoleon on his Egyptian adventure. He served for two years as governor
of southern Egypt and in 1801 returned to France with a copy of the
Rosetta stone. Examining the stone in Fourier's study, twelve-year-old
Jean Frangois Champollion was fascinated by its mysterious picture writ-
ing and vowed someday to translate it. Twenty years later Champollion
achieved his goal and became the first person in three thousand years to
read Egyptian hieroglyphics.

Champollion deciphered an ancient language which opened up Old
Egypt to modern scholarship. Fourier, the man who showed the stone to
Champollion, was also the discoverer of a new language, whose elements
are not hieroglyphs but wave forms. Fourier's theorem, the key to the new
wave language, is the foundation stone of all wave-based sciences includ-
ing communications theory, modern optics, sound reproduction, oceanog-
raphy, and quantum theory.

Fourier developed his waveform language to deal with heat waves. Heat
as the motive power behind the burgeoning industrial revolution was an
exciting mystery to nineteenth-century physicists and engineers. Lord
Kelvin, the dean of English physicists, described La Theorie analytique de
la chaleur, Fourier's elegant study of the flow of heat, as "a great mathe-
matical poem." Fourier's theorem states that any wave can be written as a
unique sum of sine waves.

The sine wave is a kind of undulatory archetype; its curvy profile is what
most people have in mind when they visualize a wave. Vibrating strings
and ripples in a pond are shaped each moment like sine waves. To see a
sine wave standing still, look sidewise at a stretched spring (or any other
helix).

Physicists like these waveforms because when they put a sine wave into
any linear system, a similar sine wave always comes out. Linear systems

change a sine wave's amplitude and phase but they never change its sinu-
soidal shape. Mathematicians like sine waves because no matter how many
times they differentiate them, the result is always more sine waves. After
listing the special attributes of this popular waveform, E. A. Guillemin
celebrated the sine wave in words unusually colorful for an electrical engi-
neer: "The sine wave is singled out as the one that shall forever be king
and ruler." One can almost hear the fanfare of trumpets.

Imagine a wave w stretched out in space. Wave w is not necessarily
oscillatory; it may take any shape whatever. Fourier's theorem says that
wave w may be written as a sum of sine waves with various spatial frequen-
cies k, amplitudes a, and phases p. Each word in Fourier's sine wave
language is a sine wave with a different value for k, a, and p. Translating a
wave into its sine wave words is called Fourier analysis. Wave w's Fourier
analysis looks schematically like this:

The particular sine waves which describe wave w are called its Fourier
spectrum, or sometimes its vibration recipe. Each vibration recipe is
unique: there is only one way to translate a wave into this sine wave
language. The gist of Fourier's important discovery is that sine waves form
a universal alphabet in terms of which any wave can be written.

Scientists have analyzed the sound waves produced by various musical
instruments in terms of Fourier's sine wave alphabet. Even when sounding
the same note, each instrument produces its own particular "tone color"
—a difference reflected in its vibration recipe. Each instrument leaves a
unique "Fourier fingerprint" in the air.

When we judge that a piano sounds different from a harpsichord, our
brain may be attending not to different wave shapes but to different
Fourier spectra. Physiological evidence (as well as our own experience)
suggests that the human ear is sensitive to the sine wave content of sound.
Coiled behind the eardrum, the cochlea, a tiny snail-shaped organ, turns
sound into electrical impulses—brain code for auditory sensations. Each
location along the cochlea's coil responds to a specific sine wave fre-
quency. This little snail in the ear acts like a biological Fourier analyzer.

Just as a wave can be broken up into sine waves, so the same wave can
be put together out of sine waves, an operation called "Fourier synthesis."
Fourier's theorem tells us how to build any imaginable wave out of sine
waves.

Music Synthesis

Until recently the sound of music was restricted to tonal qualities that
could be produced by instruments which actually exist. Now Fourier's
theorem provides the method and cheap transistor oscillators provide the
means for the creation of entirely new tone colors—sounds impossible to
produce by mechanical means. Composers of the New Music build sound
directly out of sine waves from the keyboards of electronic synthesizers.

An electronic music synthesizer is a collection of sine wave oscillators
whose amplitudes and frequencies can be varied in accord with custom-
ized vibration recipes. Each oscillator, vibrating at a selected amplitude,
produces sine waves that are brought together in a mixer to create the
desired tone color—either an imitation of an existing instrument or, more
likely, some entirely novel electronic sound.

Electronic instruments based on Fourier synthesis are called analog syn-
thesizers and were developed in the early sixties by New Music pioneers
Robert Moog, Donald Buchla, and Paul Ketoff. The more recent digital
synthesizers build their music not out of sine waves but out of waveforms
called impulse waves. An impulse wave is an infinitely narrow spike of
sound.

To picture digital analysis, imagine wave w going through a salami
slicer. This machine breaks up a wave into very thin waveforms (impulse
waves) which have the same amplitude as wave w at each location. As
each slice of wave falls away, record its amplitude as a number on a list.
These numbers are the wave's digital recipe or impulse spectrum. Plotting
these numbers on a graph gives a curve that looks exactly like the original
wave; the impulse spectrum of wave w is identical to the shape of wave w
in space.

Digital synthesis involves looking at a wave's digital recipe and produc-
ing a string of narrow pulses whose amplitudes match the numbers on the
list. Digital synthesis re-creates the salami by generating a sequence of
slices the same size as the original.

Moog (analog) synthesizers typically have dozens of sine wave oscilla-
tors which are few enough to be tuned by hand. Digital synthesizers need
to generate tens of thousands of "slices" to duplicate a sound lasting only
a fraction of a second. The only practical way to handle so many numbers
is in a computer memory. Analog synthesizers resemble a barbershop quar-

tet—a handful of voices singing in chorus; digital synthesizers are full-
fledged computers.

Newton's Prisms

Since 1822 when Fourier published his famous treatise on heat, sine wave
analysis has developed into one of science's most valuable tools with thou-
sands of practical applications. Recently Fourier techniques have prolifer-
ated due to development of computer programs which rapidly analyze
complex waveforms into their sine wave components.

Wave analysis is rather new, as scientific discoveries go. However, more
than a century before Fourier, Isaac Newton carried out a famous experi-
ment which foreshadowed the French savant's new language of waves. By
splitting sunlight with an upright prism into the familiar rainbow hues,
Newton showed that white light is composed of colors. Newton named
these colors "spectrum" from the Latin for "apparition." He also demon-
strated that these colors could be recombined into white light by means of
a second prism, inverted.

Borrowing from Newton, I symbolize any spectral analyzer—whether
sine wave or impulse wave—by an upright prism. A spectral analyzer splits
a wave up into component waveforms—sine waves in the case of a Fourier
analyzer. I represent a typical output waveform by two parallel lines: a
solid line standing for amplitude, a broken line representing phase, as a
reminder that waves carry both these attributes. Although non-oscillatory
waves have no cycles, time delay plays the role of phase for such waves. To
complete the picture, I represent a spectral synthesizer by an inverted
prism. Fig. 5.2 gives an example of this graphic convention.

The Synthesizer Theorem

Fourier synthesis builds waves with a sine wave alphabet; digital synthesis
creates the same waves out of impulse waveforms. If the same wave can be
synthesized two different ways, why not more? Mathematicians attempt-
ing to extend Fourier's theorem in new directions made a remarkable
discovery: almost any waveform family will work as the basic alphabet of a
wave language.

This discovery—which I call the synthesizer theorem—means that

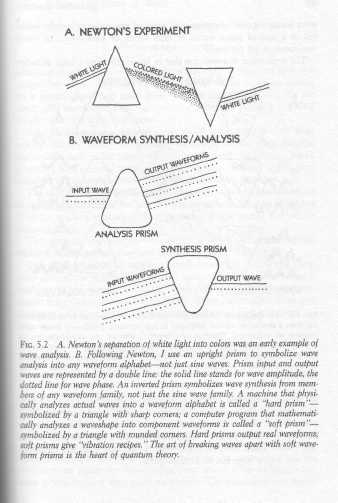
wave w can not only be expressed as a sum of sine waves or impulse waves
but as a sum of piano waves, or flute waves, or tuba waves, or weird
waveforms as yet unnamed.
The synthesizer theorem says that as far as providing a basic alphabet

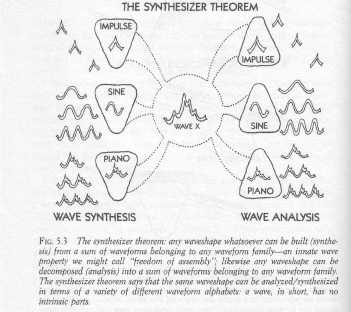
for waves is concerned, there's nothing special about Fourier's sine waves.
Any other waveform will do as well. By virtue of the synthesizer theorem a
particular wave can be decomposed many different ways—as many ways as
there are waveform families. This means that there is no "natural" way to
take a wave apart. Unlike a clock, which breaks into gears and springs in
just one way, a wave has no intrinsic parts.

Waveform Families

Members of a human family share some common features, yet each is a
unique individual. A member's family name tells what crowd he belongs
to; a member's personal name picks him out from that crowd. It's the
same with waveforms: each member of a waveform family has both a
family name and a personal name.

Take for instance the impulse wave family. Each impulse wave looks
exactly like any other—an infinitely narrow, spike-like wave. Impulse
waves differ only in the place where they're located. An impulse wave's
position x is its personal name, which distinguishes that wave from other
members of the impulse wave family residing at other locations.

The spatial sine wave family consists of regular oscillations stretched out
in space from horizon to horizon. All sine waves have the same shape but
differ in spatial frequency. Spatial frequency k is a spatial sine wave's
personal name.

The temporal sine wave family consists of regular vibrations in time
which are distinguished from one another by their frequency f.

The spherical harmonic waveform family consists of the natural vibra-
tions of a hollow sphere. The personal name of a spherical harmonic is
made up of two integers, n and m, which distinguish one spherical har-
monic from other members of its family. More information about this
illustrious waveform family may be found at the end of this chapter.

Kin Prism and Conjugate Prism

According to the synthesizer theorem, a wave w can be written in a
waveform alphabet drawn from an infinite number of waveform families.
However, for any particular wave there are two waveform families to
which it bears a special relationship. There is one family to which it is
closest in a certain sense, and one family from which it is most distant.

We analyze wave w into component waveforms by putting it through a
waveform family prism, which separates any input wave into pure wave-
forms belonging to the prism's family. As we analyze wave w with differ-
ent prisms we notice that some prisms break w into a few waveforms and
some prisms break w into many waveforms. The number of waveforms

into which a prism splits a wave is called that wave's spectral width, or
sometimes bandwidth.

The size of this bandwidth bears an inverse relation to how closely wave
w "resembles" the prism waveform which is analyzing it. The smaller the
bandwidth, the more wave w resembles the prism waveforms; the larger
the bandwidth, the less the family resemblance. For instance, if we put
wave w into its own family prism (call this the W family), it will be
analyzed into only one waveform, namely itself—the minimum possible
bandwidth. I call this prism—the prism that does not split wave w at all—
its kin prism. The waveforms associated with this prism are its own kind,
the family to which it belongs.

On the other hand, among all the waveform families in the world, there
is one family (family M) whose prism gives the largest possible bandwidth
when it's used to analyze wave w. The members of family M resemble w
the least. I call this prism—the prism that splits wave w the most—its
conjugate prism.

One can imagine every waveform family inhabiting a spherical wave-
space like the Earth's surface. Families which resemble the W family

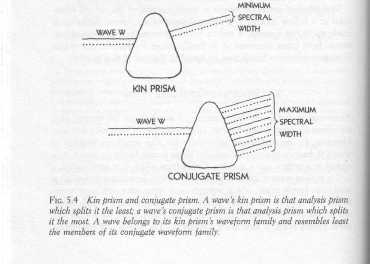
live nearby; families which are different from W live farther off. The
family most distant from W is its conjugate family M, which lives at the
antipodes—precisely on the other side of the world.

Just as every wave belongs to a unique waveform family, so every wave-
form family possesses a conjugate family whose members are its polar
opposites.

The sine wave family (the basis for analog music synthesis) consists of
smoothly oscillating waves without beginning or end. The sine wave's
conjugate waveform is the impulse wave (the basis for digital synthesis).
An impulse wave is a single narrow spike that lasts for an immeasurably
small instant. You could hardly imagine two waves more different than
these conjugate waveforms, sine wave and impulse wave.

one unit of spectral space. If you want to make a wave—no matter what
its shape—you will have to provide a certain minimum spectral acreage to
put it on. Since this rule resembles a kind of building code in spectral
space, I call it the spectral area code. An example of the spectral area code

Short percussive musical sounds, such as castanets, triangle, woodblock,
have a narrow impulse spectrum since their waveforms take up little space.
To analog-synthesize such crisp sounds adequately, the spectral area code
requires a large range of sine waves. To synthesize an infinitely short
sound, the impulse wave itself, would require all possible sine wave fre-
quencies.

On the other hand, musical sounds that are nearly pure tones, such as
flute, organ, tuning fork, have a narrow sine spectrum. To digitally synthe-
size such pure tones adequately, the spectral area code demands a large
range of impulse waves.

The spectral area code tells us that analog and digital music synthesizers
are complementary in a particular sense: one is good for synthesizing long
waveshapes, the other for short ones. The spectral area code is a basic
feature of all waves, as inseparable from their undulatory nature as diffrac-
tion and interference. This code is important in optics, where it limits the
resolving power of microscopes, in communications theory, where it fixes
the bandwidth of TV channels, and in numerous other wave-based opera-
tions. As we shall see, the spectral area code when applied to waves of
quantumstuff leads immediately to the Heisenberg uncertainty principle.

Although in its application to ordinary waves this code has been known
for more than a century, it never received a proper name. Now due to
semantic backformation more and more textbooks on ordinary wave the-
ory refer to this natural limitation on mutual spectral widths as the uncer-
tainty principle despite the fact that in its application to ordinary waves it
has nothing to do with uncertainty.

Whenever it is measured the world seems solid (particle-like), but the
pattern formed by these particles leads to the conclusion that between
measurements the world acts like a wave. Following this lead, quantum
theory represents the unmeasured world as a wave identical in its behavior
to ordinary waves, but interpreted in a decidedly non-ordinary manner.
This brief survey of basic wave behavior is intended to provide solid
ground from which we can venture into the slippery territory of quantum
interpretation.

Epilogue: A Family of Spherical Waves

Looking at droplets from a leaky faucet in the flickering glare of a strobe
light, you seem to see hanging in midair single quivering balls of water.
The oscillation of water droplets is conveniently described in terms of a
waveform family called the spherical harmonics.

Just as sine waves are the natural vibrations of a stretched string, so
spherical harmonics are the natural vibrations of an elastic sphere. If it is
shaped like a ball, chances are that some scientist has described it in the
spherical harmonic wave alphabet. Members of this waveform family por-
tray the figure of the Earth and its magnetic field, the radiation pattern
surrounding a TV antenna, oscillations of raindrops and atomic nuclei, the
heave of ocean tides, and the agitation of numerous spherical resonators,
from temple gongs to the sizzling surface of the sun.

Besides its family name, each spherical harmonic has two personal
names which distinguish that member's waveshape from the rest of the
family. Whenever a sphere vibrates, certain nodal circles appear where the
sphere stands still. On one side of the nodal circle, the sphere's surface is
moving in; on the other side of this boundary, the sphere is moving out.

A spherical harmonic's first name (commonly called its "order") is a
number n which counts its total number of nodal circles. The simplest
spherical harmonic has no nodal lines at all (n = 0): the entire sphere
expands and contracts as a whole, a style of spherical motion called the
"breathing mode." Each spherical harmonic possesses an axis of symmetry
marked like the axis of the Earth by north and south poles. A spherical
harmonic's second name (commonly called its "degree") is a number m
which counts how many of its nodal circles pass through its poles. A
general property of spherical vibration is that if a nodal circle doesn't go
through the poles, then it must lie in a plane parallel to the sphere's
equator. Consequently all nodal circles are lines of definite latitude or
longitude.

For instance the spherical harmonic labeled n = 5, m = 4 (fifth order,
fourth degree) has five nodal circles in all, four of which pass through its
poles. The odd nodal circle must be a line of latitude which, for reasons of
symmetry, passes through the equator. For the spherical harmonic wave-
form family, two numbers suffice to list all family members. Nobody is left
out.

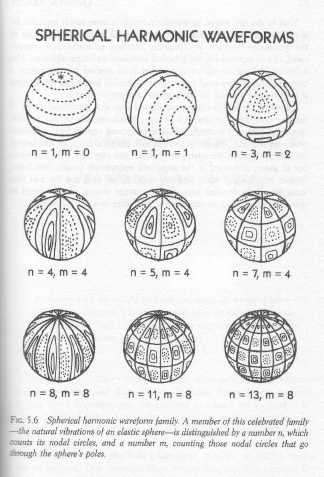
Next to the sine waves, no waveform family is more highly regarded by
scientists working with waves than the spherical harmonics. By virtue of
the synthesizer theorem, any spherical vibration, no matter how compli-
cated, can be expressed in the spherical harmonic waveform alphabet. The
behavior of these useful waveforms has been studied for more than a
century. That the personal names of the spherical harmonics are integers
is of particular interest for the purpose of quantum theory.

All waveform families so far considered possess a continuous range of
names—quantities like spatial frequency, which can take on any possible
numerical value. In contrast, spherical harmonics possess personal names
which are discrete. Waveform families with discrete names are like fretted
instruments (guitar, trumpet, piano) which can play only a limited num-
ber of notes, compared to the unfretted instruments (violin, trombone,
human voice) which can sound any note. As we shall see, the fact that
some waveform families have discrete names means, when applied to
quantum waves, that certain physical attributes must be quantized.

6 - Meet the Champ:
Quantum Theory Itself

"By nature I am peacefully inclined and reject all doubtful adven-
tures. But a theoretical interpretation had to be found at all costs,
no matter how high ... I was ready to sacrifice every one of my
previous convictions about physical laws."

---Max Planck

A visitor to Niels Bohr's country cottage asked him about a horseshoe
nailed above the front door. "Surely, Professor Bohr, you do not really
believe that a horseshoe over the entrance to a home brings good luck?"
"No," answered Bohr, "I certainly do not believe in this superstition. But
you know," he added, "they say it brings luck even if you don't believe in
it."

Quantum theory is like Bohr's horseshoe: it works no matter what a
person believes. One quantum theorist may imagine she's charting the
destinies of multiple worlds; another fancies he's thinking quantum logi-
cally. Despite different notions about what they're doing (indicative of

physicists' confusion about what quantum theory actually means), both
theorists will come up with the same result.

Quantum theory was devised in the late twenties to deal with the atom,
a tiny entity a thousand times smaller than the wavelength of green light.
Disturbed by its philosophical implications, many physicists at that time
considered quantum theory a provisional device bound to fail outside the
atomic realm. Quantum theory continued, however, to prosper beyond its
inventors' wildest dreams, resolving subtle problems of atomic structure,
tackling the nucleus some ten thousand times smaller than the atom itself,
and then extending its reach to the realm of elementary particles (quarks,
gluons, leptons) which many believe to be the world's ultimate constitu-
ents. With each success quantum theory became more audacious. Quan-
tum physicists looking for new worlds to conquer turned their sights to the
macrocosm, and now dare to model the birth of the universe itself as one
gigantic quantum jump. Heaping success upon success, quantum theory
boldly exposes itself to potential falsification on a thousand different
fronts. Its record is impressive: quantum theory passes every test we can
devise. After sixty years of play, this theory is still batting a thousand.

Before looking at the quantum reality question, which sharply divides
them, let's begin where physicists all agree: how to actually use quantum
theory. From Berkeley to Gorky, quantum physicists predict quantum
facts in exactly the same way. In this chapter I treat quantum theory
strictly as a tool for predicting experimental results, and do not inquire at
all as to what it might mean.

Considered merely as a tool, quantum theory is a conceptual recipe
which predicts for any quantum entity which values of its physical attri-
butes will be observed in a particular measurement situation. Quantum
theory by design only predicts the results of measurements; it does not tell
us what goes on in between measurements.

Quantum theory predicts the results of measurement with unsurpassed
accuracy, but measurements are only part of the world. Most everywhere,
most of the time, the world dwells in an unmeasured state. Anyone curi-
ous about reality will want to know what the world is like when it is not
being measured. Quantum theory does not directly address this question.

We can get a sense of how quantum theory operates by answering three
questions:

1.  How does quantum theory describe a quantum entity?

2.  How does quantum theory describe a physical attribute?

3.  How does quantum theory describe a measurement situation?

Once we understand how physicists actually use quantum theory to pre-
dict a quantum entity's measured attributes, we will look at some attempts
to go beyond quantum theory to the unmeasured world itself.

kitchen sink. Interference of quantum waves, however, gives peculiar re-
sults. Because quantum possibilities add like waves, not like things, physi-
cal possibilities can vanish if their representative waves happen to meet
out of phase.

Not long ago a simple case of interfering possibilities changed the
course of elementary-particle physics. In the late sixties physicists had
good reason to believe that all strongly interacting particles (hadrons) were
actually composed of a few truly fundamental particles called quarks. At
that time, combinations of only three quarks—distinguished by a "flavor"
quantum number as up, down, or strange—sufficed to account for the
existence of dozens of known hadrons.

In 1970 Harvard physicist Sheldon Glashow conjectured that a fourth
(charm-flavored) quark must exist and he estimated both the properties of
the charmed quark and new yet-to-be-discovered hadrons that could be
built from it. One of Glashow's best arguments for the charmed quark's
existence was the nonexistence of a particular decay mode of the K-par-
ticle. Like most of its sister hadrons, the K-particle is unstable and decays
in numerous ways into less massive particles. Yet despite long searches, the
K-particle had never been observed to decay into two muons.

According to the three-quark model of hadrons, the K-particle's quark
structure demanded that it decay into a pair of muons in a certain way—
via the strange quark channel. (The up and down quarks can't make
muons.) Yet this decay mode never seemed to occur. Would physicists
have to scrap the quark model because it predicted a process that didn't
happen?

Glashow's plan for eliminating two-muon decay was not to do away
with quarks but to add one more. He postulated a second way that the
K-particle could change into two muons, a way which involved a new
quark—the charmed quark channel. In classical physics, if you double the
number of ways something can happen, you expect that it will happen
twice as often. Not so in quantum physics, which permits the cancellation
of possibilities. Glashow tailored the properties of the new quark so that
its possibility wave was opposite in phase from the strange quark's wave.
The two possibilities cancel, nicely suppressing two-muon decay. Actually,
because these quarks have different masses the cancellation is not quite
exact. Recent measurements of K-particle decay have uncovered a few
double-muon events, less by a factor of a million from the three-quark
predictions but in line with Glashow's four-quark model. So convinced
was Glashow that the absence of muons signaled the presence of charm,

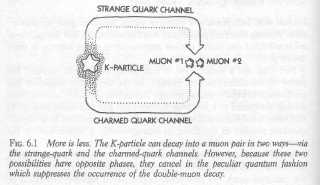
that at the Fourth International Conference on Meson Spectroscopy
(April 1974) he promised to eat his hat at their next meeting two years
hence if charm was not discovered in the meantime.

Glashow did not have to eat his hat. In November 1974 the J-particle
was discovered, the first of the new charm-constituted hadrons. Subse-
quently other charmed particles showed up. Today quark theory is a cor-
nerstone of particle physics. Theorists see a need for two more quark
flavors (top and bottom), making six flavors in all. Confidence in the
existence of quarks is now so high that, unlike the suspense attending
Glashow's bold conjecture, confirmation of top and bottom quarks is re-
garded as almost inevitable.

This destructive interference of a quark's physical attribute (its ability
to decay into muons) represents a routine application of quantum con-
cepts at the frontiers of present knowledge. This example reinforces our
belief that quantum theory applies to all physical entities without excep-
tion. No entity is so exotic that it escapes the quantum rules: a quark's a
quon too. One description fits all.

The answer to our first question—How does quantum theory describe a
quantum entity?—is this: quantum theory does not "describe" entities at
all; it represents them. Instead of dealing directly with a quantum entity,
quantum theory replaces it with a proxy wave [psi], whose square at any
location gives the probability that the quon's particle aspect will manifest

ere (position attribute) and whose shape gives information about all
tributes other than position, in a manner to be described next.

crete. The position attribute is associated with the impulse wave family of
waveforms. Each impulse wave represents a different value of position. A
typical member of this family is an extremely tall, infinitely narrow pulse
located exactly at position x. The position value X associated with this
family member is the same position x at which this waveform is located: X = x

The momentum attribute is associated with the spatial sine wave family
of waveforms. Each sine wave represents a different value of momentum.
A typical member of this family resembles an infinitely long oscillation
stretching into the distance with spatial frequency k. The momentum
value P associated with each family member is given by the relation:

P=hk

where h is Planck's constant of action.

The energy attribute is associated with the temporal sine wave family of
waveforms. Each sine wave represents a different value of energy. A typi-
cal member of this family is a pure musical note vibrating at frequency f.
The energy value E associated with each family member is given by the
relation: E = hf

where h is again Planck's constant.

The spin attribute is associated with the spherical harmonic family of
waveforms. Each spherical harmonic represents a different value of spin
magnitude and spin orientation. A typical spherical harmonic looks like a
globe of quivering jelly whose regions of vibration are partitioned by a
certain number n of nodal circles, a number m of which pass through the
poles of the sphere. The spin magnitude S is given by the total number of
nodes n according to the rule: S = hn

Because n and m count nodal circles, they are restricted to integer values.
This means that both spin magnitude and spin orientation can take only
certain discrete values. Such attributes are said to be "quantized."

Classical physics placed no limits on the values an object's spin could
take: Newton's apple could spin any way it pleased. Quantum theory, on
the other hand, requires spin and other special attributes to be quantized
—they can take only certain values and not others. Quantized attributes
are digitized: they can be measured with perfect accuracy, a quantum fact
which compensates somewhat for the fundamental quantum inaccuracy
required by Heisenberg's uncertainty principle.

Quantum theory's waveform-attribute connection explains why some
attributes are quantized and others are not. Quantized attributes corre-
spond to confined waveforms like the spherical harmonics, whose vibra-
tions are restricted to the surface of a sphere.

An unconfined wave—a sine or impulse wave, for instance—vibrates as
it pleases; a confined wave vibrates only at certain resonant frequencies.
This constraint on vibratory states translates into a constraint on numbers
of waveform family members that explains why not all values of certain
attributes can occur in nature.

Quantum theory's association of attributes with waveforms can be ex-
pressed as a quantum waveform-attribute dictionary listing for every dy-
namic attribute its corresponding waveform family. A portion of this
quantum dictionary is shown in Fig. 6.2. Along with each waveform-
attribute entry in the quantum dictionary goes a rule for translating a
waveform's personal name into the size of its corresponding attribute.
This rule usually (but not always) involves Planck's constant.

Here is a list of some of these rules:

these historic equations as simple consequences of the waveform-attribute
connection. But these two rules are just the tip of the quantum iceberg:
for every dynamic attribute there is such a formula which connects the
size of some mechanical attribute with a particular wave property: the
personal name of its corresponding waveform.

The waveform-attribute connection is without a doubt one of quantum
theory's most unusual features. It seems natural to associate a wave with
each quon since quons show some wavelike aspects. But how can we
justify the association of abstract waveforms with mechanical attributes?
What on earth does momentum have to do with sine waves?

Ultimately this waveform-attribute association is justified because it
works. A realist would say that it works because it reflects some correspon-
dence really present in the world: nature has associated momentum with
sine waves from the beginning. Humans have only recently discovered the
naturalness of this connection. For thousands of years our culture has been
shaped by literature, liturgy and legislation built of human language. In
The Cosmic Code Heinz Pagels pictures the scientific enterprise as the
opening of the "Great Book of Nature": the discovery and decoding of
the ancient non-human message which orders the universe. The cosmic
code entered our awareness only yesterday, but already the strange beauty
of this alien language is restructuring human culture to its own design.

The biology sector of the cosmic code is dominated by the DNA code,
which associates certain molecular trigrams with particular amino acids—
the building blocks of life on Earth. The key to the cosmic code's quan-
tum sector is a code that assigns a particular waveform to every physical
attribute. The quantum waveform-attribute code is more general than
DNA: sinewave means momentum for quons all over the universe.

According to quantum theory any waveform, no matter how bizarre,
corresponds to some particular dynamic attribute which we could in prin-
ciple measure. There is an infinity of possible waveform families, which
means that the waveform-attribute dictionary contains an infinite number
of entries.

For instance the "piano" waveform connects to some presently un-
known mechanical attribute—call it the piano attribute—which an elec-
tron or any other quon is bound to display in a piano measurement situa-
tion. Likewise we could test an electron for the size of its tuba attribute,
its flute attribute, or its Wurlitzer organ attribute. Physicists have shown
little interest in measuring such obscure mechanical properties, but should

like Maxine's prisms but an actual material object. The A-analyzer is a
machine that works like this: you put in a beam of quons (each repre-
sented by the same wave function) and the A-analyzer sorts them into two
beamlets, one whose quons all have A value A1, and the other whose
quons have A value A2. In each of these beamlets sits a detector (which
could be a phosphor screen) which counts and records the number of
quons in each channel. To measure any attribute, simply count how many
quons display each value of that attribute.

Quantum theory, in this case, predicts that 75 percent of the electrons
will show value Al and the remaining 25 percent will end up in the A2
detector. In every case where probabilities like these have actually been
compared with experiment, the facts have agreed with theory. Had this
been an actual test, with any quon beam, with any attribute, no physicist
would wager against quantum theory. In millions of experimental situa-
tions, in hundreds of different laboratories, this unusual predictive proce-
dure has never missed the mark. In the lab, an experimentalist deploys an
actual quon beam, an actual attribute sorter which separates these quons
into beamlets with different attribute values, plus actual detectors which
count the number of quons in each beamlet.

On paper, a theorist replaces the quon beam with a fictitious proxy
wave and replaces the attribute sorter with a soft waveform analyzer,
which breaks the quon's proxy wave into a spectrum of fictitious wave-
forms which take the place of attributes in this theory. The intensity
(amplitude squared) of each output waveform predicts the probability that
its corresponding attribute will appear in the experimental attribute spec-
trum.

Quantum theory parallels the actual measurement of a quon's physical
attributes with a mathematical charade starring a fictitious proxy wave and
its constituent waveforms. This wholly wavelike representation is recon-
ciled with the fact that every actual quantum event is (like the flash on a
phosphor screen) wholly particle-like by construing these quantum waves
to mean not the events themselves but the pattern of these events. Be-
cause they correspond to patterns of particles, these quantum proxy waves
behave less like ocean waves, more like "crime waves"—the kind of wave
that governs the shape of the forest rather than the location of individual
trees.

In practice quantum theory cannot be distinguished from classical the-
ory in many situations (quantum gravity, for instance) because the new

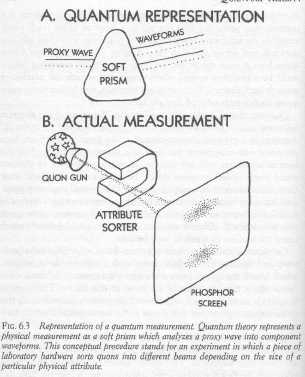
effects it predicts are too tiny to measure. In addition the scope of both
quantum experiment and theory is limited by the experimental and com-
putational means of present-day technology. One of these technical limita-
tions is the difficulty of computing the waveforms which correspond to
certain attributes. Theorists can easily calculate the waveform-attribute
connection for attributes of elementary quons, but these calculations rap-
idly become more difficult as the quons get more complex. The calculation
of the attributes of molecules is not easy; to compute the waveform which

corresponds to the heads/tails attribute of a flipped penny is beyond the
reach of today's mathematics.

On the experimental side, it's easy to measure flipped pennies, but
often very difficult (and expensive) to construct for elementary quons the
attribute sorters we so casually invoke on paper. On the other hand, for an
elementary quon's major attributes, physicists have been able to devise
such sorters.

The position attribute can be measured with a phosphor screen or with
several other detectors sensitive to a quon's raw presence. Your eye is a
position-attribute sorter of photons.

For charged particles a uniform magnetic field acts as a momentum
sorter, and for neutral particles a non-uniform magnetic field can sort
quons according to their spin magnitudes and orientations. As we shall
see, certain transparent crystals can sort photons according to their polar-
ization attribute, an attribute of light closely related to the photon's spin.

Some attribute sorters cost millions of dollars—the machine, for exam-
ple, which counts how many K-particles possess the two-muon decay attri-
bute; other sorters are extremely simple. The Airy experiment (Fig. 4.1) is
an example of a momentum sorter consisting of nothing but a small hole
and a phosphor screen. Any quon which passes through the hole with zero
sidewise momentum strikes the center of the screen. The more (sidewise)
momentum a quon has, the more it will drift sidewise in transit and hit
the screen off center. The Airy pattern, in addition to demonstrating the
wave nature of electrons, also records the (sidewise) momentum spectrum
of these elementary quons.

gal relations look like "uncertainties." From the inside—the quon's point
of view—they feel like "realms of possibility," the basic inalienable estate
of every quon in the universe.

Quantum theory represents each quon by a proxy wave, and its mechan-
ical attributes by specific waveforms. The proportion of an attribute's
waveform which the wave function displays when analyzed with respect to
that waveform-attribute family represents the probability of measuring an
attribute with that value. This theory deals with the world in a particularly

indirect manner. It focuses strictly on measurement acts, not on how the
world might behave between measurements; it does not describe single
measurement events but only patterns of events, for which it gives merely
statistical predictions.

Reality researchers want more. They want to know what the single
events which make up the world are doing both between and during
measurements. Quantum theory predicts the facts perfectly, but it leaves
us in the dark concerning this other kind of reality. Einstein expressed this
desire to look behind the facts when he said, "I still believe in the possibil-
ity of a model of reality, that is to say, of a theory, which represents things
themselves and not merely the probability of their occurrence."

In the next chapter we look at some attempts to go beyond quantum
theory to the things themselves.

7 - Describing

The Indescribable:

The Quantum Interpretation

Question

"They are not smooth-surfaced, rectangular or carbon-ringed units
which fit together like bricks. Each molecule is a heavenly octopus
with a million floating jeweled tentacles hungry to merge."

---Timothy Leary

Quantum facts such as the one-hole diffraction experiment suggest that
each electron acts like a wave between observations, but behaves like a
particle whenever it is observed. Quantum theory—the math that de-
scribes these facts—likewise reflects each quon's double identity by repre-
senting an unmeasured entity by a particular waveshape—whose form
encodes the probability of observing a particle-like event with definite
location and attributes. Both quantum theory and quantum fact support
the notion that the real situation of an unmeasured electron (or any other
quon) is radically different from the reality status of any electron anyone
has ever measured.

Some physicists would like to blame the quantum dilemma on the
observer's inevitable disturbance of what he measures. However, if we take

quantum theory seriously as a picture of what's really going on, each
measurement does more than disturb: it profoundly reshapes the very
fabric of reality.

We might imagine, as a model of a disturbing measurement, trying to
locate accurately a swiftly moving wasp that wants to escape our caliper's
jaws: the quantum world—delicate and dynamic—is just too skittish for
our clumsy instruments to pin down.

Simple disturbance models of this kind, however, fail to do justice to
the quantum description. Quantum theory suggests that before we mea-
sure the particle (wasp), it's not a particle at all but something as big as a
whale (wave). Calling quon measured a wasp, unmeasured quon a whale
still misses the flavor of a quantum measurement because wasp and whale
are still both animals. In the quantum description an unmeasured quon
does not enjoy the same style of existence as a measured quon; an unmea-
sured quon dwells in a more attenuated state of reality than the quons
which appear on our phosphor screens.

Imagine that the whale dwells not in the real world but on the spirit
plane; the wasp is real. Now we are closer to the sense of the quantum
description. Whenever a measurement occurs anywhere in the world,
something like a ghostly whale (immense, insubstantial, permeable, and
wavelike) turns into something like a real wasp (minute, substantial, and
particle-like). A quantum measurement resembles good stage magic more
than a clumsy meter reading.

In terms of the whale/wasp analogy, the quantum reality question di-
vides into two parts: 1. what is the nature of the whale? 2. how does the
whale change into a wasp? The quest to describe the whale is called the
"quantum interpretation question." This mystery beast—a quon in its
wild, unmeasured state—is represented by a wave function. The interpre-
tation question asks: what does the quon's proxy wave tell us about the
factual situation of an unmeasured quon?

The matter of how whale becomes wasp is called the quantum measure-
ment problem: what does the quantum representation of a measurement
—as a soft prism splitting a proxy wave into waveforms—tell us about
what actually goes on in the measurement act?

I discuss the quantum measurement problem in the next chapter, and
consider here the quantum interpretation question. What is the nature of
quon unmeasured? Can we describe the world's unseen whales in words or
must we remain silent? In between observations a quon is represented by

its proxy wave: the wave function is the best clue we have concerning the
real nature of the unmeasured universe.

When dealing with a new quantum entity, a theorist's main problem is
how to construct its wave function. She commonly resorts to solving some
sort of wave equation, such as Schrodinger's equation for slow quons, or
Dirac's equation for quons moving near the speed of light.

Feynman's Sum-over-histories Version of Quantum Theory

In 1948 Richard Feynman, then at Cornell, devised a way of computing a
quon's wave function so unusual that it ranks as a quantum-theoretical
fourth way, comparable to Heisenberg's matrix mechanics, Schrodinger's
wave mechanics, and Dirac's transformation theory. Feynman's method,
called the sum-over-histories approach, is useful not only for computations
but for the insight it gives into what the wave function might mean.

Feynman was inspired by the work of Christian Huygens, a seven-
teenth-century Dutch physicist who invented a new way of analyzing light
waves by breaking them up into simple sums of spherical wavelets. In the
twentieth century Richard Feynman adapted Huygens' technique to
quantum waves by breaking them up into simple sums of "elementary
histories." As an illustration of his method, let's look at how Feynman
might go about constructing the quantum wave for the one-hole diffrac-
tion (Airy pattern) experiment. Fig. 7.1 shows the familiar quon gun
snooting electrons at a phosphor screen through a circular hole. To calcu-
late the electron's proxy wave [psi], Feynman postulates that the wave ampli-
tude on the screen is equal to the sum of the amplitudes of all possible
ways that an electron can get there from the quon gun. Furthermore all
paths are equally important, none better than any other. Feynman imple-
ments this quantum democracy of possibilities in his scheme by assigning
the same amplitude to every path. Each path differs from its fellows only
by its phase. A path's phase at any location depends on its history, the
route that brought it there.

Feynman assumes that the unmeasured world works according to two
rules:

1.  A single quon takes all possible paths.

2.  No path is better than any other.

These rules do not mean that an unmeasured electron is free to take any
path it pleases. The electron has no choice: if it follows the Feynman
rules, the electron is bound to take all paths at once. Furthermore, the
quantum democracy of possibilities forbids a quon from "treading harder"
on one path and skipping lightly over others. Even though we usually
observe an electron near its classical path, that path is no more special in
Feynman's scheme than a "wild" path that zigzags crazily toward the
screen.

Feynman's idea of getting probabilities by adding up possible paths has
much in common with classical statistical reasoning. Gamblers, for in-
stance, compute dice odds by counting how many "dice paths" add up to
seven, and so on—the more dice paths there are, the more probable the
outcome.

Electrons are odder than dice because: 1. a single electron takes all
paths—a single die takes one; 2. electrons have phases and dice don't. If
dice (unobserved) took all paths and were equipped with phases, one could
imagine a situation where you could throw a six with each die by itself but

could never throw boxcars (double sixes) because sixes have opposite
phases and cancel each other out.

But if the electron sprawls out across space, going everywhere at once,
why does it seem in your TV tube to travel in a straight line? Fig. 7.1
shows three Feynman paths for an electron, two more or less straight
paths near the classical trajectory, and one "wild" path.

In the process of adding up his paths, Feynman discovered that next to
every wild path runs a parallel path with exactly opposite phase. Since two
waves with equal amplitude and opposite phase totally cancel, complete
destructive interference removes all wild paths. Only in the vicinity of the
classical electron trajectory—in this case the straight line connecting gun,
hole, and screen's center—do any paths survive. Because paths add in
phase near the classical path, the wave function's amplitude is largest
there. Ironically the fact that an electron has phase—a typically quantum
property—is what saves the day for classical physics: if electron paths
couldn't interfere, the electron would be zipping all over the place.

Feynman's method works: summing up all paths gives the same wave
function as solving Schrodinger's equation. For the one-hole diffraction
experiment, the sum-over-histories approach yields the familiar Airy pat-
tern centered around the classical straight-line electron trajectory.

Feynman's discovery that he could build a quon's wave function by
summing over its possible paths gives us a better view of the wave func-
tion's nature than does merely solving an equation. The sum-over-histories
approach suggests that the quantum proxy wave represents the totality of
possibilities—plus mutual phases—open to a quantum entity. My use of
the term "possibility wave" for a quon's wave function and "realm of
possibility" for a quon's "uncertainty" is motivated by Richard Feynman's
picturesque approach to quantum theory.

The Orthodox Ontology

Speculation about what actually goes on in the world between measure-
ments goes against the prevailing fashion in physics. Most physicists use
quantum theory as a tool for calculating results and "leave it to the philos-
ophers" to wonder what's really going on behind the mathematics. Al-
though physicists officially plead ignorance concerning the ontological
status of unmeasured quons, they in fact adhere to an unofficial party line

which I call the orthodox ontology. Most physicists accept this ontology
without question; only a few mavericks do not.

The orthodox ontology rests on one simple postulate concerning the
real physical situation of an unmeasured quon. This postulate cannot be
verified experimentally, nor can it be derived logically. It is difficult to say
exactly where this postulate comes from, except that it represents most
physicists' intuitive feelings about how the quantum world actually works;
it summarizes a sense of the very nature of things acquired over years of
contact with the details of quantum theory and how it is applied in prac-
tice. This postulate may not correspond at all to the reality underneath,
but if it doesn't the majority of physicists will have to change their tune.

The central postulate of the orthodox ontology is this: All quons repre-
sented by the same proxy wave are physically identical. Two quons repre-
sented by the same proxy wave are said to be "in the same state." In terms
of quantum states, this postulate reads: "All quons in the same state are
exactly alike."

For example, every electron that goes through the hole in the Airy
experiment is described by the same proxy wave: all Airy electrons are in
the same quantum state. According to the orthodox ontology, before
they're measured the physical situation of each of these electrons is abso-
lutely identical: there is no difference whatsoever between electron #123
and electron #137.

Physicists use the wave function to calculate the probability that certain
attribute values will be realized upon measurement. Because it deals in
probability, the wave function—like dice odds—has an obvious statistical
meaning which is relevant to the behavior of a large number of quons. But
because of the orthodox identity postulate, the wave function describes a
single quon as well. If all quons are physically identical, the distinction
between a statistical description and an individual description vanishes.

In the Airy experiment, all electrons do not strike the same phosphor
molecule but hit different spots on the screen. If all electrons are really
alike, why do they behave differently? The orthodox ontology explains the
fact that unmeasured electrons are identical in being but different in be-
havior by appealing to quantum randomness. The essence of quantum
randomness is simply this: identical physical situations give rise to differ-
ent outcomes.

Once you get down to the quantum randomness level, no further expla-
nation is possible. You can't go any deeper because physics stops here.
Albert Einstein, no fan of the orthodox ontology, objected to this funda-

mental lawlessness at the heart of nature when he said that he could not
believe that God would play dice with the universe. This new kind of
ultimate indeterminism may be called quantum ignorance: we don't know
why an electron strikes a particular phosphor because there's nothing
there to know about. When the dice fall from the cup, on the other hand,
their unpredictable outcome is caused by classical ignorance—by our un-
avoidably partial knowledge of their real situation.

Because they believe in the orthodox ontology, Bohr and Heisenberg
can claim that despite its statistical character, quantum theory gives a
complete account of the facts. Critics who object that this theory does not
explain the observably different outcomes of electrons in the same state
fail to appreciate the nature of quantum randomness: identical situations
give different results. That's all there is to it. If the orthodox ontology is a
true vision of things, there's absolutely nothing in the unmeasured elec-
tron's physical situation that tells where it's going to strike the screen. To
demand that quantum theory give such information or be judged "incom-
plete" is to ask for the impossible. Quantum theory gives the most com-
plete description of the electron's state of affairs consistent with the elec-
tron's real nature. To add more would be, as the Chinese say, "to put legs
on the snake."

Thus when we see a flash in the Airy experiment we should not imagine
that just before the event, a tiny electron was heading for one particular
phosphor molecule. According to the orthodox ontology, before a mea-
surement occurs, all of an unmeasured electron's possibilities are live pos-
oilities: just before it strikes the screen, the electron is not headed in a
particular direction. If we must talk about it at all, just before it hits, the
electron is headed everywhere at once. The rule of the road for unmea-
sured electrons is this: a single quon takes all paths.

Summing up the orthodox ontology:

1. All quons in the same quantum state are physically identical.

2. The wave function gives a complete account of the physical situation

of a single quon.

3. The relationship of the experimenter to an unmeasured quon is one of

quantum ignorance: the knowledge he lacks is simply not there to be

known.

4. A single unmeasured quon takes all paths open to it.
5. Measured differences between identical unmeasured quons arise from

quantum randomness.

The Orthodox Ontology's Opposition

Although most physicists accept the orthodox ontology, a small but presti-
gious minority believe that the world works along different lines. Distin-
guished dissidents from the quantum identity doctrine include Albert Ein-
stein, Louis de Broglie, Erwin Schrodinger, David Bohm, and John
Stewart Bell, as well as many lesser lights. These physicists offer various
alternatives to orthodox reality, but most of their proposals involve ex-
plaining the world in terms of familiar classical concepts, a quantum real-
ity I've termed neorealism.

Opponents of the orthodox ontology deny its primary postulate and end
up with a diametrically opposite view of unmeasured reality which looks
like this:

1.  Quons in the same state are physically different.

2.  The wave function gives a statistical description of an ensemble of
quons, and a necessarily incomplete description of a single quon.

3.  The experimenter's relationship to an unmeasured quon is one of classi-
cal ignorance: certain variables which quantum theory omits are hidden
from view.

4.  A single unmeasured quon takes one (usually unpredictable) path.

5.  Quons in the same state show measurable differences because they
were physically different before measurement.

Because of their belief that quantum randomness stems not from utter
lawlessness but from hidden causes, these heretics from the orthodox view
are sometimes called "hidden-variable" physicists. Their goal is to "com-
plete" quantum theory by constructing a deeper theory which includes an
explanation not only of its randomness but of what actually goes on in a
measurement.

In a typical hidden-variable model of reality, the world is described in
the same manner whether observed or not. The electron in particular is
always a particle, just as it seems to be whenever we look at it. However,
the electron's motion is controlled by an invisible force field—the so-
called pilot wave—whose properties are adjusted to reproduce the experi-
mental facts. In this model of reality, the world is made of both particles
and waves, not a single substance that shows both aspects.

Hidden-variable models were originally invented to "complete" quan-

turn theory by accounting for its otherwise inexplicable random results. As
a philosophical bonus, such models also describe reality without sancti-
fying the measurement act, restoring a refreshing sense of objectivity to
physics. In the hidden-variable version of reality, measurements are ordi-
nary interactions no different from nature's other interactions. Hidden-
variable realities are also entirely picturable in classical terms: there are, for
instance, no ghostly white whales swimming around between measure-
ments. Hidden-variable models are philosophically attractive, but they
possess one serious drawback which diminishes their value in the eyes of
most physicists.

In the orthodox view the world is represented by a fictitious proxy wave
with no pretentions to being real. On the other hand, in the hidden-
variable models, the wave that tells the electron how to move is considered
just as real as the water in the Pacific Ocean or the field surrounding a bar
magnet. In order to match the quantum facts, this real wave must possess
some quite remarkable properties: primarily it must connect with every
particle in the universe, be entirely invisible, and travel faster than light.

Gravity likewise connects every particle in the universe. Physicists are
not particularly bothered by this aspect of the pilot wave. The fact that
the pilot wave is in principle unobservable (you can only infer its presence
from its effect on the electron) disturbs physicists a bit because of the high
value they place on observability. However, the fact that the quark may
also be unobservable in principle (in most models of elementary particles a
quark combines with other quarks too strongly ever to be isolated) has not
diminished physicists' enthusiasm for these hypothetical entities. A more
serious objection than invisibility is that in these hidden-variable models,
an electron's pilot wave routinely travels faster than light.

Most physicists simply refuse to imagine that each electron in the world
is guided by an invisible superluminal wave. Bell's theorem shows that all
efforts to eliminate the superluminal character of these waves must fail.
Bell proves (among other things) that it is impossible to construct a hid-
den-variable model which explains the facts without including something
that goes faster than light.

We acknowledge for the moment the neorealist point of view but will
continue to explore visions of reality consistent with the orthodox ontol-
ogy.

Indeed, we already know what it would be like to live inside an atomic
wave function, because we walk around "inside atoms" whenever we go
outdoors on a starry night.

Starlight Proxy Waves

The size of an atom is equal to its realm of spatial possibilities—no more
than a few billionths of an inch. Excited atoms may puff up to more than
a thousand times this size, still too small to see. On the other hand, the
spatial realm of a single photon from a distant star can vary from a few
feet in diameter to an area the size of Texas.

The spatial realm of each star's photons depends inversely on that star's
apparent angular size. Small faraway stars have an enormous realm; the
realms of big nearby stars are smaller. The smallest realm in the sky
belongs to Betelgeuse, a giant red star in Orion's shoulder, whose realm on
Earth is approximately ten feet in diameter. This means that the proxy
wave of each photon from Betelgeuse is bigger than a bathtub.

The Heisenberg uncertainty principle explains the large spatial realms
of starlight. Imagine a beam of photons leaving Betelgeuse (520 light-years
away) heading in Earth's direction. Unless these photons possess ex-
tremely small sidewise motion, they will drift out of the beam during their
500-year transit time. To travel from a distant star and strike a target as
small as your open eye, a beam of starlight must possess a very tiny spread
in sidewise momentum. According to Heisenberg's principle, a small
spread in (sidewise) momentum requires a compensatory large spread in
(sidewise) position. That's why the photons from Betelgeuse are ten feet
wide. Other stars have wider wave functions.

How thick are these photon proxy waves from the stars? Applying the
uncertainty principle in the photon's direction of motion, we calculate a
realm of positional possibility thinner than a soap bubble. These stellar
proxy waves have the look of very wide, bubble-thin pancakes hurtling
through the night sky at the speed of light.

Living inside a photon's proxy wave we notice nothing unusual. In
particular, a photon detector (your eye, for instance) exposed to light from
Betelgeuse does not see a thin ten-foot-wide luminous disk. All that's ever
seen by eye or phosphor screen is an occasional flash of light. Every direct
measurement of light reveals it to be a point particle—the measured pho-

ton, like the measured electron, always seems to have zero radius. If we
could crawl inside a hydrogen atom, I'm sure we'd see the same thing.
Individual electrons, like individual photons, always appear as particles to
our instruments, even in cases where their wave functions are bigger than
the apparatus which measures them.

Despite the fact that our detectors never report anything but pointlike
particles, physicists have figured out how to measure the size of these
stellar proxy waves.

Deep in the Australian Outback, three hundred miles northwest of
Sydney in the village of Narrabri, British physicist Robert Hanbury Brown
built the world's first stellar intensity interferometer. He completed this
instrument in 1965 and used it to determine the angular diameter of stars
by measuring the widths of their photon proxy waves.

The apparent angular diameter of a star measures how much space it
takes up in the sky. The sun and moon, for instance, each take up about
half a degree of skyspace. (The width of the sun's photon proxy wave is a
small fraction of a millimeter.) The angular diameter of stars is too small
to measure directly; all stars appear as points even in the largest telescopes.
Because of their small apparent sizes, the diameters of stars can be mea-
sured only indirectly, by instruments such as the stellar interferometer.

Hanbury Brown's interferometer consisted of two twenty-foot search-
light mirrors mounted on railroad tracks. Each searchlight collected light
from the same star and focused it onto a photon detector. At Narrabri
signals from each photon detector were combined electronically, but the
operation of this instrument is easier to visualize if we imagine that each
mirror directs its beam of starlight to a giant phosphor screen (Fig. 7.3).
When the searchlight mirrors are close together, an interference pattern
appears on the phosphor screen, as light from one mirror shifts in and out
of phase with light from the other mirror. Still focused on the same star,
the mirrors are rolled apart. The interference pattern disappears when the
mirror separation is so large that the mirrors lie outside the photon's wave
function. Some stars' wave functions are bigger than Hanbury Brown's
railroad line, which was capable of measuring wave functions as large as
four hundred feet in diameter—the size of the photon proxy wave from
Zeta Orionis, the brightest star in Orion's belt. Stars whose angular size is
smaller than Zeta Orionis possess correspondingly larger proxy waves. The
wave functions of some very distant stars are considerably wider than the
Australian continent.

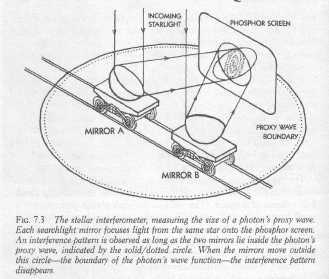
On the phosphor screen, the interference pattern is formed one photon
at a time: photons are undoubtedly point particles. Yet the pattern itself
can only be explained by something wavelike—represented by the pho-
ton's proxy wave—which is able to bounce off both mirrors at once and
come together on the screen to produce the zebra-striped pattern charac-
teristic of wave interference. Like the one-hole diffraction experiment, the
stellar interferometer demonstrates the coexistence of wave and particle
effects. Nothing but particles are ever detected directly, but the pattern of
these particles must have been caused by some sort of wave—the form
light seems to take when it is not being measured. The interferometer
actually determines the boundaries of this quantum wave and shows that
the size of such waves—the same kind of wave an atom is made of—need
not be restricted to atomic dimensions.

To understand quantum theory, as opposed to merely knowing how to
use it, we must answer two questions: 1. What does the wave function
really mean? (the interpretation question); 2. What happens during a

quantum measurement? (the measurement problem). The quantum real-
ity crisis arises because physicists have no good answers for either of these
questions. In this chapter we looked briefly at the interpretation question.
We turn next to the measurement problem.

8

"And Then
A Miracle Occurs":

The Quantum
Measurement Problem

"No language which lends itself to visualizability can describe the
quantum jumps."

---Max Born

A gravity wave is a ripple in the curvature of space-time. Einstein's general
theory of relativity predicts that gravity waves ought to be generated wher-
ever huge masses accelerate—for instance, in binary star systems. If Ein-
stein is right, gravity waves from all parts of the sky pass through the
Earth every day.

A gravity wave slightly warps every object in its path, squeezing it in
one direction and stretching it in the orthogonal direction. Because of the
ubiquity of gravity waves, every object we see is continually pulsing to the
gravitational rhythm of distant stars. However, compared to the electric
force that holds things together, gravity is exceedingly weak; consequently
the daily deformation of ordinary objects by gravity waves has escaped
detection.

Soviet Gravity Wave Detector

At Moscow University, Vladimir Braginski is looking for gravity waves by
monitoring tiny changes in the shape of a 200-pound sapphire crystal
cylinder. Braginski chose this exotic material because after being struck it
continues to quiver for a record time. Sapphire's long ringing time permits
making a maximum number of measurements before the gravity wave's
impact fades away. To isolate it from terrestrial noise, the Soviet sapphire
is suspended by wires in a vacuum chamber and cooled to near absolute
zero.

So far, Braginski and his colleagues haven't seen any gravity waves and
are working to decrease the noise in the position detectors which sense the
distortion of the sapphire rod. If they can reduce this noise by several
orders of magnitude, the Russian physicists expect to reach a point where
the sensitivity of their measurements is limited by the quantum nature of
the sapphire bar.

The sapphire crystal, considered as a quantum entity, is subject to the
Heisenberg uncertainty principle: any measurement which accurately de-
termines its position attribute must widen its momentum's realm of possi-
bility. In general the uncertainty principle does not limit how accurately
you can measure a single attribute but only restricts the mutual accuracy of
measurement of two conjugate attributes. As far as the uncertainty princi-
ple is concerned, you can make a position measurement as accurately as
you please. Since Braginski's group is only interested in the position of the
sapphire bar—more precisely just the position of the boundaries that de-
fine its shape—one would not expect them to be troubled by a variance in
the bar's momentum.

The Russians could indeed ignore the bar's momentum spread if they
planned to make only one position measurement. However, for reliability's
sake they must measure position repeatedly; the more measurements the
better. Best is when the bar's position can be monitored continually.

The first accurate position measurement induces via the uncertainty
principle a large momentum spread. For the same reason a collection of
particles with different momenta will quickly drift apart, this induced
spread in the bar's momentum soon results in a spread in the bar's posi-
tion. Momentum just happens to be an attribute whose uncertainty feeds
back into the position attribute. Braginski calls such a situation—where

theory doesn't quit when things get big and see-able. We've already met
up with starlight proxy waves bigger than parking lots. Now Russian physi-
cists reckon a king-sized sapphire as much a quantum entity as a photon of
light.

The Quantum Meter Option

I call the experimenter's ability to freely select which attribute he will
measure the quantum meter option. In the case of the Moscow gravity
wave detector, choosing to measure attribute X1 rather than position leads
to a more accurate knowledge of the sapphire bar's deformation. Exercis-
ing your meter option is a necessary part of any quantum measurement.

There are two senses in which an observer may be said to "create
reality" when he makes a quantum measurement: the first kind of reality
creation occurs whenever an observer exercises his meter option; observer-
created reality of the second kind takes place when the observer "collapses
the wave function." Most claims for an observer-created reality concern
acts of the first kind.

Because quantum theory represents a quantum entity by a wave and
attributes as waveforms, it's easy to see how the observer may be accused
of "creating reality" whenever he chooses which attribute he will observe.
The key operation in quantum measurement is selecting a waveform fam-
ily prism with which to analyze the system's wave function. Which prism
you select determines what attribute you want to look at.

Imagine doing such a waveform analysis on an ordinary wave—the traf-
fic noise from a busy street corner, for instance. Exercising our meter
option, we will analyze this noise in terms of tuba waveforms. If we want
to look at our sound sample this way, we will observe that traffic noise
consists of certain percentages of tuba notes of various frequencies con-
nected by particular phase relations. But is traffic noise really an orchestra
of tubas? Of course not.

Traffic noise supplies the raw material for this measurement, but the
choice of component waveforms is up to the observer. Finding momen-
tum in an electron wave is like finding tubas in a traffic wave. We measure
a certain electron momentum only because (thanks to the meter option)
we helped put momentum there. Electrons cannot really be said to have
dynamic attributes of their own. What attributes they seem to have de-
pends on how we choose to analyze them. A clock comes apart in only one

way: it's made of definite parts. A wave, on the other hand, doesn't have
parts; you can divide it up any way you please. However, none of these
divisions is there to begin with; the kind of parts a wave seems to have
depends on how we cut it up. The world's wave nature makes us in a
certain sense co-creators of its attributes.

There is, however, one sense in which a quantum system may be said to
possess attributes of its own. This is the same sense in which traffic noise
possesses its own identity no matter how we choose to analyze it. Traffic
noise is not made by tubas, it is made from traffic. If we analyzed such
noise with a traffic-waveform prism, it would not split into components. In
Chapter 5, I called such prisms which do not split the waveshapes they
analyze "kin prisms."

Suppose we analyze an electron beam with a momentum prism and its
proxy wave does not split. This means that its wave function is a pure sine
wave (quantum code for momentum). Experimentally we would observe a
beam of such quons to possess a single precise value of momentum. In this
special case we could say that every electron in the beam has a specific
momentum, which the observer does not create. In other words, in the
exceptional case of observation with a kin prism, we might say that the
experimenter is seeing not what he put in but what is really there. How-
ever, although these electrons seem to possess momentum in a manner
reminiscent of classical objects, none of their other attributes is single-
valued. All the other attributes come about via the quantum meter option
—observer-created reality of the first kind.

To measure a quon beam whose dynamic attributes are single-valued is
a relatively rare occurrence. Most quantum measurements give some
spread in their outcomes. For these cases the observer may be said to
partially create the attributes he observes in much the same way that we
can find tuba waveforms in traffic noise if we look for them. Using the
synthesizer theorem, we can express a quon's situation in terms of an
infinity of different attribute waveforms; the choice is up to the observer.
Physicists choose certain attributes so often to characterize physical sys-
tems that they deserve to be called major attributes. All others I call minor
attributes.

In configuration space, where the waveforms dwell which represent a
quon's external motion, the major attributes are position and momentum.
Minor attributes in configuration space include the fanciful "piano attri-
bute" and Braginski's QND attributes X1 and X2.

In spin space, where the waveforms dwell which represent a quon's

internal motion, the major attributes are the spin orientations Sx, Sy, Sz in
three orthogonal directions. For light and many other quantum entities,
the most important minor attribute in spin space is polarization.

The Polarization Attribute of a Light Beam

As a concrete example of the quantum measurement problem, let's look at
how an experimenter might go about measuring a light beam's polariza-
tion. Polarization is the simplest type of dynamic attribute because it can
take only two possible values. One less value would turn it into a static
attribute. However, despite its simplicity the polarization attribute is com-
plex enough to illustrate the full range of quantum perplexities.

Polarization is an attribute connected with a particular direction in
space. For each direction a single photon has only two options: either it is
entirely polarized in that direction or it is entirely polarized at right angles
to that direction. The only polarization directions that concern us here are
the orthogonal—those at right angles to the light beam's direction of
travel. To visualize these polarization directions, imagine the light beam
encircled by a clock dial. The hour hand's directions represent all possible
polarization directions. If we let twelve o'clock equal zero degrees, these
polarization directions can be described either by a clock time or by an
angle or by conventional direction labels such as horizontal or vertical.
Twelve o'clock, for instance, stands for vertical polarization; three o'clock
for horizontal polarization. Only half the clock face represents a unique
polarization: nine o'clock and three o'clock, for example, both represent
the same direction, namely horizontal polarization.

To visualize a polarization measurement, imagine that you are a batter
standing on home plate trying to hit photons that the pitcher is throwing.
(This pitcher's fast ball is really fast: it travels at the speed of light.) You
hold your bat at a particular angle and if the photon is polarized at that
angle, it's a hit; otherwise it's a miss and you know that the photon was
polarized perpendicular to your bat.

A binary outcome connected with a single direction is the most that
quantum theory permits you to know about the polarization attribute of a
single photon. All you can learn when you make such a measurement is
whether the photon is polarized along the direction of your choice (hit), or
at right angles to your chosen direction (miss). Your quantum meter op-
tion for a polarization measurement consists of choosing for each photon

In the laboratory the light beam goes through a calcite crystal whose
optic axis is pointing in a particular direction. Calcite is a birefringent
crystal: it divides light into two beams, the up beam consisting of photons
polarized along the optic axis, the down beam consisting of photons po-
larized at right angles to the optic axis. More about this remarkable min-
eral may be found in the appendix to this chapter.

To record whether a particular photon actually goes up or down, a
simple photon detector is placed in each channel. This detector consists of
a phosphor screen that gives off a flash of light when excited by a photon,

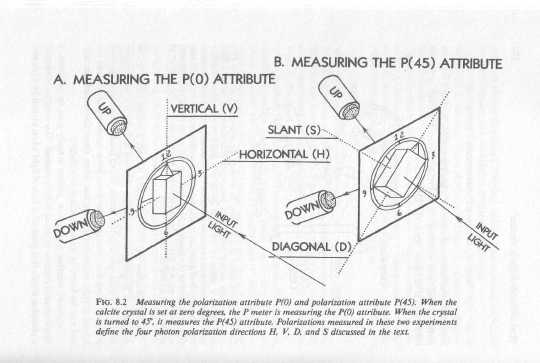
plus a lens that gathers this phosphor light and focuses it onto a sensitive
plate (similar to an element of a solar cell) which produces an electric
pulse in response to light. Fig. 8.1 shows a complete polarization meter set
to measure the polarization attribute P(0): the calcite's optic axis is aligned
at zero degrees. The electric pulse from the photon detector is amplified
and sent to a recorder (not shown) which prints a U or a D on a record
tape depending on whether the up or down detector fired for that particu-
lar photon. Fig. 8.2 shows this polarization meter in two of its many
possible settings. When the calcite's axis is set at twelve o'clock (zero
degrees), the Polarization meter measures attribute P(0): up and down
signals from the counters correspond to V and H photons respectively.
When the calcite's axis is set at 2:30 o'clock (45 degrees), the Polarization
meter measures attribute P(45): up and down signals now correspond to D
and 5 photons.

Six Variations on the Quantum Measurement Problem

After this brief digression into experimental physics we are ready to tackle
the measurement problem. Start with a pure D-polarized beam and mea-
sure its P(0) attribute with a calcite crystal set at zero degrees. The beam
divides into equal numbers of H and V photons. But what's actually going
on here when one beam splits into two?

In terms of this simple experiment—the measurement of H/V polariza-
tion on a pure D-polarized beam—it's easy to state the quantum measure-
ment problem. In fact since this problem is so important for the quantum
reality question I express it here in six different ways. Although simple to
state, this problem is not so easy to solve. All solutions to the measurement
problem that physicists have so far come up with either lead to bizarre
realities and/or sanctify some aspect of the measurement act.

It's hard to believe that nature endows the act in which humans make
contact with quantum entities with a special status not granted to all the
other interactions in the universe. Any interpretation of measurement
which attributes supernatural powers to the act itself must be regarded
with suspicion. There's something philosophically fishy about a measure-
ment-centered cosmos. How the world appears to us must certainly de-
pend on how we measure it, but it's absurd to believe that how the world
actually is is determined by human observational capacities. "Measure-
ments are happenings," says U.S. Navy physicist T. E. Phipps, "but they

are the least of the happenings that go on in the world. It demeans
physics, not to mention the world, to shackle physics with its own instru-
mental tools through any linguistic implication that measurements are all
that happens in the world."

Here then are six variations on the quantum measurement problem that
has baffled physicists for more than half a century.

1.   Physicists can't represent a quantum system's physical situation in clas-
sical terms; they express it in terms of quantum possibility waves. On the
other hand, the measuring device and its result can't be expressed in terms
of possibilities, but like any other aspect of human experience must be
described in terms of a concrete classical actuality. The quantum measure-
ment problem is this: at what point between the input photon and the
observation of a definite mark (D, for instance) on the output tape does
the transition occur between these two strikingly different styles of exis-
tence? Where do we put the "cut" which divides the quantum and classical
world?

2.  According to the orthodox ontology, because they are all in the same
quantum state, the physical situation of each D photon is identical to that
of every other. However, the results printed on the measurement tape are
not all the same. At what point in the measurement process do identical
quantum entities develop differences?

3.  According to the orthodox ontology, after being split by the crystal,
each D photon dwells in a state of pure possibility. But the measurement
results themselves are actual facts, not possibilities. At what point in the
machinery does possibility change into actuality?

4.  According to the orthodox ontology, each D photon takes both paths
through the analyzing crystal and simultaneously occupies both the H and
V channels. Yet for each photon only one channel actually fires (either H
or V but not both) and prints a character on the output tape. In the
process of quantum measurement, when do two paths turn into one? And
what happens to the path not taken?

5.  According to the orthodox ontology, our relationship to a quon's physi-
cal situation after it's split by the analyzing crystal is one of quantum
ignorance: we do not know the difference between quon #123 and quon
#137 because no such difference exists in nature. Not even God can tell
apart two quons in the same state. Yet after 1,000 photons have been

measured we are convinced that the measurement tape actually contains
marks that are not the same for each photon. In other words, before we
look at the tape, our relationship to these results is one of classical igno-
rance. How and when does quantum ignorance turn into classical igno-
rance?

6. My final variation on the theme of quantum measurement poses the
question: how and when does the wave function "collapse"? We will learn
later about the process of wave function collapse in connection with John
von Neumann's all-quantum model of the measurement act.

Notice that the measurement problem seems mostly to arise from tak-
ing the orthodox ontology seriously and trying to reconcile its teachings
with what is actually observed. One easy solution to the QMP might be to
simply deny the orthodox ontology and accept a neorealist model of the
world. There is no measurement problem in neorealist models, but they
have another problem instead. Bell's theorem tells us that no neorealist
model will work unless it contains real but invisible faster-than-light force
fields, a situation most physicists consider unacceptable.

Those who embrace the orthodox ontology (the majority of physicists)
fall into two camps: the followers of Bohr and Heisenberg (Copenhagen-
ists) and the followers of John von Neumann.

The Copenhagen Picture of Quantum Measurement

The Copenhagenists consider ordinary experience the primary unanalyz-
able reality in terms of which they explain the atomic realm. For Bohr and
Heisenberg the world is forever divided into two types of reality: quantum
reality which we can never experience, and classical reality which is all
that we can ever experience. Quantum theory is not a representation,
much less a description, of quantum reality, but a representation of the
relationship between our familiar reality and the quon's utterly inhuman
realm. As Heisenberg puts it: "The Copenhagen Interpretation regards
things and processes which are describable in terms of classical concepts,
i.e., the actual, as the foundation of any physical interpretation." Harvard
physicist Wendall Furry echoes Heisenberg's elevation of ordinary reality
to top-dog status: "[In the Copenhagen interpretation] the existence and
general nature of macroscopic bodies and systems is assumed at the outset.

These facts are logically prior to the interpretation and are not expected to
find an explanation in it."

In other words, the Old Physics attempted to explain macroscopic ob-
jects in terms of the atoms which make them up; the New Physics ex-
plains atoms in terms of macroscopic objects. In this inverted Copenha-
gen scheme, there is a sense in which atoms are made of measuring
instruments and not the other way around. As Heisenberg writes: "Only a
reversal of the order of reality as we have customarily accepted it has made
possible the linking of chemical and mechanical systems of concepts with-
out contradiction." Of course Copenhagenists believe that their instru-
ments are made of atoms just like everything else, but this manner of
thinking (instruments made of atoms) can be carried only so far.

A curious feature of the Copenhagen interpretation is that it considers
both the atom and the measuring device to be incomprehensible. We
cannot understand the quantum world because its nature is utterly alien to
human thought; we cannot explain the classical world because quantum
theory—the physicist's only basis for explaining anything today—simply
takes the existence of the classical world for granted. In Furry's words, the
classical world is "logically prior" to quantum theory and "is not expected
to find an explanation in it." Quantum theory predicts how a classical
measuring instrument will respond to a quantum system, but the theory
itself does not contain such measuring devices—nothing in there but
proxy waves. Fortunately for the practice of physics, each of us is born into
a world already inhabited by these inexplicable measuring devices: your
eye is one example.

According to Bohr, quantum theory describes neither the quantum sys-
tem nor the measuring device. Quantum theory applies to the relationship
which exists between these two conceptually opaque kinds of being. Since
the measuring device cannot in principle be analyzed, it's the perfect
place to put the solution to the measurement problem. In the Copenha-
gen interpretation, all the mysterious transitions between the quantum
and classical kinds of being occur inside the measuring device or more
properly at the boundary between measuring device and quantum system.
We see that the Copenhagen interpretation does not so much solve the
measurement problem as conceal it. It sweeps this problem under the rug,
into the one place in the world inaccessible to human scrutiny—the in-
sides of measuring devices.

The Von Neumann Picture of Quantum Measurement

The fact that Copenhagenists must divide the world into a classical part
(measuring device) and a quantum part (measured system) displeased John
von Neumann. The world obviously has only one nature, and that nature is
not classical. To reflect the world's necessary unity, von Neumann under-
took to represent the whole world one way: he symbolized both the system
and the measuring device with proxy waves. Von Neumann's world is
entirely quantum—there's not a bit of classical physics in it. Von Neu-
mann described this all-quantum picture of the world in his quantum
bible, Die Grundlagen. It works. It's possible to represent the entire world
(both system and measuring device) in terms of proxy waves if you make
one assumption. Von Neumann's crucial assumption is the basis of my
sixth (and last) variation on the quantum measurement problem.

As Feynman showed in his sum-over-histories version of quantum the-
ory, one way to think about what unmeasured quons are doing is to imag-
ine that each quon takes all paths. Feynman's picture amounts to a sort of
quantum law of motion, analogous to Newton's law of motion for classical
objects.

Each quon moves from one state of being to the next according to a
ruthless territorial imperative demanding that it occupy all its possibilities
at the same time. The fact that most of these paths are obliterated by
destructive interference in no way alters a quon's primal orders: fill the
Earth with your essence! The law of the realm ensures that no matter how
many of a quon's possibilities are destroyed by wave interference or by
measurement, a certain minimum remnant will always remain. A quon
always possesses, no matter what its circumstances, a realm of possibilities
at least equal to Planck's constant of action.

This is the quantum law of motion: Increase and multiply: starting from
your inviolable realm, take all possible paths open to you. The natural
evolution of a quon's proxy wave is to expand without limit. However, in
the measurement act a quon can't realize all its possibilities because only
one measurement result actually happens. Therefore at some point be-
tween its creation in the quon gun and its registration as an experimental
result, a quon must repudiate the universal law of motion, halt its unbri-
dled natural expansion, and contract into a single possibility corresponding
to the single observed measurement result.

Thus, according to von Neumann, a quon follows not one law of motion
but two. Everywhere in the universe, proxy waves are expanding (called
"Type I process" by von Neumann). However in the measurement act,
and nowhere else, proxy waves contract to a definite result (a so-called
"Type II process"). After contraction these entities are still proxy waves;

they never turn into classical objects. Consequently when one attribute's
realm suddenly contracts, its realm of conjugate possibilities explosively
expands.

Physicists call von Neumann's Type II process "the collapse of the wave
function"; it's also called the "quantum jump." Von Neumann's all-quan-
tum description will not work unless such a collapse really occurs as a
physical process in every quantum measurement. My sixth variation on
the measurement problem is this: How and where does the wave function
collapse occur?

Where Does the Wave Function Actually Collapse?

Von Neumann was understandably anxious to find a natural location for
the wave function collapse, which is essential for his interpretation of
quantum theory. He systematically examined the measurement process for
clues for a special feature of measurement which might give rise to a Type
II process. He visualized the measurement act as broken into small steps
called the von Neumann chain, stretching from the quon gun to the
observer's consciousness where the measurement result is ultimately regis-
tered. Each process in between is a link in von Neumann's chain. A
solution to the measurement problem, according to Swiss chemist Hans
Primas, would consist of "severing von Neumann's chain at the first true
measurement act." In other words, where in fact is a quantum measure-
ment actually accomplished?

While searching for a natural place to break his chain, von Neumann
proved an important mathematical fact that deepens the mystery of mea-
surement. Von Neumann showed that as far as final results are concerned,
you can cut the chain and insert a collapse anywhere you please. This
means that the results themselves can offer no clues as to where to locate
the division between system and measuring device.

Von Neumann's version of the measurement problem reminds me of a
cartoon by Sidney Harris, an artist who specializes in poking fun at scien-
tific foibles. A mathematician has outlined his work on the blackboard for
one of his colleagues. The argument consists of the usual incomprehensi-
ble symbols, but near the end there's a gap in which he's written, "And
then a miracle occurs." The math then resumes and proceeds to its logical
conclusion. The mathematician's colleague is pointing to the gap and
saying, "I think you should be more explicit here in Step 2."

On each side of the wave function collapse, von Neumann erects im-
peccable mathematical structures familiar to quantum physicists—the
world expressed as proxy waves. However, separating these two sides of the
argument—the world unmeasured and the measured world—is a logic gap
in which von Neumann effectively writes, "And then a miracle occurs."

Von Neumann could not find a natural place to locate his "miracle."
Everything, after all, is made of atoms: there's nothing holy about a mea-
suring instrument. Following the von Neumann chain, driven by his own
logic, in desperation von Neumann seized on its only peculiar link: the
process by which a physical signal in the brain becomes an experience in
the human mind. This is the only process in the whole von Neumann
chain which is not mere molecules in motion. Von Neumann reluctantly
came to the conclusion (Quantum Reality #7) that human consciousness
is the site of the wave function collapse.

This direct intervention of consciousness in every measurement is what
I call "observer-created reality of the second kind" to distinguish it from
the mild kind of observer-created attributes entailed by the quantum
meter option. In von Neumann's consciousness-created world, things (or
at least their dynamic attributes) do not exist until some mind actually
perceives them, a rather drastic conclusion but one to which this great
mathematician was forced by sheer logic once he decided to take the
quantum measurement problem seriously.

Fig. 8.3 illustrates three major approaches to what goes on in a quantum
measurement: 1. Bohr's Copenhagen interpretation divides the world
into quantum and classical realms—both incomprehensible—whose rela-
tionship is represented by a fictitious proxy wave; 2. Von Neumann's all-
quantum picture represents both quon and M device with proxy waves
which are connected by the so-called wave function collapse; 3. David
Bohm, Louis de Broglie and other neorealists describe the physicist's
world—consisting of systems and M devices—as being made solely of
particles connected by (superluminal) waves.

Each of these approaches to quantum measurement has its drawbacks;
none gives a completely satisfactory picture of the measurement act. The
Copenhagen interpretation endows the measuring instrument with magi-
cal properties—the ability to reduce possibility to actuality, for instance—
while removing such instruments in principle from logical analysis. Von
Neumann restores the measuring instrument to an equal status with the
rest of the world but transfers its magical properties to a mysterious and
elusive event, the wave function collapse. The neorealist model of reality

sanctifies neither measuring device nor measurement act; neorealist mea-
surements are just ordinary interactions. However, the price for this neore-
alist solution to the QMP is the necessary existence of invisible superlumi-
nal force fields.

Because of the unsatisfactory state of the measurement problem, many
physicists have attempted to find solutions less drastic than those of Bohr,
von Neumann, and Bohm.

Do Quantum Entities Possess Fuzzy Attributes?

In the early days of quantum theory, Erwin Schrodinger wondered
whether one might be able to devise an all-quantum world like von
Neumann's with this difference: although measuring devices are fully
quantum, their quantum effects are so small that for all practical purposes
they act classically. Schrodinger's proposal depends on the fact that
Planck's constant is so tiny that on the scale of ordinary objects it is
effectively zero.

Schrodinger proposed that the attributes of measuring devices as well as
atoms are intrinsically ill defined, but the fuzziness of measuring devices is
so small (on the order of Planck's constant) that to human senses they
appear to possess well-defined attributes. In other words, Schrodinger sug-
gests that a single atom as well as an individual M device possesses not one
momentum but a range of momenta—momenta that exist not merely in
potentia but in actuality. Schrodinger's proposal seems plausible when one
realizes how small Planck's constant actually is compared with ordinary
acts.

The dimensions of the quantity "action" in physics is energy times time
(erg seconds). One erg second is not very large—about equal to the
amount of action in a blink of your eye. Planck's constant of action is
incomprehensibly smaller than an eye blink. It is one erg second divided
by a billion . . . divided by a billion . . . then divided once more by a
billion. Planck's constant is about 1 X 10[to the-27th power] erg seconds.

Astronomers reckon the whole starry universe to be approximately 10[to the 27th power]
centimeters wide—the distance light has traveled since the universe be-
gan. One centimeter is about the size of a sugar cube. A line of sugar
cubes stretching across the universe would contain about 10[to the 27th power] cubes. This
row of cubes spans not just the solar system, not just our local galaxy or
galactic cluster, but the entire physical universe—everything there is.

One eye blink contains as many quanta of action as there are sugar
cubes in that long white line. So minuscule is the scale of quantum events
compared to the actions of everyday life that it's a wonder humans ever
found out about the quantum world at all. If, as Schrodinger conjectured,
the attributes of measuring devices were fuzzy to the extent of a few
quanta, this fuzziness would be utterly undetectable, like a firefly in the
glare of the sun. For atoms whose entire beings are composed of just a few
quanta of action, Planck's constant is a big deal. For macroscopic instru-
ments with actions on the scale of eye blinks, a few quanta more or less
make no noticeable difference.

Despite the fact that their fuzziness could never be directly observed,
Schrodinger concluded that measuring devices cannot possess fuzzy attri-
butes. He argued that even though M devices would have realms of possi-
bility too small to measure, it's easy to imagine experiments which split
these tiny realms into two disjointed domains, each of which has very
different macroscopic consequences.

For instance, in our polarization experiment the realm of possibility of
each D photon is exactly cleaved in two by the H/V crystal. This photon,
after passing through the crystal, becomes a superposition of V and H
photons which are spatially separated. According to the laws of quantum
motion (expand to fill all possibilities) this state evolves into a state in
which both the up and down counters are triggered at the same time by a
single photon. In this experiment the fuzziness of the microworld spreads
in such a way that it engulfs the whole apparatus: now two large pieces of
phosphor, glass and metal are forced into a quantum superposition.

To dramatize his argument, Schrodinger expanded this measuring de-
vice to include a cat. Imagine, he says "a hellish device": the outputs of
the up and down detectors go into a closed box in which an innocent cat
dwells. If the up counter fires, the cat lives; if the down counter fires, the
cat dies. Only one photon enters the apparatus. What happens to Schro-
dinger's cat?

Because of Schrodinger's assumption that macroscopic objects possess
fuzzy attributes, the photon's two simultaneous paths lead to the counters'
two simultaneous triggerings, which results in both an up and a down
signal which makes the cat both alive and dead at the same time!

The photon's realm is only one quantum wide, but a crystal of calcite is
keen enough to split it. This split spreads to the photon detectors and
ultimately to Schrodinger's cat, which must now exist—if his conjecture is

correct—in a peculiar state: half-dead cat/half-live cat. And as my col-
league Bruce Rosenblum remarks, "This does not mean the cat is sick."

Unless our perceptions are terribly mistaken, it is absurd to attribute
such a bizarre form of existence to a cat or to a measuring device: nobody
has ever seen a superposition of up/down measuring devices, let alone
live/dead cats, and no one ever will. Schrodinger concludes that we are
simply mistaken if we believe that measurement devices possess slightly
fuzzy attributes. This attempted solution to the measurement problem is a
dead-end street.

Somewhere between crystal and cat, the quantum rules have to change:
the system's spread-out attributes must somehow turn into one unique
actuality. Schrodinger's informal argument suggests what von Neumann
proved more rigorously with his mathematics: if the whole world is de-
scribed quantum-mechanically, in terms of proxy waves, then somewhere
between the quon source and final result a "wave function collapse" must
occur. If the wave function never collapses but always expands to fill its
open possibilities, then Schrodinger's hellish device shows how easy it
would be to produce cats that were both alive and dead at the same time.

Schrodinger's argument against fuzzy attributes depends on the fact
that in this experiment we know (because each typed output mark is
either up or down, never both) that the cat will either be alive or dead but
not both. We assume here that as far as its macroscopic behavior goes, a
cat is no different from a typewriter. Although we have good reason to
believe that the cat always exists in a definite state of health in this
experiment, quantum theory seems to permit in principle other experi-
ments in which the outcome is not so clear-cut. Vladimir Braginski's
sapphire bar, for instance, is larger than any cat and exists, after the
Russians exercise their meter option in favor of attribute X1, in a quantum
state consisting of half momentum, half position waves summed with a
definite phase: an unusual situation for a "classical" object. Perhaps we've
never seen a live/dead "Schrodinger cat" only because we don't know how
to look for one.

At a recent conference on quantum chemistry, physicist Frederik Be-
linfante, author of an important survey of hidden-variable models of real-
ity, commented that if quantum theory permitted Schrodinger catlike
phenomena to happen, one could not only kill cats with quantum ma-
chines but also bring them back to life. He predicted that quantum theory
might someday become an important branch of veterinary medicine.

From what we know about quantum theory, it's easy to see how to build

a machine for reviving dead cats. All we have to do is precisely measure an
attribute which is conjugate to the live/dead attribute; the uncertainty
principle does the rest. Start with a cat in a well-defined dead state. Exer-
cise your meter option in the following manner. Put this cat through a
filter which only passes cats with a well-defined value of an attribute called
"diagonal cat"—an attribute conjugate to the live/dead attribute. Half
the (formerly dead) cats that pass such a filter will be alive. If your cat is
still in the dead state after passage through the diagonal-cat filter, put him
through again. This filter has only a 50 percent cure rate but it can be used
over and over.

Can Phase Randomization Collapse the Wave Function?

In Schrodinger's experiment the photon takes both paths but the cat
doesn't. What special feature of macroscopic objects prevents a cat from
splitting into a superposition of possibilities? Some physicists believe that
phase randomization is what separates cats from photons. Cats are quan-
tum entities too, but their phases are mixed up; a photon's phase on the
other hand is nice and orderly. Does the process of wave function collapse
occur whenever a system's phases become sufficiently random?

It is not difficult to find mechanisms for phase randomization inside
measuring devices. Italian physicists Antonio Daneri, Angelo Loinger, and
Giovanni Maria Prosperi show that the thermodynamics of large bodies
can randomize phases. Russian physicist Dmitri Blokhintsev shows that
the process of amplification, which makes a quantum process visible to
human eyes, will inevitably randomize quantum phases. Others blame
phase randomization on the irreversible process involved in making a rec-
ord. Physicists H. Dieter Zeh and Wojciech H. Zurek show that interac-
tions with the environment are continually randomizing the phases of mac-
roscopic objects. In their view, cats and photon counters don't split
because the environment is always watching them.

Von Neumann proved that you could put the wave function collapse
anywhere between source and observer without changing the results. This
means that the collapse site cannot be located by appeal to experiment.
However, if you put the collapse too close to the quon source you will spoil
the results of other experiments which you could have done on the same
quon. If you collapse the wave function prematurely, these other experi-

ments will give the wrong results. The results of these other experiments
allow us to exclude certain locations for the collapse site.

For instance, suppose we assume that the input D photon collapsed
inside the analyzing crystal: instead of taking both paths (Vand H), it just
takes one. This collapse location is consistent with the results that for each
photon only one symbol (Up or Down) is typed on the output tape, but
such a premature collapse will not agree with another experiment we can
do which determines whether a photon takes one path or two.

Using mirrors, for instance, we can combine light from the two crystal
channels and look for the wavewise interference of polarization attributes
which is characteristic of quons that are taking both paths. If we see such
interference, then we know the wave function has not yet collapsed. In
this case, when we combine beams we see interference effects between
polarization attributes: immediately after the crystal, the photon evidently
takes both paths.

Let's follow the von Neumann chain a bit farther. Does the wave func-
tion collapse when the photon excites a phosphor molecule? Most physi-
cists would argue that it does not. After the phosphor is excited it returns
to its ground state: it does not make a record of the photon's presence. If
we were clever enough, we could make the light from both the up and the
down phosphors interfere, and verify that when it passed the phosphors
the measurement process was still split.

What about the next step in the von Neumann chain? The phosphor
light (still presumably split into two simultaneous possibilities) passes
through a pair of focusing lenses. One well-known property of lenses and
mirrors is that they preserve phases: if they did not, they could not form
clear images. So it's unlikely that the wave function collapses at the lenses.

The light-sensitive screen is next in the von Neumann chain. Here light
interacts with the electron wave in a silicon crystal, promoting it to a
higher energy state. Since the up electron wave is in a physically different
crystal from the down electron, it is difficult to get them to interfere.
However, we could imagine doing the same experiment using a single slab
of silicon instead of two separate detectors. Again in principle, we could
observe interference effects between the two electron excitations in the
silicon crystal.

It seems that if you are sufficiently ingenious you can push the site of
the wave function collapse as close as you wish to the observer. However,
this experimental method depends on the fact that the waves in each path
have well-defined phases.

This particular test for premature wave function collapse depends on
the experimenter's ability to bring the split beams together to show an
interference pattern. But we saw in Chapter 5 that when waves add with
random phases their interference pattern disappears. So if phases become
random somewhere along the line, then we cannot apply this test for wave
function collapse. This does not in itself mean that once the waves be-
come random, they have collapsed; it means only that this way of testing
for premature collapse will not work anymore.

Besides making it difficult to test for the presence of simultaneous pos-
sibilities, the randomization of phases has another peculiar consequence
for quantum theory which we can understand by looking at what phase
randomization does to ordinary waves. We recall from Chapter 5 that
ordinary waves added with definite phases do not conserve energy (ampli-
tude squared) everywhere, but show local regions of energy surplus and
deficit. However, when the waves are randomized energy is conserved
everywhere: energy in one beam adds like ordinary arithmetic to energy in

the other beam.

The same thing happens to randomized quantum waves, but here prob-
ability (quantum amplitude squared) takes the place of energy in ordinary
waves. Quantum waves added with definite phase do not conserve proba-
bility everywhere, but show local regions of probability surplus and deficit
(interference of attributes). However, when these waves are randomized,
probability is conserved everywhere: probability in one beam adds like
ordinary arithmetic to probability in the other beam. In other words,
when a quantum wave's phase is randomized, its corresponding probabili-
ties combine exactly like classical dice probabilities.

This remarkable fact, that after phase randomization quantum probabil-
ities behave numerically the same as classical probabilities, is used by some
physicists to argue that once phase randomization has occurred, quantum
and classical probabilities are conceptually the same. That is, they claim
that randomization of phase by itself is sufficient to bring about wave
function collapse and convert a situation in which a quon take both paths
(quantum ignorance) to a situation in which it takes only one (classical

ignorance).

Although phase randomization can certainly scramble paths, it is diffi-
cult to see how it can destroy them: the law of the realm guarantees that a
quon's possibilities can never be reduced below an action quantum. Just as
no amount of mixing will turn black sand and white sand into gray sand,
so no amount of phase randomization will turn two paths into one. When-

ever one looks closely at claims that randomization by itself collapsed the
wave function, one always finds that the collapse—the conceptual transi-
tion from quantum to classical ignorance—had to be put in "by hand."
Although phase randomization may muddy the waters, it cannot hide the
fact that there is always a place in the analysis where one simply admits,
"And then a miracle occurs." Phase randomization is evidently present in
all measurement situations but by itself does not constitute a "measure-
ment." The scrambling of quantum phases seems to be a necessary but
not sufficient condition for wave function collapse.

Although phase randomization can destroy some aspects of wave behav-
ior and mimic to some extent the behavior of classical probability, certain
aspects of wave behavior are immune to its effects. We saw for instance in
Chapter 5 that when the Airy pattern was randomized, interference was
destroyed but diffraction survived. The spectral area code (Heisenberg
uncertainty principle) is another wave property that remains valid whether
phases are orderly or not. Perhaps there are other innate wave properties
yet to be discovered which survive phase randomization and whose quan-
tum analogs may help us penetrate deeper into the mystery of the collapse
of the wave function: where the strange world of the quantum quietly
turns into the world of everyday life.

Appendix: Calcite, a Crystal That Splits Photons

At the time of Newton, a sailor discovered in Iceland a transparent min-
eral with remarkable optical properties. Iceland spar, more commonly
called calcite, is birefringent: it bends light along two different paths de-
pending on its polarization.

This crystal's sensitivity to polarized light suggests that the mysterious
"sailing stone" mentioned in the Icelandic sagas may have been a species
of calcite. As a direction finder, lodestone would be useless so close to the
Earth's magnetic pole. Sailors in such high latitudes probably steered by
the stars and sun. But during the long summer twilights the sun is often
out of sight below the horizon. Because light from the sky is partially
polarized in a particular sun-centered pattern, Viking sailors could have
fixed the sun's direction at sea by observing skylight polarization through a
calcite crystal. Although we will probably never know for sure, this crystal,
so useful in modern reality research, may long ago have helped Norsemen
discover America.

When a beam of light goes into a calcite crystal, two beams come out.
One of these beams is called the ordinary ray because it obeys the conven-
tional laws of optics. These laws say, for instance, that a beam of light
striking a transparent surface head-on does not bend. Calcite's second
beam is named the extraordinary ray because it flouts these optical regula-
tions. For instance when light strikes calcite head on, the ordinary ray goes
straight but the extraordinary ray bends.

This strange schizophrenic behavior of light in calcite challenged the
best minds of the seventeenth century. Dutch physicist Christian
Huygens gave the first scientific explanation of this marvelous crystal.
Huygens analyzed calcite light by conceptually breaking it up into little
spherical wavelets, a technique which inspired Feynman's sum-over-histo-
ries version of quantum theory three centuries later.

The key to calcite's behavior is its optic axis—a special direction, indi-
cated by an arrow in Fig. 8.1, that runs through the crystal. Light po-
larized parallel to this axis travels through the crystal normally. Light
polarized at right angles to the optic axis takes a deviant route—the ex-
traordinary way. If the optic axis is oriented vertically, vertically polarized
photons take the ordinary path (up), horizontally polarized photons go the
extraordinary way (down).

In the modern view, calcite cleaves light in two because its crystal
structure is sensitive to the difference between the quantum waveforms
associated with the polarization attributes. According to quantum theory,
the calcite crystal is a window into the microcosm: its double beam is
indicative of the two-valuedness of the photon's polarization attribute.

9 - Four Quantum Realities

"Physics takes its start from everyday experience, which it contin-
ues by more subtle means. It remains akin to it, does not transcend
it generically; it cannot enter into another realm. Discoveries in
physics cannot in themselves—so I believe—have the authority of
forcing us to put an end to the habit of picturing the physical
world as a reality."

---Erwin Schrodinger

Quantum theory works like a charm: it correctly predicts all the quantum
facts we can measure plus plenty that we can't (such as the temperature of
the sun's interior) or do not care to (the electron's "piano attribute," for
instance). This theory has passed every test human ingenuity can devise,
down to the last decimal point. However, like a magician who has inher-
ited a wonderful magic wand that works every time without his knowing
why, the physicist is at a loss to explain quantum theory's marvelous suc-
cess.
What does it mean to "explain" a theory? Just imagine what one would

like to know about the magician's wand, namely the hidden reality respon-
sible for its magical operation. Quantum theory is more than a lucky gift
out of the blue; this theory's unprecedented predictive power suggests that
it makes contact with some real features of the physical world. An "expla-
nation" of quantum theory would tell us what sort of world we live in that
allows such a curious wave-mathematical technique to foretell this world's
gestures in such precise detail.

Quantum theory resembles an elaborate tower whose middle stories are
complete and occupied. Most of the workmen are crowded together on
top, making plans and pouring forms for the next stories. Meanwhile the
building's foundation consists of the same temporary scaffolding that was
rigged up to get the project started. Although he must pass through them
to get to the rest of the city, the average physicist shuns these lower floors
with a kind of superstitious dread. New York University professor Daniel
Greenberger, speaking at a recent Festschrift, speculated about why most
physicists avoid the quantum reality question:

"This sudden success on a grand scale, after a generation of desperate
striving by great minds, lends a heroic, even mythic, quality to the history
of [quantum theory]. But, inevitably, it has also led to a sensitivity on the
part of physicists, a kind of defensiveness, ultimately arising from the fear
that the whole delicate structure, so painstakingly put together, might
crumble if touched. This has tended to produce a 'Let's leave well enough
alone' attitude, which I believe contributes to the great reluctance most
physicists have to tinker with, or even critically examine, the foundations
of quantum theory. However, fifty years have gone by and the structure
appears stronger than ever."

Physicists' reality crisis consists of the fact that nobody can agree on
what's holding the building up. Different people looking at the same
theory come up with profoundly different models of reality, all of them
outlandish compared to the ordinary experience which constitutes both
daily life and the quantum facts. Physicists differ over which parts of this
theory they will take seriously and which parts they will ignore as empty
formalism having no counterpart in the real world. Which different pic-
ture of quantum reality you end up with depends on what parts of quan-
tum theory you take seriously. In this chapter and the next I examine how
the eight major quantum realities arise from the selective emphasis of
certain features of quantum theory and the neglect of others.

Quantum Reality #1: The Copenhagen interpretation, Part I. (There is
no deep reality.) The Copenhagen interpretation, developed mainly by

Bohr and Heisenberg, is the picture most physicists fall back on when you
ask them what quantum theory means. Copenhagenists do not deny the
existence of electrons but only the notion that these entities possess dy-
namic attributes of their own. Although an electron is always measured to
have a particular value of momentum, it is a mistake, according to Bohr,
to imagine that before the measurement it possessed some definite mo-
mentum. The Copenhagenists believe that when an electron is not being
measured, it has no definite dynamic attributes.

Quantum theory was developed almost solely by Europeans. J. Robert
Oppenheimer, one of the few Americans to have participated in Bohr's
Copenhagen Institute, here explicitly denies the existence of the major
attributes with which classical physics described a particle's external mo-
tion: "If we ask, for instance, whether the position of the electron remains
the same, we must say 'no'; if we ask whether the electron's position
changes with time, we must say 'no'; if we ask whether the electron is at
rest, we must say 'no'; if we ask whether it is in motion, we must say
'no.' "

Some physicists confuse the Copenhagen doctrine with a pragmatic
interpretation of quantum theory. The pragmatist regards any theory as a
mere mathematical machine for generating numbers which he then com-
pares with experiment. A pragmatist is concerned with results, not reality.
The pragmatist refuses on principle to speculate about deep reality, such a
concept being meaningless from his point of view. Pragmatism is an intel-
lectually safe but ultimately sterile philosophy.

A pragmatist would refuse on principle to comment on the existential
status of an unmeasured electron's attributes. No timid pragmatists, these
students of Bohr! The Copenhagenists claim not that such attributes are
meaningless but that they are nonexistent. They base their conclusions
about an unseen quantum reality not on some abstract philosophical prin-
ciple applicable in all cases but on the specific structure of quantum theory
itself. Some theories of the world (Newtonian mechanics, for instance)
allow us to believe or not that unobserved entities possess their own attri-
butes. Quantum theory, according to the followers of Bohr, does not per-
mit us this option.

Copenhagenists take as the central clue to the nature of the quantum
world the uncertainty principle, which limits humans' abilities to probe
the microcosm. The uncertainty principle is more than just an irreducible
fuzziness existing "out there." It seems to be tightly bound up with the
process of measurement. There's no attribute, for instance, that is intrinsi-

cally uncertain; any attribute we please can be measured with perfect
accuracy. However, our choice of what we will precisely measure makes
conjugate attributes maximally uncertain. Quantum uncertainty is not
tied to one particular attribute but slides from attribute to attribute as we
change our minds about what to measure.

In the early days of quantum theory this measurement-dependent un-
certainty was attributed to an unavoidable disturbance of the quantum
system by measurement—a disturbance which could neither be mini-
mized (because Planck's constant enforces a minimum action exchange)
nor calculated (because of quantum randomness). However, the slippery,
shifting uncertainty of conjugate attributes is much too systematic to be
explained by simple disturbance models of quantum measurement.

A second argument against the disturbance model of measurement is
the existence of "Renninger-style measurements"—measurements in
which information is gained about a system through the absence of a
detection event. Mauritius Renninger was a German physicist who first
pointed out the possibility of gaining information by observing that "noth-
ing happens."

As an example of a Renninger-style measurement, consider a quantum
system that possesses just two possibilities—for instance, light from a dis-
tant star which can bounce off either mirror A or mirror B of a stellar
interferometer. Suppose we know that a photon is on its way to the mir-
rors but do not know which path it will take. We place a detector in path
A and it does not click. The absence of a click in path A tells us that the
photon must have taken path B. We have measured the position of a
photon without explicitly interacting with it. Renninger and others looked
closely at such null measurements and found to their surprise that they are
equivalent in every way to measurements in which something actually
happens—that is, in von Neumann's terms they "collapse the wave func-
tion" as well as increase the uncertainty of the conjugate attribute.

In the disturbance model, an electron actually possesses attributes
which are unpredictably changed by the measuring device. What goes on
in a quantum measurement is not so simple, according to the Copenhagen
school. Bohr's explanation of the slipperiness of quantum attributes is that
such attributes do not belong to the quon itself but reside in "the entire
measurement situation"—a phrase Bohr was particularly fond of. When
we measure a certain attribute, we should not imagine that the electron
actually possesses this attribute. Electrons possess no attributes of their

own. An electron's so-called attributes are really relations between the
electron and its measuring device and do not properly belong to either.

Bohr's notion of relational reality explains why an attribute's uncer-
tainty depends on the type of measurement performed and why attributes
are affected by measurements as non-disturbing as Renninger's "no-show"
techniques. Since the electron's "attributes" reside in the relation between
quon and M device, one can influence the attribute by merely changing
the device.

Support for Bohr's relational reality concept comes from the way quan-
tum theory actually works. A quantum measurement corresponds to ana-
lyzing a particular waveshape into a certain family of waveforms—tuba or
piano waves, for instance. Each waveform family represents a particular
quantum attribute. The question is, do attributes of this kind truly belong
to the quon in question or do they partly belong to the M device—to the
analyzer prism, for instance?

Record on tape a few minutes of traffic noise. If we analyzed this noise
into tuba waveforms we could say that in a certain sense traffic noise is a
chorus of tubas. But we could equally well say that it's a chorus of pianos
or saxophones. There is a sense in which noise is made of these waveforms.
However, we know that real traffic noise has no intrinsic tuba, piano, or
saxophone qualities. These musical sounds derive as much from the ana-
lyzer as they do from the noise itself.

It is the same with quantum entities, says Bohr. Electrons do not pos-
sess position, momentum, or any other dynamic attributes. These so-called
attributes are not intrinsic properties of quantum systems but manifesta-
tions of "the entire experimental situation." It makes no sense to talk
about the dynamic attributes of the electron itself. Such "attributes" only
arise in a particular measurement context and change when that context
changes. According to Bohr, "Isolated material particles are abstractions,
their properties being definable and observable only through their interac-
tion with other systems."

An obvious feature of the ordinary world is that it seems to be made of
objects. An object is an entity that presents different images from differ-
ent points of view and to different senses, but all these images can be
thought of as being produced by one central cause. No one sees (smells,
feels) the same subjective apple, but everyone agrees that there is one
objective apple that is the source of these varied sensations. Its division
into objects is a most important aspect of the everyday world. But the

situation is different in the quantum world (which is, after all, only the
ordinary world examined closely).

The separate images that we form of the quantum world (wave, parti-
cle, for example) from different experimental viewpoints do not combine
into one comprehensive whole. There is no single image that corresponds
to an electron. The quantum world is not made up of objects. As Heisen-
berg puts it, "Atoms are not things."

This does not mean that the quantum world is subjective. The quantum
world is as objective as our own: different people taking the same view-
point see the same thing, but the quantum world is not made of objects
(different viewpoints do not add up). The quantum world is objective but
objectless.

An example of a phenomenon which is objective but not an object is
the rainbow. A rainbow has no end (hence no pot of gold) because the
rainbow is not a "thing." A rainbow appears in a different place for each
observer—in fact, each of your eyes sees a slightly different rainbow. Yet
the rainbow is an objective phenomenon; it can be photographed.

For Bohr, the search for deep reality—for "real" quantum attributes
which an electron possesses independently of observation—is as misguided
as looking for the rainbow's end. An electron's attributes do not belong to
the electron itself but are a kind of illusion produced by the electron plus
"the entire experimental arrangement."

We like to think that although the rainbow is not an object, it is really
made of objects: an illusion constructed of non-illusory sunlight and rain.
Likewise we need some hard facts out of which to construct the electron's
illusory attributes. In the Copenhagen interpretation, the ultimate "hard
fact" is the measurement device itself. In an obvious way, phosphor
screens are made of electrons; the Copenhagenists contend that in a less
obvious way, electrons are also made of phosphor screens.

In the Copenhagen interpretation there is a sense in which the world is
not made of atoms but of M devices. Berkeley physicist Henry Stapp
comments on this peculiar reversed order of reality:

"Scientists of the late twenties, led by Bohr and Heisenberg, proposed a
conception of nature radically different from that of their predecessors
. . . Their theoretical structure did not extend down and anchor itself on
fundamental microscopic space-time realities. Instead it turned back and
anchored itself in the concrete sense realities that form the basis of social
life. This radical concept, called the Copenhagen interpretation, was bit-

terly challenged at first but became during the thirties the orthodox inter-
pretation of quantum theory, nominally accepted by almost all textbooks
and practical workers in the field."

Bohr treats M devices in a special way. He does not represent an M device
as a possibility wave but considers it a solid actuality. By objectifying the
M device, he can account for the "ordinariness" of quantum fact and
avoid such monstrosities as Schrodinger's live/dead cat which arise if you
believe that the same quantum rules hold for cats and electrons. Through-
out his career Bohr continued to emphasize the "classical style" of exis-
tence enjoyed by ordinary objects. For instance:

"Even when the phenomena transcend the scope of classical physical
theories, the account of the experimental arrangement and the recording
of observations must be given in plain language, suitably supplemented by
technical terminology."

Bohr recognizes here that the form of every quantum fact is identical to
the form of every prequantum fact—that is, nothing special. It's an un-
changeable fact of life that our direct experience of an electron (flash-on-a-
screen) is no more mysterious than our direct experience of cats and
rainbows.

But how can the measuring device evade the quantum rules which hold
for every entity in the world? I think that Bohr would answer this question
by saying that if the M device should become itself the object of measure-
ment, then it would certainly have to obey the quantum rules, but then M
device #2 must reside in a classical-style world.

However, we could imagine a third M device that measures device #2.
Now device # 2 must be represented by a possibility wave, and obeys the
superposition and uncertainty principles, but device #3 dwells in the
classical world. This endless procession of measuring devices measuring
one another is called "von Neumann's paradox of infinite regress." Von
Neumann's paradox results from the assumption of special non-quantum
entities—measuring devices—while at the same time we know that such
devices cannot really be special.

One of the drawbacks of the Copenhagen view is that it assigns a
privileged role to measuring devices, describing them in terms of definite
actualities, while every other entity is represented by superpositions of
possibilities. Surely the world itself is not so divided but consists of a single
reality. Another conceptual weakness of the Copenhagen interpretation is

that it regards both the M device and the measurement act as ultimately
unanalyzable. Thus, in the Copenhagen view quantum theory can explain
with great exactitude the behavior of atoms, but is powerless to cope with
the attributes of cats and apples in their roles as unscrutinized parts of
"the entire experimental situation".

Quantum Reality #2: The Copenhagen interpretation, Part II. (Reality is
created by observation.) Expanding on the Copenhagen interpretation's
special role for M devices, Quantum Reality #2 emphasizes the observ-
er's special status in a quantum world. Of quantum theory's many ele-
ments, the observer-created reality school stresses the quantum meter op-
tion—the observer's ability to intervene in reality by freely selecting which
attribute he wants to look at. In waveform language, the meter option
amounts to freedom to choose the waveform alphabet in which an entity's
proxy wave will be expressed: whether the traffic noise shall be made from
piano or tuba (or whatever) waves. By your choice of what attributes you
look for, say believers in observer-created reality, you choose what attri-
butes a system will seem to possess.

Professor John Archibald Wheeler has built the Institute of Theoretical
Physics at Austin, Texas, into the world's most important center for quan-
tum reality research—a sort of second Copenhagen in the Lone Star state.
Wheeler has at various times championed several different quantum reali-
ties, but none so consistently as observer-created reality. "No elementary
phenomenon is a real phenomenon until it is an observed phenomenon,"
Wheeler maintains. Perhaps this quantum reality should be called the
"Austin interpretation of quantum theory" in honor of Wheeler's insti-
tute.

If one accepts that common phenomena like the rainbow are observer-
created, one should not be so surprised by such claims made on the elec-
tron's behalf. An electron after all is surely stranger than a rainbow.
Wheeler takes observer-created reality a step beyond rainbows with what
he calls a "delayed-choice experiment." In such an experiment, the ob-
server creates not only present attributes of quantum entities, but also
attributes that such entities possessed far back in the past, which by con-
ventional thinking existed long before the experiment was conceived, let
alone carried out. The concept of a delayed-choice experiment is best
illustrated by one of Wheeler's thought experiments: the gravity-lens in-
terferometer. According to Einstein, gravity is a curvature in space-time
which shows up, for instance, in the deflection of starlight grazing the sun.

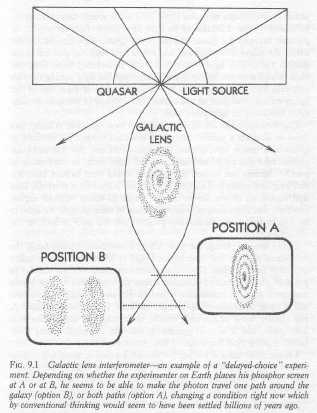
The more massive an object, the more it bends space-time, consequently
the more it deflects a beam of light. Since a typical galaxy contains some
hundred billion suns, its ability to bend light is appreciable.

A quasar is an intense source of light of controversial origin which
ignited shortly after the universe began. Recently astronomers have de-

tected double images of quasar QSO 0957+561 which they calculate to
be caused by the deflection of its light by a galaxy that happens to lie
precisely between the quasar and the Earth. Quasar light traveling to the
left of the galaxy is bent around and meets light that has traveled to the
galaxy's right. This light comes to a focus (sometimes more than one
focus, which accounts for the double image) just like light passing through
a camera lens. In this case the lens is formed, not of glass, but of the
galaxy-induced curvature of space-time. The aperture of this galactic cam-
era is thousands of light years wide.

Gravitational lenses are interesting in their own right, but Wheeler uses
them to illustrate a peculiar feature of quantum theory. We can look at
galaxy-bent quasar light photon by photon and ask, did this particular
photon take the right-hand path, the left-hand path, or both paths at
once? Whatever the answer, this question would seem to have been set-
tled long ago: we are looking here at light that is ten billion years old, light
that started on its way before our sun began to shine. Wheeler argues,
however, that depending on what we choose to measure now, we seem to
be able to influence whether this photon took one path or both in the
distant past.

Here's how to change the past. Using conventional optics, bring the
two beams together that have traveled right or left of the focusing galaxy
and allow them to cross. Now decide (quantum meter option) whether to
put your photon-sensitive phosphor screen at intersection A or at a later
position B after the beams have separated. For each photon, you can take
one of these measurement options but not both. If you choose position A,
you observe wave interference effects, indicating that the photon took
both paths, and it is even possible to estimate the relative time delay
between paths from the shape of this interference pattern.

On the other hand, if you put the phosphor screen at location B you see
that each photon takes only one path, either left or right of the galactic
lens. In our imagination we can picture this particular photon traveling
partnerless for eons, because today we chose to do experiment B instead of
experiment A. You can make the next photon take both paths by quickly
choosing the other measurement option. By our choice of what we look at
today we seem to be able to change a photon's attribute acquired billions
of years before we were born.

Wheeler's delayed-choice experiment seems to show that the past is not
fixed but alters according to present decisions. Popular philosopher Alan
Watts reports that certain Eastern philosophies have come to a similar

conclusion concerning the creative power of the present tense: "The mo-
ment of the world's creation is seen to lie, not in some unthinkably remote
past, but in the eternal now."

Note that our ability to change the past is limited. We can indeed
choose whether each quantum entity becomes a one-path or a two-path
photon, but we cannot select where the two-path photon will fall in the
interference pattern or which path the one-path photon will take. Such
details are completely outside anyone's control or prediction: we call them
"quantum random." Observer-created realities based on the meter option
(observer creation of the first kind) can select the type of attribute a quon
shall possess but not its particular attribute value.

The attributes of photons and electrons may well be observer-created,
but what about the attributes of oranges and apples? Some adherents to
observer-created reality, invoking arguments similar to Schrodinger's on
behalf of his cat, believe that only quantum entities such as electrons and
photons possess observer-malleable attributes. Wheeler, for instance,
stresses that only elementary phenomena are unreal until observed. Pre-
sumably the attributes of non-elementary phenomena such as cats and
apples are real whether we look at them or not. However, it is difficult to
draw a sharp line between classical and quantum entities. Other physicists
of OCR persuasion draw no such line: for instance, Cornell's N. David
Mermin believes that the attributes of all entities—cats, oranges, rain-
bows, even the moon and stars—are not real until somebody looks at them
under the auspices of a particular meter option.

In addition to differing over which entities can benefit from an observa-
tion, partisans of an observer-created reality do not agree on what counts
as an observation. Quantum theory itself does not say what is or is not a
measurement but tells us that if we can find out how to make a measure-
ment, it will predict the results. Luckily we already knew how to make
measurements before the advent of quantum theory.

Wheeler and many of his colleagues have concluded that the essence of
measurement is the making of a record. In their opinion, a Geiger counter
or Polaroid (self-developing) film is competent to act as observer, assigning
attributes via the meter option to observed entities now and forever after-
ward in the past.

A few physicists believe that record-making machines are not enough:
only a conscious observation counts as a measurement (observer-creation
of the second kind). Until conscious observers came upon the scene, the
universe existed in an indefinite state, unable to decide even what kinds of

attributes it possessed let alone their particular values. Large portions of
the universe (everything that's not being looked at right now by a con-
scious observer) are still in this indecisive situation, waiting for a conscious
observer to grant them a more definite style of existence.

Bishop Berkeley taught that matter possessed reality only insofar as it
was perceived by some mind. No believer in observer-created reality, even
the most extreme, goes as far as Berkeley. Every physicist upholds the
absolute existence of matter—electrons, photons and the like—as well as
certain of matter's static attributes. However, observer-created reality
physicists do believe that dynamic attributes—position and momentum,
for instance—do not exist until they are actually observed. Electrons cer-
tainly exist—with the same mass and charge whether you look or not—
but it is a mistake to imagine them in particular locations or traveling in a
particular direction unless you actually happen to see one doing so.

Quantum Reality #3: Reality is an undivided wholeness. The contention
of David Bohm and others that despite its obvious separations the world is
a seamless whole is related to Bohr's notion that quantum attributes are
not localized in the quon itself but reside (like the position attribute of a
rainbow) in "the entire experimental arrangement." Certain features of
quantum theory imply that this innocent expression "entire experimental
arrangement" may have to include not only activities in the immediate
vicinity of the quon's actual detector but actions arbitrarily remote in time
and space from the detection site. Ultimately the whole universe may be
implicated in a simple measurement, in the selection of a single quon's
observed attributes.

The basis for this claim of undivided wholeness is rooted in a curious
feature of quantum theory called "phase entanglement." All previously
mentioned puzzles of quantum theory concerned the process in which a
single quon acquires its attributes. The concept of "phase entanglement"
arises when we consider how two or more interacting quons acquire their
attributes.

Whenever two quons meet, so do their representative proxy waves.
Their time together is represented by a merging of proxy waves. The
separation of these quons is represented by a separation of proxy-wave
amplitudes, but the phases of the two quons do not come apart. Instead
these phases become entangled in such a way that interference effects at
quon A depend instantaneously on the disposition of quon B.

The reason that quantum waves become phrase-entangled and ordinary

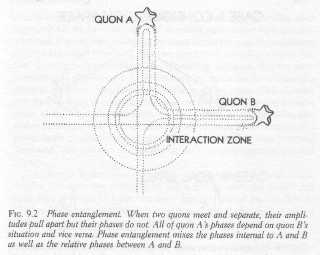
waves don't is that quantum waves do not make their home in ordinary
three-dimensional space but in a place called configuration space. The
difference between a couple of waves in ordinary space and in configura-
tion space is illustrated in Fig. 9.3. For simplicity we imagine both waves
to be one-dimensional, like waves on a string. In ordinary space we see two
waves, A and B, traveling on the same one-dimensional string. The same
situation represented in configuration space looks like one wave in two
dimensions: waves A and B are not separate but different aspects of a
single waveshape.

Configuration space consists of three dimensions for each quon. Thus
the proxy wave for the two-quon hydrogen atom (electron plus proton)
resides in a space of six dimensions. The main reason that physicists con-
sider the wave function to be fictitious is that it moves around in a space
with many more dimensions than our own.

A disturbing feature of phase-entangled quons, first emphasized by Er-
win Schrodinger, is the strange action-at-a-distance such entangled sys-
tems seem to possess—at least on paper. Because of their phase-connect-
edness (or alternatively because they are represented by a single wave in

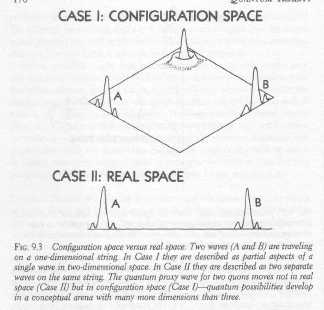
multidimensional space) an action on quon A seems to have an instanta-
neous effect on the wave function of quon B even when the two quons are
no longer capable of interacting via conventional forces. Schrodinger
found this apparent instant connection so unusual that he called it not one
but the chief feature of quantum theory.

However, the fact that such a tight connection between separated
quons exists in the formalism of quantum theory is no guarantee that such
a connection exists in reality. Quantum connectedness may be as fictitious
as the dotted lines that outline the constellations in star maps. Despite the
fact that "something" seems to be linking two quons instantly (faster than
light), quantum theory does not seem to permit any messages to be sent
along this link (see Eberhard's proof in Chapter 13), a fact which height-
ens the impression that such links are spurious.

The fact that observing a quon here instantly changes the wave func-

tion there (where "there" may be billions of miles away) is another good
argument for the fictitious nature of the proxy wave. If the wave function
were real, it would have to change its shape drastically over large distances
at faster-than-light speeds. As far as we know, nothing real can move that
fast. To cope with such objections, Heisenberg suggested that the wave
function does not represent a real situation but rather our knowledge of a
physical situation. Wave function collapse is not an actual physical event
but represents the change that occurs in our knowledge when we become
aware of the result of a measurement. The knowledge interpretation also
makes Renninger-style measurements (in which no actual detections take
place) easier to understand: in certain situations the fact that "nothing
happened" can increase our knowledge with no accompanying physical
change.

If a friend in Texas seals a silver coin in one envelope and a gold coin in
another and mails the envelopes to Tokyo and London, the instant you
open your envelope in Japan you know the contents of my envelope in
England. But opening your letter causes no physical change in England
(faster-than-light or otherwise) but merely involves a change in your
knowledge concerning something happening far away and outside your
control. We certainly learn something about one coin by looking at the
other. However, this knowledge is not physically transmitted from London
to Tokyo but resides in the preestablished relation between the two coins.
The silver and gold coins are correlated but not connected. No real link
exists between them. Likewise, according to Heisenberg's knowledge in-
terpretation, nothing real connects isolated far-flung phase-entangled
quons. Instantaneous phase connections exist in the mathematics but not
in the real world. You should not take them seriously.

Many entities that seem to exist are not part of the real world—for
instance, the virtual image. A virtual image appears to be someplace where
in fact it is not. A rainbow is a virtual image: it can seem to be located
where there is neither rain nor sunlight. Alice's world on the other side of
the mirror is likewise a virtual image. As far as the laws of optics are
concerned, these images are just as real as your nose. They can be photo-
graphed, magnified, and reflected just like the image of any real object.
But ordinary experience has stricter criteria for what's real and what's not
than the laws of optics. As any child knows, there's nothing at all in back
of a mirror.

On the other hand the silver/gold coin analogy, however persuasive,
may not be an appropriate model for quantum correlations. Heisenberg

did indeed suggest that the wave function collapse represented a change
in the observer's knowledge rather than a real physical event, but he was
careful to add that such knowledge was not of some preexisting reality.
Knowledge of a quantum system is not attained by passive inspection but
only by active intervention on the part of the observer. "What we learn
about," says Heisenberg, "is not nature itself, but nature exposed to our
methods of questioning."

Just as quantum ignorance is different from the classical kind, the
"knowledge" that we gain in a quantum measurement is of a different sort
from the knowledge we gain from opening an envelope. Perhaps we can-
not so easily dismiss the reality of instant connectedness by appealing to
ordinary knowledge models such as correlated coins.

This suspicion that mathematical phase entanglement is evidence for a
real world quantum connection was strengthened by John Bell's discovery
that quantum correlations are too strong to be explained by ordinary
knowledge models of the silver/gold coin variety. Bell's theorem, reviewed
in Chapter 12, shows that to account for the behavior of certain two-
photon systems, extremely drastic models of reality must be invoked, mod-
els that necessitate the real existence of a pervasive and powerful long-
range connectedness.

Quantum Reality #4: The many-worlds interpretation. This quantum
reality, first dreamed up by Hugh Everett in 1957 while a Ph.D. candidate
under John Wheeler, takes the quantum measurement problem seriously
and solves it in a bold and flamboyant manner.

The measurement problem can be expressed in many ways. Everett saw
it like this: the orthodox ontology treats measurement as a special kind of
interaction, yet we know that measurement interactions cannot really be
special since M devices are no different from anything else in the world.
How, then, asks Everett, can we strip the measurement act of its privi-
leged status and achieve within physics that democracy of interactions
which certainly prevails in nature?

Bohr, for instance, assigns special status to measuring devices, confer-
ring on them a classical-style actuality not possessed by the atomic entities
under their scrutiny. Von Neumann, on the other hand, does not consider
M devices special: he describes them in terms of possibility waves just like
atoms. However, the price von Neumann has to pay to purchase this
equality of being is the necessary elevation of the measurement act to
special status. Unlike any other interaction in nature, measurement has

the power to collapse the wave function from many parallel possibilities
(the premeasurement superposition of possibilities) to just one (the actual
measurement result).

Following von Neumann's picture of quantum theory, Everett repre-
sents everything by proxy waves, but he leaves out the wave function
collapse. When a quantum system encounters an M device set to measure
a particular attribute, it splits as usual into many waveforms, each corre-
sponding to a possible value of that attribute. What is new in Everett's
model is that correlated to every one of these system wave functions is a
different M-device waveform which records one of these attribute values.
Thus if the measured attribute has five possible values, the quantum-
entity-plus-measuring-device develops into five quantum systems, each
with a different attribute value paired with five measuring devices each
registering that value. Instead of collapsing from five possibilities to one
actual outcome, the quantum system in Everett's interpretation realizes
all five outcomes.

To account for the stubborn fact that no one has ever seen one M
device turn into five, Everett makes a not-so-modest proposal. The appara-
tus actually does split into five different parts, says Everett, but each part
occupies its own parallel universe. A human being—one of Everett's crit-
ics, for instance—dwells in just one of these universes (at a time) and
cannot perceive the other four. Likewise the inhabitants of the other four
universes are not aware of their parallel partners.

The "ordinariness" of quantum facts in spite of the real existence of
multiple universes is accounted for in Everett's model by the fact that
each human observer perceives only a single universe. We do not know
why human perception is limited to such a small sector of the real world,
but it seems to be an unavoidable fact. We are not directly aware of these
alternate worlds, but our own universe would not be the same without
them.

Everett's quantum theory without collapse describes the world as a
continually proliferating jungle of conflicting possibilities, each isolated
inside its own universe. In that world (which we might call super reality)
one M device splits into five. However, humans do not happen to live in
super reality but in the world of mere reality, where only one thing hap-
pens at a time. We can picture Everett's super reality as a continually
branching tree of possibilities in which everything that can happen actu-
ally does happen. Each individual's experience (lived out in mere reality,

not super reality) is a tiny portion of a single branch on that lush and
perpetually flowering tree.

All interactions in Everett's super-real world are of the same kind: two
systems come together, get correlated, then start to realize all their mutual
possibilities. A measuring device is just like any other quantum entity
except that its macroscopic attributes happen to be especially sensitive to
some attribute (usually position) of an atomic entity with which it may
become correlated. Lots of entities become correlated with photons, but
few qualify as photon detectors because their visible attributes are not
significantly changed by this photonic association. Our phosphor/screen
combination is different: it prints a mark on a tape whenever it correlates
with a photon's position attribute. In Everett's model, M devices are not
essentially different from anything else except in certain unimportant de-
tails.

Everett's many-worlds interpretation of quantum theory, despite its ex-
travagant assumption of numerous unobservable parallel worlds, is a favor-
ite model of many theoretical physicists because of all quantum realities it
alone seems to solve the measurement problem with no arbitrary canoniza-
tion of the process of measurement. In Everett's picture all measurement
devices and measurement acts are fundamentally of the same nature as all
other devices and acts. Strictly speaking, there are no "measurements" in
the world, only correlations.

Einstein objected to suggestions of observer-created reality in quantum
theory by saying that he could not imagine that a mouse could change the
universe drastically simply by looking at it. Everett answers Einstein's
objection by saying that the actual situation is quite the other way around.
"It is not so much the system," Everett says, "which is affected by an
observation, as the observer who becomes correlated to the system." The
moral of Everett's tale is plain: if you don't want to split, stop looking at
attribute-laden systems.

At a recent conference on the nature of quantum reality, Berkeley
physicist Henry Stapp suggested an advantage that Everett's quantum
reality confers on biological evolution and similar improbable but not
impossible processes. Suppose, says Stapp, you could calculate the odds for
life to begin on Earth and found them to be infinitesimally small but not
actually zero. In the conventional single-universe model of things, some-
thing with a very small probability is effectively impossible: it will never

happen. However, in the Everett picture everything that can happen does
happen. If life on Earth is possible at all, then it is inevitable—in some
corner of super reality. In Everett's bountiful multiverse, every little
could be," no matter how improbable, gets its time to shine.

10 -

Quantum Realities: Four More

"I want to know how God created this world. I am not interested in
this or that phenomenon, in the spectrum of this or that element. I
want to know His thoughts, the rest are details."

---Albert Einstein

Quantum Reality #5: Quantum logic. (The world obeys a non-human
kind of reasoning.) In 1936 John von Neumann and Harvard mathemati-
cian Garrett Birkhoff proposed a new approach to quantum theory which
they called quantum logic. An entity's "logic" means how its attributes
combine to make new attributes.

The attributes of classical objects follow a familiar pattern called
Boolean logic after George Boole, an Irish schoolteacher who first codified
the structure of ordinary reasoning. Birkhoff and von Neumann show that
because quantum attributes are represented by waveforms, they combine
according to a peculiar "wave logic."

Consider a collection of entities that can possess attributes A or B or
both. From the set of entities all of which possess attribute A and the set

all of which possess attribute B we can form two new sets by combining
sets A and B according to the logical operations and and or.

When we combine sets A and B according to the and operation we get
another set C (symbolically A and B = C) which contains all entities
possessing both attribute A and attribute B. The joint possession of both
attributes may be regarded as a new attribute, attribute C. Note that A
and A = A.

Combining sets A and B according to the or operation, we get another
set D (symbolically A or B = D) which contains all entities possessing
either attribute A or attribute B or both. The possession of either of these
attributes can be regarded as a new attribute, attribute D. Note that A or
A = A.

Logic Lattices

To picture the structure of various logics, mathematicians use a diagram
called a lattice which shows at a glance all and/or relations between
attributes. A lattice orders a system's attributes according to their inclu-
siveness, with the most inclusive attribute on top. Attributes are con-
nected by lines that show how each pair of lower attributes are connected
by lines that show how each pair of lower attributes joins together to form
a higher attribute. An example of a classical logic lattice is the color lattice
which lays out the logical relations that exist among the primary and
process colors (Fig. 10.1). Primary colors (red, green, blue) are the basis of
additive color mixtures such as those which create full-color TV images.
Color printing (subtractive color process) is based on mixtures of the pro-
cess colors yellow, magenta, and cyan.

To compute the result of the and operation on any pair of attributes A
and B from a lattice diagram, find the highest common attribute that can
be reached by following lines downward from A and from B. For instance,
the operation (cyan and magenta) is calculated by following lattice lines
down from the cyan and magenta attributes. The highest attribute which
these downward lines intersect is blue. We say that cyan and magenta =
blue which means that blue is the most inclusive attribute that cyan and
magenta have in common. In like manner one can read off from the
lattice the result of the and operation applied to any pair of attributes.

To calculate the result of the OR operation on any pair of attributes A
and B from a lattice diagram, find the lowest common attribute that can be

reached by following lines upward from A and from B. For instance, the
operation (cyan or magenta) is calculated by following lattice lines up
from the cyan and magenta attributes. The lowest attribute which these
upward lines intersect is white. The white attribute is labeled "All" in Fig.
10.1 because white light is a mixture of all colors. We say that cyan or
magenta == white, which means that white is the smallest (least inclusive)
attribute containing both cyan and magenta.

These and/or relations are more than abstract logical connections;
they correspond to actual physical operations. The and operation is car-
ried out by putting together color filters. The operation cyan and ma-
genta = blue corresponds to putting a cyan filter (which passes only cyan
light) together with a magenta filter (which passes only magenta light) to
make a combination filter which passes only blue light.

Just as the and operation corresponds to putting together two colored
filters, so the or operation corresponds to mixing together two colored
lights. The operation cyan or magenta = white describes the production
of "white" light by mixing cyan and magenta lights. Since magenta and
cyan both contain blue, the combination light is not pure white but blu-
ish; nonetheless the light is still called "white" because a white-light de-
tector (orthochromatic film or broad-band phosphor) will respond to such
light over its entire range of sensitivity.

Color is a classical attribute which follows Boole's rules for and and or;
the color lattice is an example of a Boolean lattice. A simple example of a

not hold for this particular combination of attributes. Other examples can
easily be found. The polarization attributes P(0) and P(45) form a non-
distributive lattice. However, even though the polarization lattice violates
one of the Boolean rules, it can always be divided into sublattices which
are entirely Boolean. For example, the four-element sublattice consisting
of attributes (H, V, N, A) and the sublattice consisting of (S, D, N, A) are
both Boolean but the total lattice is not.

All of a classical object's attributes can be measured simultaneously: a
classical object is completely open to view. A quantum entity is different:
only a certain set of compatible attributes can be simultaneously measured.
The Boolean sublattices of the full quantum logic lattice consist only of
compatible attributes (H and V, for instance) that can be measured simul-
taneously. Compatible attributes follow ordinary logic—a logic which re-
flects the "surface ordinariness" of quantum fact—the human condition
repeatedly stressed by Bohr that everything we experience in this world
must be describable in "classical"—that is, Boolean language.

A quantum entity is never completely open to view: its visible compati-
ble attributes represent only part of its full range of possibilities. The rest
of the quantum lattice contains those hidden relationships which distin-
guish a quantum entity from a classical object. All quantum lattices consist
of a union of Boolean sublattices (which some call the "isles of Boole")
adrift in a wave-logical ocean of non-Boolean relations. Within each isle of
Boole, normal logical relations prevail, corresponding to the surface ordi-
nariness (Cinderella effect) of compatible quantum attributes. However,
relations between the Boolean isles do not satisfy the distributive law,
which suggests that for quantum entities something is fishy about the
connection between the whole and its parts.

Quantum logic has made little impact on practical physics because most
of the work carried out in its name has been concerned neither with the
nature of reality nor the elucidation of experiments but with the mathe-
matical study of non-distributive lattices for their own sake. A notable
exception to this general preoccupation with formalism at the expense of
physics is the work of Georgia Tech theorist David Finkelstein who hopes
to use quantum logic to see beyond quantum theory into the actual pro-
cesses that run the world.

Unlike Bohr, who held that quantum attributes are relational—shared
jointly between quon and M device—or Wheeler, who believes that attri-
butes are observer-created, Finkelstein takes the common-sense view that
quons actually possess their measured attributes in the manner of classical

objects. In Finkelstein's model, quons differ from classical objects not in
how they possess their attributes but in how these attributes combine to
make new attributes. Quantum entities possess classical attributes that
obey a non-classical logic.

A classical object has parts that fit together in only one way—like clock-
work which can be fully described by a parts list and an assembly drawing.
A quantum entity, on the other hand, follows "wave logic" and doesn't
have definite parts: it can break up in a great many different ways, as many
ways as there are waveform alphabets into which its proxy wave can be
analyzed. Each of these divisions yields a valid classical-style view of the
quantum entity, but the connection between these ordinary views is gov-
erned by a wave logic whose image is not an assembly drawing but a non-
distributive lattice.

The Three-polarizer Paradox

As an example of wave logic in action, consider the so-called "three-
polarizer paradox." A polarizing filter is a sheet of gray plastic that passes
only one kind of polarized light.

Like the calcite crystal, a polarizing filter has an optic axis, and splits
light into two beams—one beam polarized parallel to and one beam po-

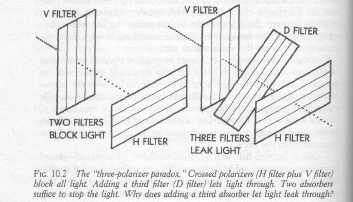
Thus although there is no V light at all in a pure H beam, such a beam
contains waveforms S and D which are each half V light: however, this V
light is entirely suppressed by destructive interference.

We now see how the absorption of an attribute can let through more
light. The insertion of the third polarizer (D filter) absorbs S light out of
the pure H beam. The removal of S light spoils the perfect destructive
interference that yielded zero V light. The D light that's left is half V
light with nothing around to cancel it. This uncanceled V light is what
gets through the second filter. Putting in an absorber lets through more
light. By removing one member of a pair of interfering attributes, the D
filter appears to create light out of nowhere.

This curious behavior of polarizing filters is complementary to the be-
havior of Sheldon Glashow's quark-mediated K-particle decay discussed in
Chapter 6. In Glashow's case the addition of a second quark channel
completely suppresses a certain type of decay because the wave nature of
the two channels permits them to cancel each other out. In the three-
polarizer paradox, taking away light lets more light through (less is more);
in Glashow's quark model of K-particle decay, adding a second decay
channel suppresses decay altogether (more is less). As these examples

show, quantum attributes do not obey the laws of ordinary arithmetic but
a peculiar kind of wave arithmetic.

Quantum logicians explain the three-polarizer paradox as a simple case
of non-distributive logic. The H filter lets through only photons that are
H-polarized. The intervening D filter lets through photons that are both
H-polarized and D-polarized. However, even though no H photon can be
V-polarized, some photons which are both H and D happen to be V-po-
larized.

A Non-boolean Roundup

The strangeness of this quantum-logical description of the three-polarizer
paradox can be appreciated by applying it to a more familiar situation. I
owe this illustration to peripatetic philosopher of science Ariadna
Chernavska.

Suppose we pass cattle through a gate which only lets through horses
and rejects all cows. Next we pass these horses through a second gate
which lets through only black animals and rejects all white ones. Only
animals which are both horses and black can pass both gates. To our
surprise, approximately half of such animals turn out to be cows!

Of course cattle don't behave this way, but if we believe the quantum
logicians that's exactly what happens to polarized photons when they go
through little sheets of plastic. A photon's attributes obey a non-human
logic which we must learn to understand if we want to make sense of
what's really going on in the quantum world.

Quantum Reality #6: Neorealism. (The world is made of ordinary ob-
jects.) The bottom line of many quantum experiments consists of a pat-
tern of tiny flashes on a phosphor screen. Is it so obvious that such a
simple phenomenon—the basis of all TV images—can be explained only
by resorting to some bizarre quantum reality? Watching those little flashes
of light appear on the screen one by one, it's easy to imagine that they are
actually caused by little objects—by real electrons with position and mo-
mentum attributes all their own. This common-sense notion that the ordi-
nariness of direct experience can be explained by an equally ordinary un-
derlying reality is the basis for a quantum reality I call neorealism.
Neorealists claim that the familiar objects that make up the everyday

world are themselves made of ordinary objects; they believe, in short, that
atoms are "things."

This straightforward view of the world's real nature has been generally
dismissed by establishment physicists as misguided and hopelessly naive.
Werner Heisenberg, for instance, considered this way of thinking as out-
moded as the idea of a flat Earth: "The ontology of materialism rested
upon the illusion that the kind of existence, the direct 'actuality' of the
world around us, can be extrapolated into the atomic range. This extrapo-
lation, however, is impossible . . . Atoms are not things."

Not only was neorealism rejected by Heisenberg, Bohr, and other
founding fathers of quantum theory as well as most of the scientific rank
and file, it was condemned by the New Physics' foremost mathematical
authority. World-class mathematician John von Neumann, in his quantum
bible, considered the claims of the neorealists and conclusively rejected
them. Von Neumann showed that because quantum theory represents
attributes by waveforms, it makes predictions which no collection of ordi-
nary objects can duplicate. In other words, if quantum theory is correct,
neorealism is impossible. This conclusion, known as von Neumann's proof,
strengthened the case for the prevailing Copenhagen view, considerably
dampened physicists' enthusiasm for neorealist heresies, and effectively
closed off research into object-based models of the world for more than
twenty years.

Quantum Monte

Though no one has ever seen an atom—our experience of such entities is
tantalizingly indirect—von Neumann proved that whatever atoms may be,
they cannot resemble ordinary objects. To get a feeling for how a mathe-
matician could prove anything at all about an invisible reality, consider the
following situation:

A fast-talking, flashy-dressed character on a New York street corner
offers you a chance to earn some easy money. On his folding suitcase-table
he lays out three cards face down. For a broker's fee of ten dollars he will
give you two of these cards. If the cards you choose are the same color, he
will buy them back for fifty dollars; a red and a black card are worthless.
To prove this is not just a simple card trick, once you have made your
choice he does not touch your cards but merely picks up the unchosen
card and replaces it in the deck.

Suppose you decide to play his game a few times and don't win. You
could blame that on bad luck. But after losing a dozen times, you might
get suspicious.

"Say, there's something funny about this game."

"Why do you say that, buddy?" He grins, flashing a row of gold teeth.

"Because I can prove that no cards can do what these cards are doing."

"Really? I'd be very interested in such a proof," he replies. "I've won-
dered a lot about these cards myself."

"Look, you can't be dealing out three cards the same color, or I'd
certainly get a pair. And if you deal out two cards of the same color plus
one odd card, I'd have one chance in three of drawing a pair, but in
twenty tries I haven't gotten any. I notice that nobody else gets any pairs
either. And this is the clincher: there's no other way to deal out three
cards."

"Is that a fact?"

"Sure, don't you see? If you've got three cards and only two colors, at
least two of the cards have got to have the same color. It's impossible to
deal out three cards each with different colors!"

"Okay, kid, you got me. But you hadda be smart to figure it out. Only a
guy with your kinda brains could have discovered these cards are special.
I'll tell you my secret. They ain't ordinary cards; they're quantum objects
my Uncle Johnny in New Jersey cooks up. Look, buddy, since you're in on
the trick now, tell ya what I'm gonna do. I'll sell you the rest of this deck
for the same price you paid for those cards you've got in your hand. As you
can plainly see, you can make a fortune with quantum objects."

This hypothetical game (I call it quantum monte) behaves a lot like
polarized photons. The arguments of the disappointed player follow the
same logic as von Neumann's proof. If the three cards on the gambler's
table are ordinary objects, there is no possibility for them all to be un-
matched. Yet the player never gets a pair no matter how long he plays.
Hence the cards cannot be ordinary objects.

This proof that the cards are not objects assumes that the gambler is
honest. In the case of "quantum monte" this assumption may be a bit
naive. In the case of polarized photons, we can probably assume that the
universe is not trying to fool us. As Einstein once remarked, "Nature is
clever but she is not malicious."

This card game resembles a typical quantum experiment in more ways
than one. Both quantum fact and quantum monte have the element of
chance in common and the fact that each event that happens is, in itself,

unremarkable (Cinderella effect). It's the statistical pattern, in both cases,
that gives the game away.

Another way in which this game resembles the quantum world is that,
in order to work, both must put a definite restriction on measurement. In
quantum monte you cannot peek at the third card; in a quantum experi-
ment you cannot look at the conjugate attribute. In both the card game
and in the laboratory nothing is ultimately hidden: you can choose (meter
option) to look at whatever you wish. However, every choice to look at one
aspect necessarily entails not looking at something else.

David Bohm's Ordinary-object Model of the Electron

In the early fifties David Bohm published his popular textbook Quantum
Theory, which remains even today one of the most lucid presentations of
the Copenhagen view. While at Princeton, conversations with the aging
Einstein, the most prominent agitator for a realistic world view ("Reality
is the real business of physics.") weakened considerably Bohm's faith in
Copenhagenism. He soon made these doubts more concrete by actually
constructing a model of the world in which the electron is an ordinary
object and which agrees with the predictions of quantum theory.

Bohm's model manages to evade the terms of von Neumann's proof
because although Bohm's electrons are objects—they have attributes of
their own—the electron's attributes behave in a most peculiar manner.
Suppose the cards in quantum monte actually were quantum objects in
the manner of Bohm's electrons. Three cards are laid out and they are all
black. You choose your first card and as you do, the other cards both
change their colors to red! Now when you turn over the next card, you will
not get a pair. The act of turning over one card caused the other cards to
change their colors!

In Bohm's model each electron is sensitively attuned to everything
that's going on in its environment, especially the presence of a measuring
device. As you set up your experiment, the electron "changes its colors"
depending on what you decide to measure. You register the value not just
of some passive attribute but of an attribute that is determined in part by
your own actions. The electron senses what's going on around it via a new
kind of field called the "pilot wave." Bohm's pilot wave puts the electron
in instant contact with every other particle in the universe. The instanta-
neousness of this connection prevents you from trying to "trick the elec-

tron" by making two simultaneous measurements at distant locations—in
effect turning over both cards at the same time. The electron's pilot wave
moves too fast for such tricks to work.

Since Bohm's model predicts the same results as quantum theory and
yet is made of little objects, von Neumann's proof obviously contains a
loophole: his notion of "ordinary objects" is too restrictive. Copenhagen-
ists protest that entities as outlandish as Bohm's hardly deserve to be
called "objects." An entity that can instantly change its properties in
response to a tiny change made half a universe away is no ordinary object.
Orders for such a change would have to move faster than light, which
Einstein has shown to be impossible. Although Bohm's electrons—"little
superluminal chameleons"—are a kind of object that might conceivably
underlie the quantum facts, Copenhagenists reject their existence on
other grounds—namely, 1. "objects" should not be in touch with every-
thing in the universe, and 2. especially not faster than light.

Bohm found he could explain the quantum facts with an underlying
reality consisting of objects, but the bizarre properties of such objects dash
any hope that Bohm's solution represents a return to ordinary reality.
Bohm's success in circumventing von Neumann's proof encouraged others
to construct different neorealist models of quantum reality, but all of these
models also contained Bohm's "defect"—this embarrassing instant con-
nection of each object to every other. CERN physicist John Bell, as part
of his celebrated theorem, showed that these instant connections are no
accident, but a necessary feature of any object-based model of reality and
of many other models of reality as well.

Quantum Reality #7: (Consciousness creates reality.) The first person to
suggest that quantum theory implies that reality is created by human
consciousness was not some crank on the fringes of physics but the emi-
nent mathematician John von Neumann. In his quantum bible Die
Grundlagen, the most influential book on quantum theory ever written,
von Neumann concludes that, from a strictly logical point of view, only
the presence of consciousness can solve the measurement problem. As a
professional mathematician, von Neumann was accustomed to boldly fol-
lowing a logical argument wherever it might lead. Here, however, was a
severe test for his professionalism, for his logic leads to a particularly
unpalatable conclusion: that the world is not objectively real but depends
on the mind of the observer.
Von Neumann's argument may be difficult to believe but it is easy to

understand. He begins by assuming that quantum theory is correct and
applies to everything in the world, measuring devices in particular. This
means that everything in the world is represented by a proxy wave. Bohr,
you will recall, granted M devices a special exemption from the quantum
description; in the Copenhagen interpretation, M devices enjoy a special
classical-style status. On the other hand, in von Neumann's all-quantum
model measurement devices are not special but are represented by proxy
waves like everything else.

The price von Neumann must pay for treating all entities alike is the
need for a wave function collapse. Somewhere between the system being
observed and the mind of the observer, the proxy wave, instead of ex-
panding to fill all its possibilities (the natural tendency of proxy waves
everywhere), must contract into just one possibility—the actual measure-
ment result. What's special in von Neumann's model is not the measuring
device but the measurement act, where many waves suddenly shrink into
one. Von Neumann showed that this special act—the wave function col-
lapse or "quantum jump"—could be located anywhere without changing
the final results, but it could not be eliminated. In von Neumann's all-
quantum description of the world, the quantum measurement problem
boils down to one question: where in fact does the wave function collapse?

Between the measured system itself and the observer's mind stretches a
series of intermediate devices (each represented by its own proxy wave)
called the von Neumann chain. Solving the measurement problem on von
Neumann's terms means finding the location at which nature breaks this
chain with a quantum jump.

Von Neumann's version of the measurement problem would be easily
resolved if we could just regard the wave function collapse not as an actual
physical process but as a mere artifact of the theory—a spurious detail
present in the math but not in the real world. When dice come up seven,
for instance, we do not regard this as a "collapse" of spread-out dice
possibility into one particular actuality. Why then should we regard the
quantum probability collapse as any more real than the realization of a
dice event?

The trouble with this easy solution is that the quantum ignorance
which lies behind quantum probability is different in kind from the classi-
cal ignorance responsible for dice odds. According to the orthodox ontol-
ogy, every individual quon is exactly alike until the quantum jump occurs:
hence this jump is more than an individual realization of laws that hold for

ensembles; the quantum jump is a sudden change in the rules that influ-
ence single events.

Every link in von Neumann's chain (with one exception) consists of
aggregates of quons interacting with other quons. Since all quons are
fundamentally the same, these interactions are all qualitatively alike. Out-
side a measurement situation, a quon's wave function has no tendency to
collapse. How can a collection of quons possibly know whether it's located
"in the wild" or inside some M device? In a system consisting solely of
quons, no special site seems to exist which might host a quantum leap;
there's no natural boundary line between measurer and measuree.

Some physicists have proposed that the essence of measurement is mak-
ing a record. Since making a record always involves an irreversible event—
else the record would fade—they suggest that von Neumann's chain
breaks naturally at the first thermodynamically irreversible process. How-
ever, despite much talk about how thermal disorder might hold the key to
the measurement problem, the fact remains that no one has succeeded in
showing how random activity by itself suffices to turn quantum ignorance
(where the desired information simply doesn't exist) into classical igno-
rance (where the desired information exists but is hidden).

The existence of measurements in which "nothing happens" (Ren-
ninger-style measurement), where knowledge is gained by the absence of a
detection, is also difficult to reconcile with the view that irreversible acts
cause quantum jumps. In a Renninger-style measurement, there must al-
ways be the "possibility of an irreversible act" (a detector must actually be
present in the null channel), but this detector does not click during the
actual measurement. If we take seriously the notion that irreversible acts
collapse the wave function, Renninger measurements require us to believe
that the mere possibility of an irreversible act is sufficient to bring about a
quantum jump. The fact that such "interactionless" measurements are
possible means that the wave function collapse cannot be identified with
some specific random process occurring inside a measuring device.

The only unusual link in the von Neumann chain is the link between
the observer's brain and the observer's mind. Here, where the mystery of
matter gives way to the mystery of mind, is a privileged position for the
elusive quantum jump.

The gist of von Neumann's argument is this: in order for an all-quan-
tum world to work, a special process—the quantum jump—must be pres-
ent in all measurement acts and nowhere else. But in a world made en-
tirely of quantumstuff there are no privileged processes. The only special

process that lies outside matter's monopoly is the awareness of the ob-
server.

Here's how physicists Fritz London and Edmond Bauer sum up the
case for Quantum Reality #7:

"A coupling even with a measuring device is not yet a measurement. A
measurement is achieved only when the position of the pointer has been
observed. It is precisely this increase of knowledge acquired by observation
that gives the observer the right to choose among the different compo-
nents of the mixture predicted by theory, to reject those which are not
observed, and to attribute henceforth to the object a new wave function,
that of the pure case which he has found. We note the essential role
played by the consciousness of the observer in this transition from the
mixture to the pure case. Without his effective intervention, one would
never obtain a new [psi] function . . . Thus it is not a mysterious interac-
tion between the apparatus and the [quantum] object that produces a new
[psi] for the system during measurement. It is only the consciousness of an 'I'
who can, by virtue of his observation, set up a new objectivity."

Consciousness-created reality (QR #7) should not be confused with
mere observer-created reality (QR #2). Quantum realists belonging to
these schools make very different claims. Any observer—conscious or not
—has to make a choice of what attributes to measure (quantum meter
option), which determines into which waveforms the quantum system will
be analyzed. By his choice of what to measure, the observer will cause the
quon to take on position rather than momentum attributes, but he does
not decide what the value of this quon's position shall be. The quantum
meter option can just as well be exercised by an inanimate computer as by
a human observer. The observer "creates reality" here by choosing what
kinds of attributes a quon shall possess. (Observer creation of the first
kind.)

Consciousness-created reality goes one step farther. Consciousness
selects (or at least acts as the site for such a selection) which one of the
many position possibilities actually becomes realized. Thus the meter op-
tion selects what game shall be played (position instead of momentum, for
instance); consciousness actually deals out the cards (this particular value
of position). Consciousness "creates reality" by deciding what particular
attribute value shall materialize. (Observer creation of the second kind.)

According to Quantum Reality # 7, dynamic attributes, when not be-
ing observed, exist as a wavewise superposition of possibilities; the universe

acquires definite values for these attributes only during a conscious obser-
vation. A mere machine can't manufacture reality, in this view, unless it
embodies some kind of awareness analogous to our own; the measurement
problem is solved by a ghost in the machine. This quantum reality sug-
gests that most of the universe most of the time dwells in a half-real limbo
of possibility waiting for a conscious observer to make it fully real.

During the eighteenth century the growing success of Newton's clock-
work mechanics inclined many philosophers to the belief that all phenom-
ena, including life, mind, and spirit could ultimately be explained as types
of complex machinery. George Berkeley, bishop of Cloyne in southern
Ireland, outraged by scientific materialism, opposed it with strong philo-
sophical opinions of his own. Berkeley argued that mind is not a form of
matter but quite the opposite: matter does not even exist except as the
perception of some mind. Absolute existence belongs to minds alone—the
mind of God, the minds of humans and other spiritual beings. All other
forms of being, including matter, light, the Earth, and stars, exist only by
virtue of some mind's being aware of them. In Berkeley's philosophy—
dubbed "idealism" because it emphasizes the primacy of ideas over things
—nothing exists unless it is either a mind itself, or is perceived by a mind.
Esse est percipi (To be is to be perceived) was the Irish bishop's motto
concerning matter: "All those bodies which compose the mighty frame of
the world have no subsistence without a mind."

Quantum idealism does not go as far as Berkeley's. According to Quan-
tum Reality #7, all quons and their static attributes enjoy an absolute
existence whether they are observed or not. Only a quon's dynamic attri-
butes, including the major external attributes position and momentum,
are mind-created. Thus all those entities "which compose the mighty
frame of the world" do certainly exist without the intervention of mind,
but until someone actually looks at them, these entities possess no definite
place or motion. The peculiar existential status of unobserved quons is the
topic of my eighth quantum reality.

Quantum Reality #8: The duplex world of Werner Heisenberg. No mat-
ter how bizarre the visions of quantum realities dancing in their heads,
most physicists agree that the results of measurements are truly real. Like
ordinary people (but unlike some philosophers), physicists cannot deny the
evidence of their senses. The indubitable reality of measurement results is
a solid rock on which to found an empirical science, or from which to
launch speculative voyages into deep reality.

In most quantum realities the measurement act does not passively re-
veal some preexisting attributes of quantum entities, but actively trans-
forms "what's really there" into some form compatible with ordinary ex-
perience. One of the main quantum facts of life is that we radically
change whatever we observe. Legendary King Midas never knew the feel
of silk or a human hand after everything he touched turned to gold.
Humans are stuck in a similar Midas-like predicament: we can't directly
experience the true texture of reality because everything we touch turns to
matter.

Many of the previous quantum realities have focused on what extra
feature makes an ordinary interaction into a measurement (macroscopic
device, record-making observer, conscious spectator, for example), but lit-
tle has been said about the character of the unmeasured state. Since most
of reality most of the time dwells in this unmeasured condition, which
quantum theory represents by an uncollapsed superposition of possibilities,
the lack of such a description leaves the majority of the universe (every-
thing that's not currently being measured) shrouded in mystery.

Werner Heisenberg was one of the few physicists who attempted to
describe in non-mathematical terms the "world-in-itself," that innocent
existence quantum entities enjoy before undergoing a measurement. Hei-
senberg's description is no full-fledged model of reality, but just one man's
attempt to convey in ordinary language the flavor of the deep reality
symbolized by a [psi] wave.

Heisenberg was acutely aware of the difficulty of trying to describe the
quantum world in words. "The problems of language here are really seri-
ous," he admits. "We wish to speak in some way about the structure of the
atoms and not only about the 'facts'—for instance, the water droplets in a
cloud chamber. But we cannot speak about the atoms in ordinary lan-
guage." Heisenberg however did not let this difficulty render him speech-
less. He realized that some words are better than others for describing the
unmeasured world.

Quantum theory according to the Copenhagen interpretation repre-
sents the world in two different ways: the observer's experience is ex-
pressed in the classical language of actualities, while the unmeasured quan-
tum realm is represented as a wavewise superposition of possibilities.
Heisenberg suggests that we take these representations literally as a model
for the way things really are.

Thus, according to Heisenberg's duplex vision, the unmeasured world
actually is what quantum theory represents it to be: a superposition of

mere possibilities (Heisenberg called them potentia, unrealized tenden-
cies for action, awaiting the magic moment of measurement that will
grant one of these tendencies a more concrete style of being which we
humans experience as actuality.

Just as traffic noise contains no tubas or pianos but might be wave-
analyzed in terms of tuba or piano waveforms, so also is it a mistake to
imagine Heisenberg's world of potentia as consisting of definite preexist-
ing possibilities for certain courses of action. Superposition is not like that.
The possibilities latent in a particular proxy wave emerge only in a definite
measurement context. Not until the observer exercises his quantum meter
option can he speak of a superposition of definite possibilities. Heisen-
berg's world of potentia is not only empty of actualities, even its possibili-
ties are not as well defined, in the absence of a measurement situation, as,
say, classical dice possibilities.

Heisenberg's potentia represents a novel kind of physical existence
standing "halfway between the idea of the event and the actual event
itself." Until it's actually observed, a quantum entity must be considered
"less real" than the same entity observed. On the other hand, an unob-
served quantum entity possesses "more reality" than that available to ordi-
nary objects because it can entertain in potentia a multitude of contradic-
tory attributes which would be impossible for any fully actualized entity.
"In the experiments about atomic events we have to do with things and
facts, with phenomena that are just as real as any phenomena in daily
life," says Heisenberg. "But the atoms or the elementary particles them-
selves are not as real; they form a world of potentialities or possibilities
rather than one of things or facts."

Heisenberg's half-real universe of potentia is reminiscent of certain ori-
ental views developed in contexts far removed from quantum physics:

This floating world is but a phantasm
It is a momentary smoke

Though ghostly and transitory, Heisenberg's shimmering ocean of poten-
tia is the sole support for everything we see around us. The entire visible
universe, what Bishop Berkeley called "the mighty frame of the world,"
rests ultimately on a strange quantum kind of being no more substantial
than a promise.

Quantum Reality Reprise

Most physicists use quantum theory as mere recipe for calculating results
and don't trouble themselves about "reality." However, it is hard to be-
lieve that this theory could be so successful without corresponding in some
way to the way things really are. Like the story of the blind man and the
elephant in which each man imagines a different animal according to
which part he's holding, these eight quantum realities result from different
physicists each taking a part of quantum theory seriously and identifying it
with the "real reality" behind appearances.

Bohr, for instance, took the uncertainty principle seriously, using it to
argue that quons possess no dynamic attributes of their own. A quon's so-
called attributes reside in the relation between the entity itself and a
"classical" measuring device.

Believers in observer-created reality take the quantum meter option seri-
ously: exercising this powerful option, the observer decides which kinds of
attributes quantum entities will seem to possess.

Quantum Reality # 3 (undivided wholeness) takes phase entanglement
seriously as a token of a real physical connectedness (the quantum connec-
tion) that instantly joins each quon to every other.

Everett in his many-worlds interpretation takes the quantum measure-
ment problem seriously: he solves this problem by declaring that the wave
function collapse is an illusion caused by human inability to experience
reality fully: we are unaccountably blind to all but a single branch of a
luxuriant tree of coexistent universes.

Quantum logicians (QR # 5) view incompatible attributes as the central
quantum fact: a new form of reasoning is needed in which the strange
behavior of quantum attributes appears perfectly natural.

Neorealists (QR #6) believe that the surface ordinariness of all quan-
tum facts (Cinderella effect)—the fact that every experiment must be
described in classical language—clearly suggests that reality itself is ordi-
nary too.

Believers in consciousness-created reality take the quantum measure-
ment problem seriously and conclude that nowhere in mere quantumstuff
is there a logical site for proxy wave collapse: only the mind of the observer
can fill the bill.

Werner Heisenberg's duplex universe (QR # 8) takes literally the proxy

wave representation of quantum entities as superpositions of possibilities.
Unmeasured quantum attributes are just what quantum theory says they
are: unrealized possibilities.

Because of the Cinderella effect—the stubborn ordinariness of quan-
tum fact—we cannot experience directly any of these strange quantum
realities (with the exception of neorealism). Although these realities make
very different claims, they all predict exactly the same facts. At present
there's no way to decide experimentally among these alternative visions of
the way the world really is.

When my son asks me what the world is made of, I confidently answer
that deep down, matter is made of atoms. However, when he asks me
what atoms are like, I cannot answer though I have spent half my life
exploring this question. How dishonest I feel—as "expert" in atomic real-
ity—whenever I draw for schoolchildren the popular planetary picture of
the atom; it was known to be a lie even in their grandparents' day.

Physicists cannot explain atoms to their children, not because we are
ignorant but because we know too much. The behavior of atoms is no
longer a mystery. Quantum theorists can confidently calculate the out-
come of any conceivable atomic experiment. However, as we see, the price
physicists have paid for quantum theory's remarkable predictive power is
their inability to picture in plain language an image of the atomic world.

Thirty years after the publication of von Neumann's Die Grundlagen
(1932) the quantum reality question inspired heated debates among phi-
losophers and physicists, but little progress was made toward solving the
problem of what sort of world we actually live in. Then, in 1964, a physi-
cist named John Bell proved an important theorem which gave us a new
insight into deep reality.

11 -

The Einstein-Podolsky-
Rosen Paradox

"One can escape from this conclusion only by either assuming that
the measurement of B (telepathically) changes the real situation at
G or by denying independent real situations as such to things
which are spatially separated from each other. Both alternatives
appear to me entirely unacceptable."

---Albert Einstein

The gist of Bell's theorem is this: no local model of reality can explain the
results of a particular experiment. In short: reality is non-local. Before we
examine what "non-locality" means, let's take a look at this particular
experiment, called the EPR experiment, which is the factual basis for
Bell's important result. Like so many other innovations in twentieth-cen-
tury physics, the EPR experiment was conceived by Albert Einstein.

Although he helped put it together, Einstein was never satisfied with
quantum theory. He didn't like its intrinsic randomness ("I cannot believe
that God plays dice with the universe"), but most of all he disliked the
fact that quantum theory (as interpreted by Bohr and Heisenberg) implies
that reality is observer-created. "I cannot imagine," Einstein once said,

"that a mouse could drastically change the universe by merely looking at
it." Einstein accused Bohr and Heisenberg of attempting to restore man
(and mouse) to the center of the cosmos from which Copernicus had
ousted them nearly five hundred years ago. "The belief in an external
world independent of the perceiving subject," Einstein maintained, "is
the basis of all natural science."

Bohr responded by comparing Einstein to the critics of his own relativ-
ity theory. He pointed out that thanks to Einstein's work, physicists have
come to realize that space and time are not absolute but relative to an
observer's state of motion. In quantum theory we simply take this way of
thinking one step further and recognize that reality itself (or at least its
dynamic attributes) is also observer-dependent. Why did Einstein find it
so difficult, Bohr wondered, to accept this natural extension of his own
ideas?

"A good joke should not be repeated twice," Einstein quipped.

Niels Bohr and Albert Einstein debated the quantum reality question
for as long as they lived: Einstein failed in his attempts to assault quantum
theory head on, and reluctantly agreed with Bohr that quantum theory
describes correctly all presently conceivable experiments—a conclusion
that remains uncontested today. Einstein resorted instead to criticizing
quantum theory on the grounds that it is incomplete.

Quantum theory may be sufficient to explain experiments, Einstein
confessed, but experiments are only part of what goes on in the world.
Because quantum theory makes only statistical predictions, it cannot help
but leave out certain "elements of reality" which a more adequate theory
of the world must include.

Niels Bohr, on the other hand, claimed that although quantum theory
does give only statistical predictions, it is still complete. Quantum theory's
indefiniteness is a virtue, not a weakness, because it corresponds to an
indefiniteness that actually exists in the world. It is foolish to seek a pre-
cise description of an imprecise world; such misplaced precision is bound
to miss the mark.

Einstein put forth his best argument for quantum theory's incomplete-
ness in the form of a thought experiment involving two correlated quons.
He devised this experiment at Princeton in 1935 with the help of two
American physicists: Boris Podolsky, originally from southern Russia, and
Brooklyn-born Nathan Rosen. The original Einstein, Podolsky, and Rosen
(EPR) experiment concerned two momentum-correlated electrons, but
physicists today repeat EPR's argument using David Bohm's conceptually
simpler experiment involving two polarization-correlated photons.

Is Quantum Theory a Complete Description of Reality?

One difference between human twins and a pair of photons in the twin
state is that before conception the human twins are nonexistent, while
before measurement the photons already exist. We know that they were
emitted at a certain time from their source and are traveling with a certain
velocity toward their respective detectors.

For a pair of photons in the twin state, Einstein asked the question, "Is
the P of photon G, after it's emitted but before it's actually measured,
truly indefinite as Bohr's interpretation of quantum theory requires, or is it,
like identical twins in the womb, really definite but unknown?" In other
words, "Is our uncertainty concerning the unobserved polarizations a mat-
ter of quantum or classical ignorance?"

According to Bohr, the P of photon G does not even exist before we
measure it. G's so-called attributes belong not to the photon itself but
reside partly in "the entire experimental arrangement." Like the position
of a rainbow, polarization is a relational attribute and does not come into
existence until Green observer decides how he will deploy his apparatus at
location G (and possibly elsewhere as well). It's nonsense to suppose that
before a measurement, photon G has some definite polarization. Einstein
argues that, on the contrary, not only does photon G have a definite P in
some direction, it has a definite P in every direction.

To dramatize the difference between Bohr and Einstein, let's imagine
that Blue player moves closer to the mound so that she gets her Blue ball
before Green player gets his. Suppose she holds her bat at zero degrees
(vertically) and gets a hit, which means that her photon is V-polarized.
We now switch our camera to home plate where the spirits of Bohr and
Einstein are discussing the reality status of the as-yet-to-be measured
Green photon presently hurtling toward the Green batter at the speed of
light. To allow the great men time for debate, we imagine the usual
passage of time to be temporarily suspended.

Bohr: When I say that quantum theory is "complete," I mean that QT
says everything that can possibly be said about the reality of that Green
photon. If it's not in the theory, it's not in the photon either.

Einstein: What, then, does quantum theory say about this Green photon
now approaching the Green batter?

Bohr: In the first place, given that Blue's already measured a V photon,
coupled with the fact that this pitcher throws nothing but twin-state
photon pairs, quantum theory predicts that if Green chooses to hold his
bat vertically, he will certainly get a hit; furthermore it also predicts that if
he holds his bat horizontally, he will certainly get a miss.

Einstein: I agree with you concerning what quantum theory predicts if
Green makes either a horizontal or a vertical polarization measurement.
Now, what is supposed to happen if Green holds his bat at some other

angle?

Bohr: For Green bat angles other than zero or ninety degrees, quantum
theory gives no certain results, but only the relative probability of a hit.
For instance, if Green should hold his bat at 45 degrees, the odds are 5O-
5O that he will get a hit.

Einstein: Yes. Quantum theory indeed gives only statistical predictions
for intermediate angles. We seem to agree concerning the predictions of
the theory and about the facts of the matter—namely, that quantum
theory has never made a single incorrect prediction. We agree, as Kant
would have put it, about the appearances and about the theory. But what,
my dear Bohr, are you willing to say about the reality of this particular
Green photon magically suspended before us?

Bohr: Because I believe that quantum theory describes all physical situa-
tions completely, I must say that before it is actually measured, this pho-
ton really has a definite polarization only in the V and H directions, but
no others. To speak of a definite polarization in any other directions would
be to talk nonsense. Thus I say that, in reality, this Green photon does not
possess polarization attributes except perhaps at these exceptional angles.

Even at these special angles, for which quantum theory gives certain
results, I am not entirely convinced that these results represent a definite
attribute belonging solely to the photon. I believe that all attributes are
joint creations of photon and measuring device and do not belong to one
or the other.

Einstein: Concerning this matter of completeness ... As you know,
my friend, I cannot refute your opinion that quantum theory is a complete
theory of phenomena: it indeed seems to describe correctly the results of
every experiment my poor head has been able to imagine. But I do not
share your faith that quantum theory is a complete theory of reality. I
believe that certain elements of reality exist in the world that are not
described by the quantum formalism. In the case of this Green photon,
for example, I say that it possesses a definite polarization attribute for
every possible angle, not just for the V and H directions.

Bohr: No, my friend, you are mistaken. Except perhaps in certain special
situations where the outcome is not a matter of chance—such as the V
and H directions in this case—the photon's polarization is a joint produc-
tion of the entire experimental arrangement, and does not inhere in the
photon by itself independent of a particular measurement context.

Einstein: Forgive me, Bohr, but I have never been able to understand
your subtle reasoning in this matter. Indeed, for situations like this twin-
state baseball game, I have, with my colleagues Podolsky and Rosen, de-
vised a simple argument which convinces us that this Green photon hov-
ering in front of us possesses a definite (but unknown) polarization attri-
bute at every angle. Permit me to show you this argument.

Our reasoning depends on a certain plausible assumption, which physi-
cists nowadays call "the locality assumption": we assume that the real
factual situation of the Green photon, after it's left the source, is not
affected by how the Blue player chooses to hold her bat. In other words,
we assume that Blue's batting stance does not affect the Green photon.
This supposition seems reasonable since both photons are traveling in
opposite directions at the speed of light. Therefore one photon cannot
learn about the other's measurement situation except via signals that
travel faster than light.

Bohr: I am suspicious of this locality assumption but please continue.

Einstein: Here is our argument. For this present situation, Blue chose to
hold her bat vertically and she got a hit. But if she had held her bat at
some other angle, say 45 degrees, she would also have measured some-
thing, either a hit or a miss, we do not know which. Because this photon
pair is in the twin state we know that Green photon would be obliged to
show the same polarization that Blue got at 45 degrees. In like manner
Blue could have held her bat at any angle X and measured a certain
polarization; Green photon is compelled to have an identical polarization
at angle X.

If Green photon must have a definite polarization for each Blue mea-
surement choice, and if (by the locality assumption) Blue's measurement
choice does not physically affect the Green photon, then the Green pho-
ton must already possess a definite polarization for each angle—polariza-
tions that exist regardless of Blue's actual choice.

Thus we believe we have shown that before it strikes the Green bat, this
Green photon has already "made up its mind" as to how it will act no
matter how Green might choose to hold his bat. This Green photon must
possess a sort of hit/miss list which tells it what to do for every bat angle.
Quantum theory, on the other hand, certainly does not recognize any such
list: except for the H and V directions, it considers these results to be
"random," utterly unknown except in a probabilistic sense. Quantum the-
ory is therefore "incomplete" because it leaves out some attributes—this
hit/miss list, for example—which this photon seems to possess.

Bohr: Your argument is clever but I cannot accept your conclusion. Of
course there is no question of any mechanical influence traveling from
Blue's bat to the Green photon, but there is essentially the question of an
influence on the very conditions which define the possible types of predic-
tions regarding the future behavior of the Green light.

Einstein: Yes, I remember your making that very statement in 1935 in
response to our original EPR paper. I did not understand it then, and
despite considerable effort, I must confess that I still cannot grasp the
subtlety of your thought on this matter.

Since the author seems to have frozen our intellects, like that time-sus-
pended Green photon out there, into our ancient philosophical positions,
I will answer your old quote with two of my own which sum up my
thinking on the EPR experiment:

"We are forced (via the EPR argument) to conclude that the quantum-
mechanical description of physical reality given by wave functions is not
complete."

"One can escape from this conclusion only by either assuming that the
measurement of B (telepathically) changes the real situation at G, or by
denying independent real situations as such to things which are spatially
separated. Both alternatives appear to me entirely unacceptable."

Bohr, Einstein, and numerous other thinkers struggled with the EPR
paradox but no generally acceptable solution could be found until Bell
focused attention on the fragility of the locality assumption. Let's take a
closer look at this locality assumption so essential to the argument of
Einstein, Podolsky, and Rosen.

The Locality Assumption

The locality assumption does not mean that what happens at the Green
bat has nothing to do with what happens at the Blue bat. Since the
photons are correlated at the light source, the results at the Green and
Blue measurement sites will likewise be correlated. What locality means is
that no action on Blue's part (as she detects her Blue photon) can affect
what Green player sees (when he detects his Green photon). Locality
means that what happens at home plate is unaffected by how Blue holds
her bat at second base.

The locality assumption is necessary to EPR's argument because al-
though Blue observer could have made any polarization measurement she
pleased, she can in fact (for a single photon) make only one, because
photon polarizations at different angles are incompatible attributes.

As a homely example of EPR's reasoning, consider a shop (Enrico's
Pizza Reale) which sells three different pizzas: Sicilian, Milanese, and
Neapolitan. Whenever you order a pizza from Enrico's it arrives at your
door in ten minutes. Since a pizza takes thirty minutes to bake, you know
that the pizza you ordered must have been ready when you phoned.

Suppose you order a pizza of your choice each night (but you can only

afford one), and it's always delivered in ten minutes. Can you conclude
that Enrico keeps on hand all three kinds of pizza?

Not without a kind of locality assumption. You have to assume that
Enrico has no way of knowing what kind of pizza you are going to order
that night. If he can discover your choice beforehand, he need keep only
one pizza hot.

Your nightly freedom of choice plus the (no pizza spies) "locality as-
sumption" allows you to infer, on the basis of a series of one-pizza observa-
tions, that Enrico in reality keeps all three pizzas ready to go each night.
The argument for preexisting polarizations is the same as for preexisting
pizzas. Blue player's freedom to choose her single P measurement plus the
locality assumption allows EPR to infer that all polarizations must be
simultaneously present in the Green photon (in the form of a hit/miss
list) before Green player makes his measurement.

Hence, in the twin state, photon G already secretly knows how it will
respond to any polarization measurement that Green player might care to
make upon it. According to EPR's argument, Green photon's polarization
attribute is not indefinite at all. Green photon's hit/miss list specifies its
polarization at all measurement angles.

Bohr asserts that photon G, before it's measured, is in an indefinite
state of polarization: quantum theory does not recognize any such hit/
miss list. But Einstein, Podolsky, and Rosen can prove that such a list
exists in nature. Hence according to EPR, quantum theory is necessarily
incomplete.

It is important to realize what EPR did not do: Einstein, Podolsky, and
Rosen did not find an experimental situation where quantum theory is
factually wrong. What EPR discovered was a simple logical argument
(based on the experimental fact of perfect polarization correlation in a
certain two-photon system) that indirectly demonstrates the existence of
photon attributes which quantum theory fails to take into account. EPR
then ask, "If quantum theory is a complete theory of reality, why does it
omit these attributes?"

What's at stake here is not whether quantum theory is a complete
theory of phenomena (accounting correctly for all presently conceivable
measurements) but whether it is a complete theory of reality (accounting
correctly for whatever exists whether measurable or not). Many "refuta-
tions" of the EPR argument consist merely of demonstrating that quan-
tum theory describes correctly all twin-state polarization measurements.
EPR do not contest quantum theory's competence to describe phenom-

ena; Einstein, Podolsky, and Rosen claim, however, to have demonstrated
the existence of certain "elements of reality" (in Einstein's words), parts
of the world not directly observable which quantum theory simply leaves
out.

The EPR proof gives those who believe that what's real is only what can
be observed an opportunity to put their convictions to the test. For such
no-nonsense realists, the argument of EPR which purports to demonstrate
the existence of an extra-observational reality must be mistaken. However,
even those convinced beforehand of EPR's error found it surprisingly
difficult to point out the fallacy in their reasoning. Hundreds of papers
were published on the "EPR paradox." For thirty years physicists and
philosophers beat their heads against this proof without either refuting
EPR's logic or shedding further light on EPR's alleged "elements of real-
ity."

In 1964 the long-standing EPR stalemate was broken by the efforts of
theorist John Bell.

12 -

Bell's Interconnededness
Theorem

"Contagious magic is based upon the assumption that substances
which were once joined together possess a continuing linkage; thus
an act carried out upon a smaller unit will affect the larger unit
even though they are physically separated."

---Sir James Frazer

John Stewart Bell was born and grew up in Belfast, Northern Ireland. He
is now a theoretical physicist at CERN (a large accelerator center in
Geneva financed by Western European countries) where he specializes in
elementary particle physics. In 1964, while on sabbatical leave from
CERN, Bell decided to investigate the quantum reality question, which
had fascinated him since his undergraduate days.

Bell began by looking at von Neumann's proof, which demonstrates the
impossibility of neorealism. According to von Neumann, the world cannot
be made of ordinary objects, which possess dynamic attributes of their
own. Bell discovered that although this proof excludes objects whose attri-
butes combine in "reasonable ways," it does not forbid objects which can

change their attributes in response to their environment. This loophole in
von Neumann's proof is what allows Bohm, de Broglie, and other neoreal-
ists to build explicit ordinary-object-based models of quantum reality: all
these models contain objects whose attributes are context-sensitive.

While preparing a review article on von Neumann's proof, Bell became
interested in impossibility proofs in general and wondered whether a proof
could be constructed which would conclusively exclude any model of real-
ity that possessed certain physical characteristics. Bell himself managed to
devise such a proof which rejects all models of reality possessing the prop-
erty of "locality." This proof has since become known as Bell's theorem. It
asserts that no local model of reality can underlie the quantum facts. Bell's
theorem says that reality must be non-local.

In a letter to the author, John Bell recalls his discovery: "I had for long
been fascinated by EPR. Was there a paradox or not? I was deeply im-
pressed by Einstein's reservations about quantum mechanics and his views
of it as an incomplete theory. For several reasons the time was ripe for me
to tackle the problem head on. The result was the reverse of what I had
hoped. But I was delighted—in a region of wooliness and obscurity to
have come upon something hard and clear."

The structure of Bell's proof is as follows. For a certain class of two-
quon experiments (the EPR experiment and its variations), Bell assumes
that a local reality exists. With a bit of arithmetic he shows that this
locality assumption leads directly to a certain inequality (Bell's inequality)
which the experimental results must satisfy. Whenever these experiments
are done, they violate Bell's inequality. Hence the local-reality assumption
is mistaken. Conclusion: any reality that underlies the EPR experiment
must be non-local.

What Is a Local Interaction?

The essence of a local interaction is direct contact—as basic as a punch in
the nose. Body A affects body B locally when it either touches B or
touches something else that touches B. A gear train is a typical local
mechanism. Motion passes from one gear wheel to another in an unbro-
ken chain. Break the chain by taking out a single gear and the movement
cannot continue. Without something there to mediate it, a local interac-
tion cannot cross a gap.
On the other hand, the essence of non-locality is unmediated action-at-

a-distance. A non-local interaction jumps from body A to body B without
touching anything in between. Voodoo injury is an example of a non-local
interaction. When a voodoo practitioner sticks a pin in her doll, the dis-
tant target is (supposedly) instantly wounded, although nothing actually
travels from doll to victim. Believers in voodoo claim that an action here
causes an effect there; that's all there is to it. Without benefit of media-
tion, a non-local interaction effortlessly flashes across the void.

The unruly nature of unmediated action has moved physicists from
Galileo to Gell-Mann to unanimously reject non-local interactions as a
basis for explaining what goes on in the world. No one has so vehemently
expressed physicists' distaste for non-local interactions as Sir Isaac New-
ton:

"That one body may act upon another at a distance through a vacuum
without the mediation of anything else ... is to me so great an absur-
dity, that I believe no man, who has in philosophical matters a competent
faculty for thinking, can ever fall into."

Given his antipathy for non-local forces, Newton was somewhat embar-
rassed by his own theory of gravity. If a non-local force is "so great an
absurdity," how does the sun's gravity manage to cross millions of miles of
empty space to hold the Earth in its orbit? Concerning the actual nature
of gravity, Newton wisely held his tongue. "Hypotheses non fingo," he
declared. "I frame no hypotheses."

Newton's faith in strictly local forces was vindicated by his successors,
who explained gravity in terms of the field concept. The space between
the sun and Earth is not empty, today's physicists say: it's filled with a
gravitational field which exerts a force on any body it touches. The mod-
ern field concept allows us to regard gravity as a strictly local interaction
even though it acts across vast reaches of space. The sun's mass produces a
gravity field; this field pulls on the Earth and mediates the sun-Earth
interaction.

Physicists today share Newton's belief that the world is tied together by
strictly local connections. All presently known interactions can be ex-
plained in terms of only four fundamental forces (strong, weak, electro-
magnetic, and gravitational). In every case these forces act as if they are
mediated by fields. Since quantum theory has blurred the once sharp
distinction between particle and field (both are quantumstuff now) we can
equally well say these local forces are mediated by the exchange of parti-
cles. Thus the sun attracts the Earth (and vice versa) via the gravity field

or via an exchange of gravitons (the particle aspect of the gravity field). In
actuality gravity (as is true for the other three fundamental forces as well)
is carried neither by particle or field but by something that partakes of
both, an innately quantum go-between whose mediation makes every one
of nature's forces strictly local.

Although the concept of locality does not strictly demand it, most
forces diminish in strength as you move away from their source. It is
conceivable that a local force might stay constant or even increase with
distance from its source (the force of a stretched spring, for instance,
increases with distance). The big four forces that hold the world together
happen, however, all to decrease with distance—gravity and electromagne-
tism diminish as the inverse square; the strong and weak forces fall off
considerably faster.

The toughest limitation on a local interaction is how fast it can travel.
When you move an object A, you stretch its attached field. This field
distorts first near object A, then the field warp moves off to distant re-
gions. Einstein's special theory of relativity restricts the velocity of this
field deformation to light speed or below. According to Einstein, no mate-
rial object can travel faster than light; not even the less material field warp
can travel so fast.

Non-local influences, if they existed, would not be mediated by fields or
by anything else. When A connects to B non-locally, nothing crosses the
intervening space, hence no amount of interposed matter can shield this
interaction.

Non-local influences do not diminish with distance. They are as potent
at a million miles as at a millimeter.

Non-local influences act instantaneously. The speed of their transmis-
sion is not limited by the velocity of light.

A non-local interaction links up one location with another without
crossing space, without decay, and without delay. A non-local interaction
is, in short, unmediated, unmitigated, and immediate.

Despite physicists' traditional rejection of non-local interactions, de-
spite the fact that all known forces are incontestably local, despite Ein-
stein's prohibition against superluminal connections, and despite the fact
that no experiment has ever shown a single case of unmediated faster-
than-light communication, Bell maintains that the world is filled with
innumerable non-local influences. Furthermore these unmediated connec-
tions are present not only in rare and exotic circumstances, but underlie all

the events of everyday life. Non-local connections are ubiquitous because
reality itself is non-local.

Not all physicists believe Bell's proof to be an airtight demonstration of
the necessary existence of non-local connections. But the alternatives
these critics offer instead seem to me to be generally obscure and/or
preposterous. As we shall see in the following chapter, some physicists will
go so far as to actually "deny reality itself" rather than accept Bell's
audacious conclusion that quantum reality must be non-local.

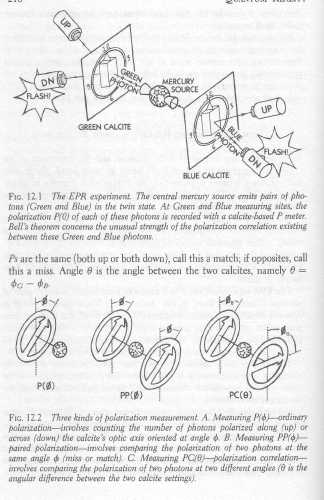
carried out this EPR experiment at Berkeley and showed that a calcite
separation of 2a degrees gives three misses for every four marks—a quite
substantial violation of the Bell inequality.

Clauser's experiment conclusively violates the Bell inequality. Hence
one of the assumptions that went into its derivation must be false. But
Bell's argument uses mainly facts that can be verified—photon PCs at
particular angles. The only assumption not experimentally accessible is the
locality assumption. Since it leads to a prediction that strongly disagrees
with experimental results, this locality assumption must be wrong. To save
the appearances, we must deny locality.

Denying locality means accepting the conclusion that when Blue ob-
server turns her calcite on Betelgeuse she instantly changes some of
Green's code on Earth. In other words, locations B and G some five
hundred light years apart are linked somehow by a non-local interaction.
This experimental refutation of the locality assumption is the factual basis
of Bell's theorem: no local reality can underlie the results of the EPR
experiment.

Einstein, Podolsky, and Rosen used the locality assumption to demon-
strate the existence of hidden "elements of reality" which quantum theory
fails to take into account. However, if Blue and Green observers are linked
by a non-local interaction, as the factual violation of the Bell inequality
seems to imply, then EPR's argument is invalid by virtue of a false prem-
ise. The failure of their argument does not prove, of course, that no such
"elements of reality" exist, but only that one cannot make a case for their
existence by using EPR's reasoning. The logical necessity of non-local
interactions resolves the EPR paradox (in Bell's words) "in the way which
Einstein would have liked the least."

Reviewing the EPR paradox in his autobiography, Einstein reaffirmed
his faith in locality: "On one supposition we should, in my opinion, abso-
lutely hold fast: the real factual situation of the system (G) is independent
of what is done with the system (B) which is spatially separated from the
former." Einstein did not live to see Bell's proof and would certainly have
been surprised by Bell's refutation of his cherished postulate. But I think
he would have welcomed the strange news Bell's theorem brings us con-
cerning the true nature of the quantum world. Bell's result vindicates
Einstein's intuition that something funny is going on in quantum-corre-
lated two-particle states.

As in the case of the EPR paradox, it's important to realize what Bell
did not do. He did not discover an experimental situation in which non-

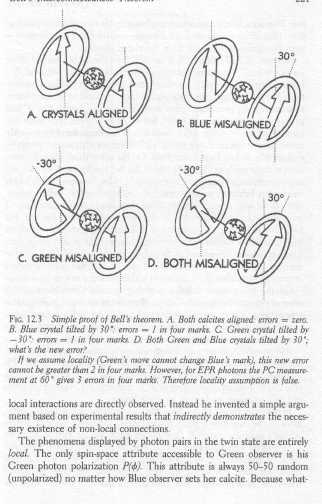
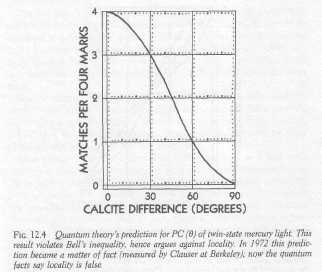
tinctive feature) but regarded by physicists as a kind of mathematical
fiction with no roots in reality. Since Bell's theorem demands a superlumi-
nal connection and quantum theory provides one—in the form of ubiqui-
tous but presumably "fictitious" phase connections—perhaps these quan-
tum connections are not as fictitious as was once believed.

Since there is nothing that is not ultimately a quantum system, if the
quantum phase connection is "real," then it links all systems that have
once interacted at some time in the past—not just twin-state photons—
into a single waveform whose remotest parts are joined in a manner un-
mediated, unmitigated, and immediate. The mechanism for this instant
connectedness is not some invisible field that stretches from one part to
the next, but the fact that a bit of each part's "being" is lodged in the
other. Each quon leaves some of its "phase" in the other's care, and this
phase exchange connects them forever after. What phase entanglement
really is we may never know, but Bell's theorem tells us that it is no limp
mathematical fiction but a reality to be reckoned with.

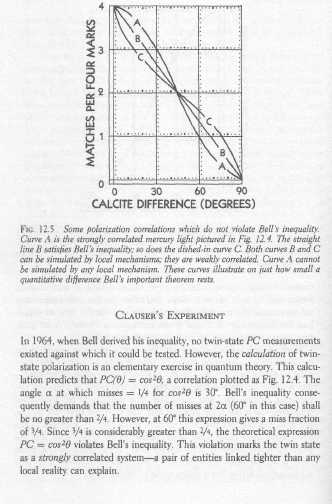
The fact that this calculated result violates Bell's inequality implies that
any system which obeys these quantum-theoretical predictions cannot be
explained by a local reality. Before Bell's discovery, one could still imagine
that a local reality lurked beneath the experimental facts; after 1964, one
could blissfully believe in a strictly local world only by hoping that quan-
tum theory was wrong in its predictions concerning photons in the twin
state.

Since it challenges one of physicists' most cherished beliefs—that the
world is fundamentally local—one might have expected Bell's proof to
explode like a bombshell in the corridors of science. Instead, Bell's proof,
published in an obscure little journal, was largely ignored even by those
physicists who managed to find out about it.

Most physicists are not impressed by Bell's proof because it deals with
reality, not phenomena. The majority of physicists are phenomenalists—
whose professional world is circumscribed by phenomena and mathemat-
ics. A phenomenalist perceives science as advancing in two directions: 1.
new experiments uncover novel phenomena; 2. new mathematics explain
or predict phenomena in original ways. Since it proposes no new experi-
ments and derives no new phenomena-relevant mathematics, but merely
puts certain constraints on an invisible reality, Bell's proof lies outside the
fashionable formula for success in science and is generally dismissed by
scientists as "mere philosophy."

Physicists' cool reception of Bell's proof is reminiscent of David Hume's
famous prescription for separating truth from nonsense: "Does it contain
any abstract reasoning concerning quantity or number? No. Does it con-
tain any experimental reasoning concerning matter of fact and existence?
No. Commit it then to the flames: for it can contain nothing but sophistry
and illusion."

In the midst of this climate of indifference toward theories of reality,
John Clauser, a young Ph.D. from Columbia, proposed actually to mea-
sure twin-state photons to see whether their polarization correlation attri-
bute satisfied Bell's inequality (world is local; quantum theory wrong) or
not (world is non-local; quantum theory right). Clauser received no sup-
port at Columbia for his proposal to put Bell's inequality to experimental
test, and moved to Berkeley where apparatus already existed which he
knew he could modify to measure twin-state photons.

Many kinds of excited atoms emit pairs of twin-state photons as they
return to their ground state. Most experiments carried out to test Bell's
inequality have used either mercury atoms excited by electron impact or

calcium atoms excited by laser light. Clauser's Berkeley mercury source
operates like a mercury-vapor streetlamp—both emit Blue and Green
twin-state light—but Clauser's source was smaller and more intense than
the lamps which nightly flood Telegraph Avenue with photons in the twin
state.

Because real photon detectors are not 100 percent efficient—they count
only about 10 percent of the photons which strike their phosphor
faceplates—one cannot simply compare Bell's inequality to experimental
results. Adapting Bell's original reasoning to existing experimental reali-
ties, Clauser and his colleagues derived a version of Bell's inequality (called
the "CHSH inequality" after John F. Clauser, Michael A. Horne, Abner
Shimony, and Richard A. Holt) which is testable with low-efficiency de-
tectors.

Clauser was motivated to test the Bell inequality by his strong faith that
the world was ultimately local. If quantum theory predicts a result which
conflicts (via Bell's proof) with locality, so much the worse for quantum
theory. Clauser anticipated that his experiment would prove quantum
theory wrong at least in this matter of twin-state polarization. The results
proved otherwise. In 1972 Clauser announced that quantum theory had
passed his test. Bell's inequality had been experimentally violated by Blue
and Green photons at Berkeley. Now not merely quantum theory but
quantum fact contradict the hypothesis that the world is linked up by
strictly local lines.

Aspect's Experiment

Clauser's pioneer test of the Bell inequality contains a loophole through
which a desperate logician might still derive a local world. To pinpoint this
loophole, let's return to our imaginary EPR experiment in space.

Clauser's mercury source sent Blue and Green light to opposite corners
of a room. Our spaceship lighthouse shoots photons to Betelgeuse and
Earth five hundred light-years apart.

Clauser switched the orientation of his P meters every 100 seconds.
Clauser's switching time, translated to cosmic lighthouse scale, corre-
sponds to keeping the P meters on Earth and Betelgeuse fixed for more
than a billion years. Such leisurely P measurements would permit informa-
tion on how distant P meters were set to leak between Earth and Betel-
geuse at sublight speed (carried perhaps in the gossip of interstellar tour-

ists)—information which could allow most of the photons to simulate
strong correlations by strictly local means. To block the possibility of sub-
luminal security leaks during long P-meter rests, the experimenter must be
able to change the P meters while the photons are in flight. To change a
calcite this fast in the lab means switching its orientation in a few bil-
lionths of a second.

Unfortunately, mere matter just can't move that fast. However, physi-
cist Alain Aspect at the University of Paris devised an experiment to test
Bell's inequality which uses two acousto-optical switches to deflect each
photon beam to one or the other of two preset calcite detectors. Instead of
rapidly moving his calcites, Aspect moves his light beams.

With his ultrafast switches, Aspect can measure a different polarization
every 10 billionth of a second, fast enough to eliminate subluminal secu-
rity leaks between Blue and Green P meters. If Aspect's twin-state pho-
tons violate Bell's inequality, the reality that underlies their strong correla-
tion must connect Green and Blue measurement stations at a speed
exceeding the velocity of light. Aspect completed his experiment in 1982,
verifying the strongly correlated quantum theoretical predictions, hence
violating Bell's inequality and supporting his contention that our phenom-
enally local world is in actuality supported by an invisible reality which is
unmediated, unmitigated, and faster than light.

Although Bell's theorem arose in the context of quantum theory, Bell's
result does not depend on the truth of quantum theory. The Clauser-
Aspect experiments show that Bell's inequality is violated by the facts.
This means that even if quantum theory should someday fail, its successor
theory must likewise violate Bell's inequality when it comes to explaining
the twin state. Physics theories are not eternal. When quantum theory
joins the ranks of phlogiston, caloric, and the luminiferous ether in the
physics junkyard, Bell's theorem will still be valid. Because it's based on
facts, Bell's theorem is here to stay.

Impossible Worlds

Bell's theorem is an important tool for reality research because it enables
folks who create imaginary worlds confidently to reject millions of impossi-
ble worlds at a single glance. Bell's theorem tells you right away: "If it's
local, it's hokum."
One of the worlds soundly obliterated by Bell's proof is the "distur-

bance model" of quantum reality. In this model—a species of neorealism
—quantum entities actually possess attributes of their own whether mea-
sured or not, but the measuring device changes these attributes in an
unpredictable and uncontrollable way. The inevitable disturbance of the
quantum system by the device which measures it gives rise, in this model
of reality, to quantum randomness, to the uncertainty principle and all the
other quantum oddities.

As a picture of how the quantum world might actually operate, many
physicists who have not given much thought to the matter take refuge in
some vague disturbance model of reality. For several years I avoided think-
ing about the quantum reality question by supposing that a disturbance
model of some kind was sufficient to account for the strange quantum
facts.

Such a disturbance model would explain, for instance, the observed
polarization of the Green photon in the EPR experiment as a result of the
Green calcite's "uncontrollable disturbance" of some intrinsic Green pho-
ton attribute. In other words, this model explains Green observer's results
by appealing to a hypothetical mechanism which involves only the Green
photon and the Green calcite. Bell's theorem shows that any such local
mechanism, no matter how ingenious, simply fails to fit the quantum
facts: Bell's proof knocks out the disturbance model because it's local.

Facile popular expositions often invoke the disturbance model of mea-
surement to justify Heisenberg's uncertainty principle: we cannot know a
quantum entity as it is because we must inevitably disturb whatever we
observe. Bell's result shows this notion of quantum measurement as local
disturbance to be as outdated as the obsolete picture of the atom as
miniature solar system.

Another type of impossible world is the "classical style" reality symbol-
ized by Newton's apple. Apples, and everything else in such a world, are
truly ordinary objects which possess attributes all their own even when not
being measured. When measured, whether by man, woman, or machine, a
classical apple merely reveals some attributes which it previously pos-
sessed.

Such an apple world (which experts call a "local non-contextual real-
ity") is not inconceivable or illogical. But, according to Bell's theorem,
apple world is impossible because it can't possibly fit the facts. As a model
for the world we actually live in, apple world and all its local non-contex-
tual cousins are, by virtue of their locality, sheer fantasy worlds.

We obviously need to be more sophisticated in our choice of possible

worlds. Let's imagine, for instance, a relational reality patterned after the
notions of Niels Bohr. The entities that make up such a world are like
rainbows: they do not possess definite attributes except under definite
measurement conditions. Upon measurement, attributes do emerge but
they are a joint possession of entity and M device. In such a rainbow
reality (called "local contextual"), attributes are not innate to an entity
but change when the conditions of observation change. The only restric-
tion we place upon such observer-induced changes is that distant M de-
vices cannot change an entity's condition if such an influence would re-
quire a faster-than-light signal. In such a contextual, but local, reality, only
nearby observers take part in the determination of an entity's apparent
attributes.

Like apple world, rainbow world is neither inconceivable nor illogical. It
is simply, on account of its locality, not the sort of world we happen to live
in.

Bell's theorem rejects apple worlds; it also rejects rainbow worlds. What
kinds of worlds does Bell's theorem allow?

A Possible World

Imagine Joe Green, an inhabitant of a non-local contextual world. Up in
his sky, Joe sees a rainbow made up of a glistening pattern of colored dots.
Unlike the regular dots in a photographic halftone, Joe's rainbow's dots
form a random array.

On the other side of the same sun lies a counter-Earth, where Suzie
Blue watches another rainbow in her counter-sky. Suzie's rainbow is like-
wise composed of a random array of colored dots. When Joe Green moves
his chair, his rainbow moves too (a rainbow's position attribute is contex-
tual, not innate), but Suzie's rainbow stands still. However, when Joe
moves his chair Suzie's random array 200 million miles away instantly
changes into a different (but equally random) array of colored dots. Suzie
is not aware of this change—one random array looks pretty much like any
other—but this change actually happens whether she notices it or not.

The phenomenon in this hypothetical world, whether the rainbow
moves or not, is completely local: Suzie's rainbow doesn't move when Joe
changes places. However, this world's reality—the array of little dots that
make up both rainbows—is non-local: Suzie's dots change instantly when-
ever Joe moves his chair.

Such a non-local contextual world, in which stable rainbows are woven
upon a faster-than-light fabric, is an example of the kind of world permit-
ted by Bell's theorem. A universe that displays local phenomena built
upon a non-local reality is the only sort of world consistent with known
facts and Bell's proof. Superluminal rainbow world could be the kind of
world we live in.

During the past twenty years Bell's theorem has been proved in many
ways, some of which refer to photon attributes and some which don't. My
version of Bell's proof makes no essential use of the concept of a photon or
its attributes. Although Green and Blue photons and their polarization
attributes are mentioned to familiarize you with the details of the EPR
experiment, when it comes to the proof of Bell's theorem my argument is
formulated entirely in terms of a pair of binary messages printed by partic-
ular macroscopic objects. I prove Bell's theorem here in terms of moves
(orientations of calcite crystals) and marks (ups and downs on a data tape).

Bell's theorem as a relation between moves and marks takes non-locality
out of the inaccessible microworld and situates it squarely in the familiar
world of cats and bathtubs. Expressed in thoroughly macroscopic lan-
guage, Bell's theorem says: In reality, Green's move must change Blue's
mark non-locally. From arguments based on phenomena alone (no appeal
to hidden attributes) we conclude that clicks in a certain counter must be
instantly connected to the movement of a distant crystal of calcite.

For anyone interested in reality, Bell's theorem is a remarkable intellec-
tual achievement. Starting with fact plus a bit of arithmetic, Bell goes
beyond the facts to describe the contours of reality itself. Although no one
has ever seen or suspected a single non-local phenomenon, Bell proves
conclusively that the world behind phenomena must be non-local.

If all the world's phenomena are strictly local, what need is there to
support local phenomena with a non-local fabric? Here we confront an
alien design sense bizarre by human standards: the world seems strangely
overbuilt. In addition the world's superluminal underpinning is almost
completely concealed—non-locality would have been discovered long ago
if it were more evident; it leaves its mark only indirectly through the
impossibly strong correlations of certain obscure quantum systems.

In his celebrated theorem, Bell does not merely suggest or hint that
reality is non-local, he actually proves it, invoking the clarity and power of
mathematical reasoning. This compulsory feature of Bell's proof particu-
larly irks physicists whose taste in realities is strictly local.

Bell's important proof has caused a furor in reality research comparable

to the Einstein-Podolsky-Rosen scandal of 1935. On the one hand, Bell's
theorem proves the existence of an invisible non-local reality. Those who
prefer their realities to be local have so far not been able to refute Bell's
argument. The fact that Bell's proof is remarkably clear and brief has not
hastened its refutation.

On the other hand, although Bell's theorem indirectly necessitates a
deep non-locality, no one has come up with a way to directly display this
purported non-locality, such as a faster-than-light communication scheme
based on these deep quantum connections. If reality research's bottom
line is "Reality has consequences," then this Bell-mandated deep reality
has so far failed to make a showing. What the future holds for Bell's
instantly connected but as yet inaccessible deep reality is anyone's guess.

13 -

The Future
of Quantum Reality

"Strikes at the source of daily confusion
Eliminates ignorant fantasy
Scrubbing your senses free of Illusion
Enjoy the taste of Reality;
Scrubbing your senses free of Illusion
Enjoy the taste of Reality."

---"Reality Calypso" from
Benjamin Bunny Faces Reality

Bell's proof has the logical form reductio ad absurdum, namely:

1.  Make an assumption A;

2.  Show that it leads to a contradiction; hence

3.  Conclude that assumption A is false.

To prove his theorem, Bell assumes a local reality, shows (with a bit of
arithmetic) that this contradicts experimental fact, then concludes that no
local reality can underlie these facts. Hence reality is non-local.

Reductio ad absurdum proofs are particularly vulnerable to refutation
because it's impossible to make just one assumption. Along with major
assumption A, lots of little minor assumptions a, b, c, d, inevitably creep
in. If you're particularly fond of assumption A, you can derail the proof of
its absurdity by blaming the logical contradiction on assumption b instead.

In the case of Bell's proof, one can continue to believe in a local reality
by denying one of Bell's other assumptions instead. However, because
Bell's proof is so short and most of his assumptions accessible to experi-
ment, such additional suppositions are not easy to find. Hence the various
negations of Bell's conclusion tend to be rather farfetched and lead to
realities more preposterous than the superluminal reality they attempt to
exorcise.

Attempts to Refute Bell's Proof

Consider, for example, Cornell physicist N. D. Mermin's curious argu-
ment that since Bell assumes a local reality, we can blame the contradic-
tion either on the locality assumption or on the assumption of "reality."
Mermin wants to keep locality, so as far as he is concerned, reality must
go. Mermin uses Bell's reductio ad absurdum method to conclude that
"the moon is demonstrably not there when nobody looks."

It's difficult to convey to outsiders the distaste which the majority of
physicists feel when they hear the word "non-locality." Physics, after all, is
full of odd notions. What's so repulsive about a mere faster-than-light
connection? Mermin's argument illustrates, more than words can say, the
deep antipathy most physicists bear toward unmediated action-at-a-dis-
tance: these guys so treasure locality that they are willing to deny reality
itself before accepting a world that's non-local.

However, when you hear a physicist saying that he "denies reality," take
it with a grain of salt. Don't imagine the poor guy believes that every-
thing's a dream. He just means to say that the reality he's got in mind is a
bit unconventional. Physicists who deny reality altogether cease to be
physicists and their insights do not appear in physics journals.

The form of Mermin's conclusion shows that he believes in a reality of
the observer-created variety—what I've called "rainbow reality" because
of the observer-dependence of the rainbow's position attribute. Rainbow
reality can come in two flavors: local rainbow reality (Green observer cre-
ates only Green code) or non-local rainbow reality (Green observer helps

create Blue code too). It's easy to show (via Bell's argument) that a local
observer-created reality contradicts the quantum facts just as surely as does
Bell's original local (but otherwise unspecified) reality.

Mermin's desperate attempt to escape the demon of non-locality by
accepting a reality that's observer-created simply doesn't work. The mild
kind of observer-created realism sanctioned by quantum theory—namely,
that dynamic attributes are relational—has to be non-local to fit the facts.
Opt for a rainbow reality if you will, but it's got to be superluminal.

Many scientists read the weekly journal Science to learn what's happen-
ing outside their fields. Reporting on the Aspect experiment, Science staff
writer Arthur Robinson speaks for many physicists when he observes that
Bell's assumption A is actually two assumptions: locality plus realism. "Re-
alism," according to Robinson, "requires that the [polarization attributes]
exist and have definite values whether or not they are measured." Instead
of giving up locality, suggests Robinson, why not simply abandon realism?
However, those who have followed me so far will see that Robinson's
realism corresponds to what I call "apple world": a universe in which
entities possess their attributes in the familiar classical manner indepen-
dent of observation. Even the color of beefsteak is not "real" according to
Robinson's standards.

Banishing Bell-guaranteed non-locality by giving up apple world would
be a cheap victory indeed. If it would restore locality, most physicists
would gladly relinquish classical-style reality, especially when they recall
that in 1932 John von Neumann had already proved that kind of reality to
be incompatible with quantum theory. Unfortunately you can give up a
lot more than apple reality and still be stuck with non-locality.

For instance you can deny the existence of photons and all their attri-
butes, both static and dynamic (no physicist goes this far)—but the world
that's left (mostly macroscopic measuring devices and their responses) still
needs to be superluminally linked. Look at the version of Bell's theorem
presented in the previous chapter: it assumes nothing concerning the hy-
pothetical attributes of photons, but deals solely with the measurement
results (marks) of measuring devices in specified configurations (moves).
Provided that when you deny reality you retain a belief in the real exis-
tence of measuring devices, their settings, and their results, Bell's proof
shows that the operations of such machines must be non-locally con-
nected. Bell's quantum connection not only conjoins the attributes of
invisible microentities, but links as well the actions of heavy apparatus
made of steel, glass, and calcite. In the EPR experiment, Bell's deep non-

locality leaks into the macroscopic world, manifesting as superstrong rela-
tions between distant detection devices.

In my opinion, you can escape Bell's conclusion (reality is non-local) by
denying reality only if you go all the way and claim that macroscopic
objects (including measuring devices) are somehow not really there.
Bishop Berkeley did not believe in the existence of mountains, apples, or
polarization meters, but few physicists—even those committed to locality
at all costs—are willing to go so far. Denying the evidence of your senses
seems a high price to pay just to win an argument. Perhaps the world
really is non-local.

There are, however, more subtle objections to Bell's proof. To visualize
what's called the "CFD assumption," let's return to the EPR experiment
in the form of a spaceship lighthouse beaming Green photons to Earth
and Blue to Betelgeuse. Consider the locality assumption in the form:
Green's move does not change Blue's mark.

This form of the locality assumption means that whether Green sets his
calcite at twelve o'clock or two has no effect on Blue's result. But for each
particular photon pair, Green can set his calcite at only one angle. Because
of this experimental fact of life, the locality assumption actually breaks up
into two parts: 1. if Green had set his calcite at some angle other than the
one he actually chose, definite (but unknown) results would have occurred
for both Green and Blue; 2. Blue's result for this hypothetical setting
would have been the same as Blue's result for Green's actual setting.

Part one of the locality assumption supposes that if Green had chosen
to carry out some other P measurement, Blue would have obtained some
result. This assumption (known to quantum reality aficionados as con-
trafactual definiteness, or CFD, for short) is untestable because for each
photon pair, Green can make only one kind of P measurement. Einstein,
Podolsky, and Rosen also had to assume CFD in their celebrated proof for
the existence of extra "elements of reality" not described by quantum
theory. In my pizza pie analogy, the CFD assumption means that I take
for granted the notion that ordering any kind of pizza other than the one I
did in fact order would have resulted in its delivery. This CFD assump-
tion, that hypothetical actions would have led to definite outcomes, seems
reasonable but it is by its very nature untestable since each event happens
only once. You can order only one pizza this Saturday night; Green can
only align his P meter in one direction for photon #1136.

Part two of the locality assumption brings in the notion of locality per
se: it asserts that Green's hypothetical acts do not affect Blue's hypotheti-

cal results. Because locality is expressed in terms of hypothetical results—
the results of choices we could have made but did not—we see that unless
we assume CFD, we cannot even formulate the notion of locality in Bell's
sense. Die-hard fans of a local universe seize on this logical loophole and
attempt to refute Bell's conclusion by denying CFD.

One of the most prominent physicists trying to rescue locality by dump-
ing CFD is John Wheeler. Wheeler denies CFD this way: "[Bell's theo-
rem] deals with worlds that never were and never can be. The real world is
what we care about here." Wheeler attempts to invalidate Bell's theorem
not by denying reality, but by upholding it in a very strict sense.

Contrafactual reasoning is the basis for personal, business, and military
planning. The outcome of chess games and more serious conflicts is con-
trolled not so much by actual events as by hypothetical threats and pos-
sibilities that never happen, but which could have happened had you
acted otherwise. Reasoning in terms of hypothetical outcomes takes con-
crete form in contingency plans for nuclear attack and in computer chess
decision trees which simply take the CFD assumption for granted. Why
CFD is justified in the case of the hypothetical outcomes of conceivable
(but perhaps "unthinkable") nuclear options, but not in the case of
equally macroscopic P meter outcomes is hard for me to understand.

Contrafactual reasoning is so deeply rooted in human thinking that it's
difficult even for determined opponents of CFD to eliminate it from their
arguments. For instance, in order for John Wheeler's celebrated delayed-
choice experiment (discussed in Chapter 9) to make sense, he must com-
pare the outcome of experiment A not with the outcome of experiment B
but with the outcome that would have occurred had experiment B been
performed instead of A, a manifest example of CFD-infected reasoning.

Another way of gauging the plausibility of the no-CFD objection to
Bell's theorem is to ask, "In what sorts of conceivable worlds would CFD
be a patently invalid assumption?" One such no-CFD world is a universe
where only one history was ever possible in the first place. To speak of
hypothetical results in such a one-track world would be to talk nonsense.
This kind of no-CFD world is strictly deterministic in the Newtonian
clockwork style. Because of the absence of real choices, Bell's theorem can
not even be formulated in a strictly Newtonian universe.

One way to evade Bell's theorem's non-local consequences would be to
devise a local model of the quantum world in which CFD is a patently
invalid assumption. No one, to my knowledge, has been clever enough to

come up with such a local no-CFD picture of the world compatible with
quantum theory.

Other attempts to invalidate Bell's theorem involve challenging West-
ern (i.e., Boolean) logic, denying Green observer's free will or practicing
subtle variations on the no-CFD theme. The arguments against Bell's
theorem (and their counterarguments) have become so recondite that a
meeting of physicists on this topic sounds much like a congress of medi-
eval theologians.

Physicists continue to debate whether Bell's theorem is airtight or not.
However, the real question is not whether Bell can prove beyond doubt
that reality is non-local, but whether the world is in fact non-local.

Do Non-local Connections Permit Superluminal

Signaling?

Whether deep reality is truly non-local or not could be settled in an
instant by the discovery of a single superluminal signal. If the world is in
truth bound together everywhere by faster-than-light connections, can we
exploit these links to send superfast messages to our friends? Such an
accomplishment would not only directly validate Bell's conclusion, it
would initiate a new era for humankind, making us masters of space and
time.

If we could exploit the quantum connection, Superman flying faster
than light, hence going backward in time to save Lois Lane, need not
happen only in the movies. According to Einstein's relativity, superlumi-
nal signals would open up similar channels from the present to the past—
channels that would allow people today to change what by conventional
reckoning has already happened. The fact that FTL signaling entails back-
ward causality is regarded by some physicists as a powerful argument
against the possibility of such signaling (and against non-locality in gen-
eral) but the achievement of an actual FTL transmitter would obviously
invalidate such philosophical objections.

In the EPR photon lighthouse, the natural quantum process that blocks
FTL signaling is quantum randomness. Put yourself on Betelgeuse with
Blue observer. No matter how she sets her Blue crystal, she receives a
message from the central spaceship which consists of a 50-50 random
pattern of ups and downs. When Green observer on Earth moves his
calcite we know (via Bell's theorem) that his actions must change Blue's

sequence of marks. Some or her ups change to downs and vice versa; it this
did not happen, the correlation would be weaker than is in fact observed.
However, these changes in the details of Blue's marks involve a shift from
one random pattern to another equally random pattern. Since all random
sequences look alike (although there are many kinds of order, there is only
one kind of randomness), Blue is not aware of this Green-initiated change.
The situation seems to be that Green can send superluminal messages but
Blue cannot decode them.

Even if we believe (with the support of Bell's theorem) in universal
superluminal links, we must face the possibility that such links are private
lines accessible to the workings of nature alone, and are blocked to human
use by an undecipherable scrambler built of perfect quantum randomness.

Eberhard's Proof Contra Superluminal Signaling

To the welter of proofs discussed so far—von Neumann's proof (against an
ordinary-reality explanation of quantum theory), EPR's proof (for extra
"elements of reality" ignored by quantum theory), and Bell's proof
(against a local deep reality)—I am compelled to add one more. If quan-
tum theory is correct, then it is possible to prove that quantum measure-
ments cannot be used to send signals faster than light.

This result, first obtained by Berkeley physicist Philippe Eberhard, gen-
eralizes Green's failure to send a recognizable signal to Blue via strongly
correlated twin-state photons. Eberhard's proof states that even in the
midst of a superluminal reality, no quantum measurement results can be
connected faster than light.

Eberhard's proof, unlike Bell's, depends on the validity of quantum
theory. Eberhard uses quantum theory to calculate the effect of one
"quantum measurement" (such as Green's choice of move) on another
"quantum measurement" (such as Blue's pattern of marks) carried out on
a phase-entangled system such as a pair of photons in the twin state.
Eberhard's calculation shows that whatever the behavior of individual
marks may be (because it's strictly statistical, quantum theory does not
concern itself with individual events), the pattern of marks does not de-
pend at all on these faraway moves. Individual message bits may conceiv-
ably change faster than light; since these bits occur at random we can
neither verify nor disprove this claim. But according to Eberhard, the

pattern of such bits remains precisely the same no matter how the distant
detector is manipulated.

A "quantum measurement" is defined as a statistically discernible differ-
ence. Since there is no statistical difference between random sequences,
the two random Blue sequences that may result when Green makes two
different moves do not count as two quantum measurements. Thus
Eberhard's proof permits nature to send perfectly encrypted messages
along FTL channels but denies humans access to such channels so long as
their actions are bound by the rules of quantum theory.

Several ingenious schemes have been devised to evade Eberhard's proof,
based primarily on attempting to exploit the ambiguity that exists over
what actually constitutes a quantum measurement, but all such schemes
have so far failed. Skeptical scientists compare the attempt to construct
real superluminal communicators based on strong quantum correlations in
the face of Eberhard's impossibility proof with attempts which flourished
in the last century to devise perpetual motion machines in the face of the
law of energy conservation.

Barring an unforeseen breakthrough in superluminal communication
research, the small part of the physics community concerned with reality
research now splits into two parts: those who can prove non-local influ-
ences but cannot exploit them, and those who don't believe in Bell-guar-
anteed FTL links but can't refute them. How this tension at the heart of
physics will ultimately be resolved lies in the unknown future. Meanwhile
let's look at how Bell's discovery has affected physicists' reality crisis. How
does Bell's theorem change our perception of the eight quantum realities?

Bell's Theorem and Reality

Basically Bell changed our view of reality by raising the issue of non-
locality. After Bell, any serious model of reality has to be either manifestly
non-local or custom-designed to render the locality/non-locality distinc-
tion meaningless. In any case, in this post-Bell era every quantum realist
must deal with non-locality in one way or another.

Quantum Reality #1: The Copenhagen interpretation, Part I (There
is no deep reality). Bohr believed that quantum entities possess no dy-
namic attributes of their own: such attributes as we measure them to
possess are a joint product of quon and M device. According to the Co-

penhagen interpretation a quon's so-called attributes (excluding its static
attributes) belong not to the quon itself but to "the entire measurement
situation."

Bell's theorem tells us that Bohr's insight that dynamic attributes are
creatures of the measurement situation is essentially correct: the notion
that a quon's attributes are innate must be abandoned because of its
blatant locality. However, "the entire measurement situation" which de-
termines a quon's attributes is more extensive than Bohr could have fore-
seen. Like everyone else in his day, Bohr was a firm believer in locality.
However Bell's theorem demonstrates that "the entire measurement situa-
tion" which decides what values Blue's attributes will display must include
the setting of Green's crystal located possibly half a galaxy away. Bohr
built better than he knew: what happens in his "rainbow reality"—a world
of relational attributes—must depend not only on observers nearby but
superluminally on "the entire experimental arrangement" no matter how
distant.

Quantum Reality #2: The world is created in the act of observation.
The notion that quons acquire their dynamic attributes via the act of
observation is a cornerstone of the Copenhagen interpretation. Bell's theo-
rem merely expands the notion of observer to include the action of people
and apparatus at arbitrarily distant locations—locations outside the reach
of conventional light-speed-limited signals.

It's important to understand that Bell's theorem requires reality, not
phenomena, to be superluminally linked. Measurement is the means by
which a physicist makes contact with reality. All quantum measurements
are made up of quantum jumps—the individual ups and downs of a partic-
ular M device, or the flashes on a phosphor screen, for example. Quantum
phenomena consist of the persistent and repeatable patterns which these
leaping quanta form. These patterns are bound to be local, by Eberhard's
proof, and have never been observed to be otherwise. On the other hand
the quanta themselves—the unpredictable alphabet which spells out the
words and paragraphs of the world's phenomena—must be non-locally
connected, according to the theorem of John Bell.

Quantum Reality #3: The world is an undivided wholeness. The no-
tion that the world is an inseparable whole arises from the presence in
quantum theory of "phase entanglement." In the quantum formalism,
two quons that have once interacted do not separate into two waveforms

when they move apart but are forever afterward represented as a single
wave. Whether this wholeness of representation is matched by a wholeness
of being is a question that was posed by certain thoughtful physicists,
especially Erwin Schrodinger and David Bohm.

Although superluminal phase entanglement is necessary to make the
answers come out right, it never leads to any superluminal results. Since
these instant connections which bind separated quons into a seamless
whole (in the formalism, at least) never surface in the world of phenom-
ena, most physicists regarded them as purely formal features of the quan-
tum language—necessary for calculation but having no counterpart in
reality.

Bell's theorem shows that the holistic grammar of the quantum formal-
ism reflects the inseparable nature of reality itself. Beneath phenomena,
the world is a seamless whole.

Although it points beyond phenomena, Bell's theorem is proved by
arguments drawn solely from the facts. Because of its strictly phenomenal
base, Bell's theorem by itself gives no hint as to the mechanism by which
reality might achieve its necessarily non-local connections. These ubiqui-
tous phase connections in the quantum formalism offer a non-classical
image for how a non-local world might work: quons are instantly con-
nected not because something stretches between them but because each
has left part of itself in the other, a part to which it retains immediate
access.

Quantum Reality #4: The many-worlds interpretation. Bell's theorem
has nothing to say directly about the many-worlds interpretation because
in Everett's luxurious universes you cannot prove Bell's theorem.

The subtle but necessary CFD (contrafactual definiteness) assumption
takes for granted that for each photon pair in the EPR experiment a
particular hypothetical calcite setting will lead to a definite result. In the
many-worlds model of reality, each measurement setting leads to all possi-
ble results. The Everett multiverse violates the CFD assumption because
although such a world has plenty of contrafactuality, it is short on definite-
ness.

Although Bell's theorem does not apply to an Everett-style universe,
there's plenty of non-locality present without it. Any model of reality in
which a tiny event in the Andromeda galaxy can instantly split my reality
into thousands of Xerox copies cannot by any stretch of the imagination
be called "local."

Quantum Reality #5: Quantum logic (The world is put together like a
non-Boolean lattice). To cover the facts takes more than logic. Quantum
logic, like its Boolean cousin, codifies just the bare bones of talk about
quantum attributes. It provides not a complete quantitative picture of
quantum phenomena, but a mere logical skeleton which needs to be
fleshed out by more specific quantitative relations.

Bell's proof cannot be derived from qualitative arguments but depends
for its validation on specific numerical relationships. See Fig. 12.5 for an
illustration of just how small an experimental difference separates a non-
local reality from its local competition. Quantum logical relations merely
outline the phenomena and do not provide specific quantitative informa-
tion. Bell's theorem can't be proved from logic lattices alone.

It has been suggested that even though one cannot prove Bell's theorem
via quantum logic, perhaps one can disprove it. To prove this theorem, you
must have recourse to ordinary Boolean logic; if the world's logic is other-
wise, perhaps this proof doesn't go through. However, even quantum logi-
cians use Boolean logic when it comes to talking about quantum logic. In
other words, the metalogic of quantum logic is Boolean.

In addition, quantum logic is the consequence of a particular assump-
tion about a quon's attributes. If you assume that photons have attributes
of their own, then these attributes must follow a non-Boolean arithmetic.
On the other hand, if you assume that a photon's attributes are relational,
ordinary logic suffices. Since the version of Bell's theorem presented here
makes no assumptions at all about photon attributes, the concept of quan-
tum logic is irrelevant.

Bell's theorem likewise has not provided new insight into the meaning
of non-Boolean relations. Of all quantum realities, Bell's logical necessity
of non-local connections seems to illuminate quantum logic the least.

Quantum Reality #6: Neorealism (The world is made of ordinary
objects). Von Neumann's proof outlaws objects with innate attributes.
Bell's theorem also forbids such ordinary objects and in addition rejects all
entities whose relational attributes depend only on the settings of local M
devices. If these proofs are valid, the only kinds of entities which can make
up the quantum world are those whose attributes depend non-locally on
the settings of distant measuring devices.

Most neorealist models consider the world to be built in the old-fash-
ioned classical manner, out of particles and fields. Models of quantum

reality constructed according to this plan possess the peculiar feature that
the fields which connect each particle to its environment seem to be
capable of instantly switching a particle's attributes in response to a con-
figuration change anywhere in the universe.

Such particle/field models of the world are not unmediated, because
changes in a particle's attributes are carried by a field rather than mysteri-
ously jumping from one point to another. However, this field—called the
pilot wave—must be able to transmit information faster than light with-
out attenuation. Thus although these neorealist worlds are mediated (by
pilot waves), they are still unmitigated and immediate.

For a physicist the most unpleasant feature of these neorealist models is
the presence of real fields that move faster than light. Bell's theorem
shows that the appearance in neorealist schemes of fields capable of super-
luminal data transmission is no accident: any model of reality which fits
the quantum facts must possess some means of exchanging information
faster than light.

Determined foes of superluminal connections cannot agree which op-
tion is more repulsive: the real superluminal fields of the neorealists, which
explicitly carry signals from place to place at FTL velocities, or the voo-
doo-like unmediated influences suggested by the quantum formalism,
which simply jump directly from Earth to Betelgeuse.

Quantum Reality #7: Consciousness creates reality. Bell's theorem
says that if consciousness does indeed create reality, it cannot be a purely
local matter. The decision of a mind here must be able to change the value
of an attribute there, where here and there may be separated by immense
distances.

Rash speculations that this strong quantum connection permits telepa-
thy or long-distance mind-over-matter effects need to be balanced by the
realization that Bell's theorem concerns only reality—that is, raw quan-
tum jumps—not phenomena, the regular patterns of quantum jumps.
Thus even if consciousness could create reality, the power of mind to
intervene in distant happenings may be limited to the production of sin-
gle, statistically unusual events—the so-called outriders or glitches that
show up from time to time in even the most well-controlled experiment.

That faraway minds can alter the fabric of reality but not the pattern
woven thereon need not limit minds to the production of trivial deeds.
Some physicists believe that the whole physical universe originated out of
nothing as a single quantum jump—just the sort of wild, unpredictably

unique quantum event that a mind could initiate without upsetting the
statistical applecart.

Quantum Reality #8: The duplex universe. Werner Heisenberg was
one of the few quantum physicists who tried to imagine what unmeasured
quantum reality might look like. According to Heisenberg, the world sans
M devices is not fully real but consists of a superposition—a particularly
intimate quantum style of coexistence—of half-real "tendencies for be-
ing" which he called potentia. The advantages of such an attenuated style
of being is that many contradictory tendencies can coexist, an option not
open to solid facts; the price of non-contradiction is that none of these
tendencies is completely "real." Upon measurement, but not before, one
of these tendencies is selected, apparently at random, from the flock, and
promoted to full reality status. The essence of measurement, in Heisen-
berg's duplex world, is the sudden transformation of potentia into actual-
ity.

Bell's theorem requires that this measurement-induced transition from
soft possibility to hard actuality cannot be local but must depend on other
measurements going on at locations arbitrarily distant.

Heisenberg's model is an unusually explicit version of observer-created
reality. Unlike other proponents of observer-created reality, he tries to
imagine what reality is like before observation. Heisenberg declares the
raw material of the universe to be potentia, tendency, possibility—a world,
in a word, founded on a wave of opportunity. Bell's theorem applied to
Heisenberg's picture requires that these oscillating opportunities be linked
together faster than light.

This brief review of the eight quantum realities in the light of Bell's
proof shows that Bell's theorem does not resolve the quantum reality
question in favor of one reality or another. As long as they leave room for
non-locality, all eight of these realities are viable candidates for a model of
"the way the world really is."

What Bell's theorem does do for the quantum reality question is to
clearly specify one of deep reality's necessary features: whatever reality
may be, it must be non-local. Since Clauser's experimental verification of
Bell's theorem, we know that any correct model of reality has to incorpo-
rate explicit non-local connections. No local reality can explain the type of
world we live in.

Furthermore, since Bell's result is based on experimental facts, it is

independent of whether quantum theory is correct or not. Should quan-
tum theory someday fail in its predictions or simply be replaced by an
entirely different way of predicting the same quantum facts, Bell's theo-
rem would still be valid. Although it arose in the context of disputes about
the completeness of quantum theory, Bell's theorem is derived from the
facts themselves, not from any particular theoretical representation of
these facts.

Bell's theorem has illuminated one corner of deep reality, but the reality
crisis in physics is far from over; as yet no physicist can tell you what sort
of world we happen to live in. I speculate next on a few directions the
quest for quantum reality might take.

Can We Devise an Explicitly Holistic Model of
Measurement?

One of the most artificial features of quantum theory is its division of the
world into two parts: system and M device. The quantum formalism im-
plies that the world is a seamless whole, yet the first step in any quantum
computation is to fracture that unity.

In the all-quantum interpretation of measurement a von Neumann
chain stretches between system and observer, and the measurement prob-
lem consists of where to "break" that chain. In light of quantum whole-
ness, representing a measurement as a linear chain with definite beginning
and end seems like a bad way to start. Perhaps the von Neumann chain,
rather than being broken, should be welded together into a loop to form
what we might call a von Neumann ring.

In such a scheme (admittedly vague), the measuring device would pro-
vide a context for the quantum system's attributes while at the same time
its constituent quantum systems would provide a context for the attributes
of the M device. Each quantum entity would measure the other, closing
the circle and achieving a self-contained and consistent model of the
measurement process.

This vision of systems measuring one another would allow for the exis-
tence of autonomous realities without the need for human observers. In a
world consisting of communities of mutually scrutinizing measurement
loops, few quons would not belong to at least one such community. Even
those entities that have ceased to interact conventionally with their fel-

lows would be implicated in one or more von Neumann rings via non-local
phase entanglement.

This hypothetical reality made up of von Neumann rings takes Bohr's
view to the limit: it is thoroughly relational, containing no privileged
entities of any kind; a world entirely thingless, full of quons like rainbows
which are themselves made of rainbows.

Another possible direction for reality research would be the actual ex-
ploration of the multiple worlds suggested by Everett's interpretation of
quantum theory.

According to Kant, humans cannot experience reality itself because our
senses and brains were developed for more mundane purposes. For in-
stance, one of the biggest lessons that Einstein's special theory of relativity
teaches us is that, in reality, this world is four-dimensional. Although
humans experience a three-dimensional world in which time seems to
flow, reality itself exists in space-time—in which time is a dimension on a
par with space. Hermann Minkowski, one of Einstein's colleagues, intro-
duced the four-dimensional structure of the world this way to his students:

"The views of space and time which I wish to lay before you have
sprung from the soil of experimental physics, and therein lies their
strength. They are radical. Henceforth space by itself, and time by itself,
are doomed to fade away into mere shadows, and only a kind of union of
the two will preserve an independent reality."

If time is just another dimension, then the entire history of the universe
from beginning to end is spread along this time line. The past still exists
and so does the future. Our human perception of an eternal present which
seems to travel along in the future direction is an illusion: that's not the
way the world is at all. Physicist Hermann Weyl expressed the four-dimen-
sional view of things this way: "The objective world simply is; it does not
happen."

With what authority do physicists deny their immediate experiences to
claim that the world's really four-dimensional? Just this: if they don't write
the equations of physics in four dimensions (and instead write them in
three space dimensions plus a changing temporal dimension), they get
answers that agree with the experience of stationary observers but not
with observers moving relative to them. To accurately describe electrical
and mechanical phenomena in a manner valid for all observers, physicists
have to visualize the world in space-time, not in space plus time.

Likewise, in quantum theory physicists must describe the unmeasured

world as a simultaneous superposition of all its possibilities at once. If they
leave out a single possibility, they get the wrong answer. However, we do
not experience the world as a superposition of possibilities, but only as a
one-at-a-time sequence of definite actualities. Once again human percep-
tion of things seems out of step with reality.

No matter how sophisticated our concepts, we cannot help but perceive
the world, according to Kant, except through particularly human filters.
Even if we knew better, we couldn't tear off our colored spectacles and
look at the world as it really is. In this Kantian spirit Heisenberg describes
how phenomena inevitably appear classical to humans (Cinderella effect)
despite signals from physics that reality itself is anything but classical:

"Any experiment in physics, whether it refers to the phenomena of
daily life or to atomic events, is to be described in the terms of classical
physics. The concepts of classical physics form the language by which we
describe the arrangement of our experiments and state the results. We
cannot and should not replace these concepts by any others . . . The use
of classical concepts is finally a consequence of the general human way of
thinking . . . There is no use in discussing what could be done if we
were other beings than we are."

The source of all quantum paradoxes appears to lie in the fact that
human perceptions create a world of unique actualities—our experience is
inevitably "classical"—while quantum reality is simply not that way at all.
Quantum reality consists of simultaneous possibilities, a "polyhistoric"
kind of being absolutely incompatible with our merely one-track minds.

If these alternative universes are really real and we are barred from
experiencing them only by a biological accident, perhaps we can mechani-
cally extend our senses—as we have in so many other cases—with a sort of
quantum "microscope" which would allow us to actually experience some
of Everett's parallel universes firsthand. Since physics assures us that our
lives are embedded in a thoroughly quantum world, is it so obvious that
our experiences must remain forever classical?

Is Consciousness a Type of Quantum Knowledge?

Although it seems to be true that every physics experiment is classical in
form if not in content, is it so obvious that the full range of human
experience is also absolutely classical?

Science's biggest mystery is the nature of consciousness. It is not that
we possess bad or imperfect theories of human awareness; we simply have
no such theories at all. About all we know about consciousness is that it
has something to do with the head, rather than the foot. That's not much
but it appears to be more than the ancient Egyptians knew: the Egyptians
threw away the brain before beginning their elaborate embalming proce-
dures, judging it to be a mere accessory.

Is it possible that consciousness is some sort of quantum effect? Is
human awareness a privileged access to the "inside" of the quantum
world, an open door to some brain quon's realm of possibility? Can we
know firsthand what it is like to dwell in the quantum world just by sitting
still and looking inside our heads?

Human mental experience seems to be of two kinds—an experience of
facts, memories, emotions, body states—a thoroughly classical kind of
knowing which we might call "computer consciousness," which takes
place against a peculiar background of "raw awareness"—that uncanny
yet familiar feeling we relinquish when we go to sleep and awaken into
every morning. Some have called this second kind of experience "con-
sciousness without an object." I call it "ordinary awareness" and believe
that it is one human quality that distinguishes us from computers—at
least computers as they are presently constituted.

If ordinary awareness is a direct connection to quantum reality, then
just as our external knowledge of quantum entities may be characterized
by the term "quantum ignorance," so we might call this immediate inter-
nal experience of the world's real nature "quantum knowledge." One of
the greatest scientific achievements imaginable would be the discovery of
an explicit relationship between the waveform alphabets of quantum the-
ory and certain human states of consciousness.

Bell's theorem shows that although the world's phenomena seem
strictly local, the reality beneath this phenomenal surface must be superlu-
minal. The world's deep reality is maintained by an invisible quantum
connection whose ubiquitous influence is unmediated, unmitigated, and
immediate. Unconfirmed rumors of telepathy and other alleged powers of
mind aside, our basic computer consciousness appears to be as local as any
other classical phenomenon. However, if ordinary awareness is a private
manifestation of deep quantum reality, Bell's theorem requires our quan-
tum knowledge to be non-local, instantly linked to everything it has previ-
ously touched. Since this type of awareness consists of consciousness with-
out content, it is difficult to see what use we could make of such non-local

connections. On the other hand, perhaps these connections are not there
for us to "use."

Religions assure us that we are all brothers and sisters, children of the
same deity; biologists say that we are entwined with all life-forms on this
planet: our fortunes rise or fall with theirs. Now, physicists have discov-
ered that the very atoms of our bodies are woven out of a common super-
luminal fabric. Not merely in physics are humans out of touch with real-
ity; we ignore these connections at our peril. Albert Einstein, a seeker
after reality all his life, had this to say concerning the illusion of separate-

ness:

"A human being is part of the whole, called by us 'Universe'; a part
limited in time and space. He experiences himself, his thoughts and feel-
ings as something separated from the rest—a kind of optical delusion of
his consciousness. This delusion is a kind of prison for us, restricting us to
our personal desires and to affection for a few persons nearest us. Our task
must be to free ourselves from this prison by widening our circle of com-
passion to embrace all living creatures and the whole of nature in its
beauty. Nobody is able to achieve this completely but the striving for such
achievement is, in itself, a part of the liberation and a foundation for inner
security."

APPENDIX I -

Additional Readings on
Quantum Reality

The following list of books and articles on the quantum reality question is not
meant to be complete but represents material I have found useful in making sense
of this field.

General References

1.  Foundations of Quantum Mechanics: Proceedings of the International School
of Physics "Enrico Fermi" Course 49, Bernard d'Espagnat ed. New York:
Academic Press (1971).

2.   The Philosophy of Quantum Mechanics, Max Jammer. New York: Wiley
(1974).

3.   Conceptual Foundations of Quantum Mechanics (Second Edition), Bernard
d'Espagnat. Reading, Mass.: W. A. Benjamin (1976).

4.  Quantum Theory and Measurement, John Archibald Wheeler & Wojciech
Hubert Zurek eds. Princeton, N.J.: Princeton University Press (1983).

These four books are essential reading for serious reality researchers. Reference
# 1 is a record of a summer school on quantum foundations; Reference # 2 is a
detailed historical review of the quantum reality question. The book by d'Espagnat
is the nearest thing to a textbook in this field. Reference #4 is a collection of
important articles on quantum reality research; articles cited here that are also
reprinted in the Wheeler-Zurek collection are marked with an asterisk.

Specific Quantum Realities

5.  Atomic Physics and Human Knowledge, Niels Bohr. New York: Wiley (1963).

6.   "The Copenhagen Interpretation," Henry Stapp. American Journal of Physics
40 1098 (1972).

7.  "Law Without Law" (*), John Archibald Wheeler (see Wheeler & Zurek,
Ref. #4, p. 182).

8.   Wholeness and the Implicate Order, David Bohm. London: Routledge and
Kegan Paul (1980).

9.   The Many- Worlds Interpretation of Quantum Mechanics, Bryce DeWitt & R.
Neill Graham. Princeton, N.J.: Princeton University Press (1973).

10.   "The Logic of Quantum Physics," David Finkelstein. Transactions of the NY
Academy of Sciences 25 #6 621 (1965).

11.   "Quantum Logic," Carl G. Adler & James F. Wirth. American Journal of
Physics 51 412 (1983).

12.   "Remarks on the Mind-body Question" (*) in The Scientist Speculates, I. J.
Good, ed.; New York: Basic Books (1962).

13.   "Mind, Matter and Quantum Mechanics," Henry P. Stapp. Foundations of
Physics 12 363 (1982).

14.  A Survey of Hidden-Variables Theories, Frederik J. Belinfante. Oxford: Per-
gamon Press (1973).

15.   "Measurement Understood through the Quantum Potential Approach,"
David Bohm and Basil Hiley. Foundations of Physics 14 255 (1984).

16.  Physics and Philosophy, Werner Heisenberg. New York: Harper & Brothers
(1958).

These are the best references I can recommend on the eight quantum realities
described in the text.

Textbooks of Particular Interest

17.  Mathematical Foundations of Quantum Mechanics (English translation by
R. T. Beyer), John von Neumann. Princeton, N.J.: Princeton (1955).

18.  Quantum Theory, David Bohm. New York: Prentice-Hall (1951).

19.   The Feynman Lectures on Physics: Volume III, Richard P. Feynman, Robert
B. Leighton, Matthew Sands. Reading, Mass.: Addison-Wesley (1965).

20.  Quantum Mechanics and Path Integrals, R. P. Feynman and A. R. Hibbs.
New York: McGraw-Hill (1965).

Reference # 17 is von Neumann's "quantum bible"—the mathematical frame-
work which still holds up quantum theory. Bohm's textbook is a clear presentation
of quantum theory from the Copenhagen standpoint written before his defection
to the neorealist camp. Reference # 19 is an unusually lucid introduction to this

theory. In Reference # 20, Feynman describes his sum-over-histories approach in
considerable detail.

The EPR Paradox and Bell's Theorem

21.  "Can Quantum-mechanical Description of Physical Reality Be Considered
Complete?" (*), Albert Einstein, Boris Podolsky, Nathan Rosen. Physical Re-
view 47 777 (1935).

22.  "Can Quantum-mechanical Description of Physical Reality Be Considered
Complete?" (*), Niels Bohr. Physical Review 48 696 (1935).

23.  "On the Problem of Hidden Variables in Quantum Mechanics" (*), John S.
Bell. Reviews of Modem Physics 38 447 (1966).

24.   "On the Einstein-Podolsky-Rosen Paradox" (*), John S. Bell. Physics 1 195
(1964).

25.   "Bell's Theorem: Experimental Tests and Implications," John F. Clauser and
Abner Shimony. Reports on Progress in Physics 41 1881 (1978).

26.   "Experimental Test of Bell's Inequalities Using Time-varying Analyzers," Al-
ain Aspect, Jean Dalibard, Gerard Roger. Physical Review Letters 49 1804
(1982).

Reference #21 is the original EPR paper and #22 is Bohr's reply. Reference
#23 is Bell's definitive analysis of von Neumann's proof and his premonitions of
Bell's theorem. Reference #24 is Bell's original formulation of his celebrated
theorem. The Clauser-Shimony article is a recent review of the experimental status
of Bell's theorem. The last paper is a description of Aspect's verification of Bell's
theorem using ultrafast polarization switches.

Special Topics

27.   The Ethereal Aether, Loyd S. Swenson, Jr. Austin: University of Texas (1972).

28.  Molecular Reality, Mary Jo Nye. New York: American Elsevier (1972).

29.   The Intensity Interferometer, Robert Hanbury Brown. New York: Halsted
Press (1974).

30.  "Quantum Non-Demolition Measurements" (*), V. B. Braginsky, Y. I.
Vorontsov, K. S. Thome. Science 209 547 (1980).

31.   "Squeezed States of Light," D. F. Walls. Nature 306 141 (1983).

The first two references chronicle the rise and fall of the luminiferous ether and
the ascent of the atomic hypothesis into indubitable reality status. The remaining
articles provide more details on the widths of photon proxy waves and the unusual
quantum attributes which are the subject of so-called QND measurements.

SUPERLUMINAL SIGNALING

32.  "FLASH—A Superluminal Communicator Based upon a New Kind of Quan-
tum Measurement," Nick Herbert. Foundations of Physics 12 1171 (1982).

33.   "Bell's Theorem and the Different Concepts of Locality," Philippe Eberhard.
Nuovo Cimento 46B 392 (1978).

34.  "A Single Quantum Cannot be Cloned," W. K. Wooters and W. H. Zurek.
Nature 299 802 (1982).

35.   "Is a Photon Amplifier Always Polarization Dependent?" L. Mandel. Nature
304 188 (1983).

Reference #32 is a typical proposal purporting to use quantum connectedness
to signal faster-than-light. Reference #33 contains Eberhard's proof that such
proposals must fail if quantum theory is correct and complete. References #34
and #35 supply the detailed refutation of this particular signaling scheme.

Popularizations of Quantum Reality Research

36.   The Tao of Physics, Fritjof Capra. Berkeley, Calif.: Shambhala (1975).

37.  Fabric of the Universe, Denis Postle. New York: Crown (1976).

38.   The Dancing Wu Li Masters, Gary Zukav. New York: Morrow (1979).

39.   Other Worlds, Paul Davies. New York: Simon & Schuster (1980).

40.   Taking the Quantum Leap, Fred Alan Wolf. New York: Harper & Row
(1981).

41.   The Cosmic Code, Heinz R. Pagels. Simon & Schuster (1982).

42.  In Search of Reality, Bernard d'Espagnat. Berlin, West Germany: Springer-
Verlag(1983).

43.   The Quantum World, J. C. Polkinghorne. Harlow, Essex, England: Longman
(1984).

44.  In Search of Schrodinger's Cat, John Gribbin. New York: Bantam (1984).

These presentations of the quantum reality question illustrate the divergent and
contradictory views of physicists (and their interpreters) concerning the nature of
deep reality. Of particular interest is Pagels' "reality marketplace" in Reference

#41.

Articles on Quantum Reality

45.  "Quantum Mechanics and Reality," Bryce DeWitt. Physics Today 23 p. 30
September (1970).

46.  "Quantum Theory and Reality," Bernard d'Espagnat. Scientific American 241
p. 158 November (1979).

47.  "Ghostly Interactions in Physics," Basil Hiley. New Scientist p. 746 March 6
(1980).

48.  "Physicists Redefine Reality." London Economist p. 95 September 26 (1981).

49.   "Quantum Mysteries for Everyone," N. David Mermin. Journal of Philosophy
78 397 (1981).

50.  "Quantum Weirdness," Martin Gardner. Discover 3 #10 69 (1982).

51.   "Quantum Mechanics Passes Another Test," Arthur L. Robinson. Science
217 435 (1982).

52.   "Loophole Closed in Quantum Mechanics Test," Arthur L. Robinson. Sci-
ence 2/9 40 (1983).

53.   "Facing Quantum Mechanical Reality," Fritz Rohrlich. Science 221 1251
(1983).

These articles are mainly for the benefit of scientists working in fields other than
quantum reality research or for the general public. The report on scientists' redefi-
nition of reality (Reference #48) in the London Economist appears to have made
no impact whatsoever on the world's financial reality.

Direct Experience

54.  Reality and Empathy, Alex Comfort. Albany: State University of New York
(1984).

55.   The Sex Sphere, Rudy Rucker. New York: Ace Science Fiction (1983).

56.  Mr. Tompkins in Paperback, George Gamow. Cambridge, England: Cam-
bridge University Press (1965).

57.   Cosmicomics, Italo Calvino. New York: Harcourt, Brace & World (1968).

58.  All the Myriad Ways, Larry Niven. New York: Ballantine (1971).

59.  Bell's Book, Helen Luster. Fur Line Press (1976): available from Manroot
Books, Box 982, South San Francisco, CA 94080.

60.  Schmdinger's Cat, Robert Anton Wilson. New York: Pocket Books (1981).

61.  Superluminal, Vonda Mclntyre. Boston: Houghton Mifflin (1983).

Delving into the mysteries of everyday experience, Alex (joy of Sex) Comfort
interviews the demon "Gezumpstein" who can perceive the world "as it really is."
Rudy Rucker's like-minded demon calls herself "Babsi."

In Mr. Tompkins' world, new values for the physical constants make quantum
and relativity effects part of everyday life. Professor Gamow I'm sure meant these
imaginary worlds to be taken with a grain of salt, not as serious pictures of quan-
tum reality. Cosmicomics explores what a consciousness-centered cosmos might
feel like from the inside. Niven's story describes some unexpected psychological
consequences of the many-worlds reality. Using poetic reverie as probe, Luster's
Bell's Book tests our linguistic safety net for irregular connections. Various quan-
tum realities form the backdrop for Wilson's wacky freak show. In Mclntyre's
Superluminal, the achievement of faster-than-light travel opens up new space-time
possibilities for humankind.