X. COSMOGONIC SPECULATIONS FOUNDED ON TIDAL FRICTION (cont.)
51. The Other Planetary Sub-Systems
If this has been the evolution of the earth and moon, a similar process must have been going on elsewhere. So far we have only considered a single satellite and the sun, but the theory may of course be extended, with modifications, to planets attended by several satellites. We will now, therefore, consider some of the other members of the solar system. A large planet has much more energy of rotation to be destroyed, and moment of momentum to be redistributed, than a small one, and therefore a large planet ought to proceed in its evolution more slowly than a small one. Therefore we ought to find the larger planets less advanced than the smaller ones. The masses of such of the planets as have satellites are, in terms of the earth’s mass, as follows:—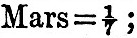 Jupiter=340; Saturn=100; Uranus=l7; Neptune=20.
Jupiter=340; Saturn=100; Uranus=l7; Neptune=20.
Mars should therefore be furthest advanced in its evolution, and it is here alone in the whole system that we find a satellite moving orbitally faster than the planet rotates. This will also be the ultimate fate of our moon, because, after its orbital motion has been reduced to identity with that of the earth’s rotation, solar tidal friction will further reduce the earth’s angular velocity; the tidal reaction on the moon will then be reversed, and the moon’s orbital velocity will increase and her distance from the earth diminish. But, since the moon’s mass is very large, she must recede to an enormous distance from the earth before this reversal takes place. Now the satellites of Mars are very small, and therefore they need only recede a very short distance from the planet before the reversal of tidal reaction. The periodic time of the satellite Deimos is 30h 18m, and, as the period of rotation of Mars is 24h 37m, Deimos must be still receding from Mars, but very slowly. The periodic time of the satellite Phobos is 7h 39m; therefore it must be approaching Mars. It does not seem likely that it has ever been remote from the planet. [Footnote 379-1] The eccentricities of the orbits of both satellites are small: that of Deimos is ·0057 and that of Phobos ·0066. If the viscosity of the planet be small, or if oceanic tidal friction be the principal cause of change, both eccentricities are diminishing; but, if the viscosity be large, both are increasing. As we have no means of knowing whether the eccentricities are increasing or diminishing, the larger eccentricity of the orbit of Phobos cannot be a fact of much importance either for or against the present views. But it must be admitted that it is a slightly unfavourable indication. The position of the proper plane of a satellite is determined by the periodic time of the satellite, the oblateness of the planet, and the sun’s distance. The inclination of the orbit of a satellite to the proper plane is not determined by anything in the system. Hence it is only the inclination of the orbit which can afford any argument for or against the theory. The proper planes of both satellites are necessarily nearly coincident with the equator of the planet; but it is in accordance with the theory that the inclinations of the orbits to their respective proper planes should be small. Any change in the obliquity of the equator of Mars to the plane of his orbit must be entirely due to solar tides. The present obliquity is about 30°, and this points also to an advanced stage of evolution, at least if the axis of the planet was primitively at all nearly perpendicular to the ecliptic.
We now come to the system of Jupiter. This enormous planet is still rotating in about ten hours; its axis is nearly perpendicular to the ecliptic; and three of its satellites revolve in seven days or less, whilst the fourth has a period of 16d 16h. This system is obviously far less advanced than our own. The inclinations of the proper planes to Jupiter’s equator are necessarily small, but the inclinations of the orbits to the proper planes appear to be very interesting from a theoretical point of view. They are in the case of the first satellite 0° 0″ 0′, in the case of the second 0° 27′ 50″, in that of the third 0° 12′ 20″, and in that of the fourth 0° 14″ 58′. We have shown above that the orbit of a satellite is first coincident with its proper plane, and that the inclination afterwards rises to a maximum and finally declines. If then we may assume, as seems reasonable, that the satellites are in stages of evolution corresponding to their distances from the planet, these inclinations accord well with the theory. The eccentricities of the orbits of the two inner satellites are insensible, those of the outer two small. This does not tell strongly either for or against the theory, because the history of the eccentricity depends considerably on the nature of the friction to which the tides are subject. Yet it on the whole agrees with the theory that the eccentricity should be greater in the more remote satellites. It appears that the satellites of Jupiter always present the same fare to the planet, just as does our moon. This was to be expected.
The case of Saturn is not altogether so favourable to the theory. The extremely rapid rotation, the ring, and the short periodic time of the inner satellites point to an early stage of development; whilst the longer periodic time of the three outer satellites and the high obliquity of the equator indicate a later stage. Perhaps both views may be more or less correct, for successive shedding of satellites would impart a modern appearance to the system. It has probably been previously remarked that the Saturnian system bears a strong analogy to the solar system, Titan being analogous to Jupiter, Hyperion and Iapetus to Uranus and Neptune, and the inner satellites to the inner planets. Thus anything which aids us in forming a theory of the one system will throw light on the other. The details of the Saturnian system seem to be more or less favourable to the theory. The proper planes of the orbits except that of Iapetus) are nearly in the plane of the ring, and the inclinations of all the orbits thereto appear not to be large. As the result of a careful series of observations made at Washington in 1873, Prof. Asaph Hall [Footnote 380-1] finds that the eccentricities of the orbits of Mimas, Enceladus, Tethys, Dione, and Rhea are insensible, that of Titan is ·0284, of Hyperion ·1000, and that of Iapetus ·0278. The satellite Iapetus appears always to present the same face to the planet.
Concerning Uranus and Neptune there is not much to be said, as their systems are very little known; but their masses are much larger than that of the earth, and their satellites revolve with a short periodic time. The retrograde motion and high inclination of the satellites of Uranus are very remarkable. The theory of the inclination of the orbit has been based on an assumed smallness of inclination, and it is not very easy to see to what results investigation might lead if the inclination were large. It must be admitted, however, that the Uranian system points to the probability of the existence of a primitive planet, with retrograde rotation, or at least with a very large obliquity of equator.
It appears from this review that the other members of the solar system present some phenomena which are strikingly favourable to the tidal theory of evolution, and none which are absolutely condemnatory. We shall show in the following section that there are reasons why the tidal friction arising in the planetary systems cannot have had so much effect as in the case of the earth and moon. That the indications which we have just noted were not more marked, but yet seemed to exist, agrees well with this conclusion.
Footnote
379-1 Mr Nolan considers the theory inapplicable to the case of Mars; see Nature, 29th July 1886.
380-1 See Brit. Assoc. Report, 1886, p. 543.
Read the rest of this article:
Tides - Table of Contents